MATLAB现熵值法不确定性分析
一、基本原理
在信息论中,熵是对不确定性的一种度量。信息量越大,不确定性就越小,熵也就越小;信息量越小,不确定性越大,熵也越大。
根据熵的特性,可以通过计算熵值来判断一个事件的随机性及无序程度,也可以用熵值来判断某个指标的离散程度,指标的离散程度越大,该指标对综合评价的影响(权重)越大,其熵值越小。
二、熵值法步骤
1. 选取
n个国家,
m个指标,则
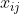 为第
i个国家的第
j个指标的数值(
i=1, 2…,
n;
j=1,2,…,
m);
为第
i个国家的第
j个指标的数值(
i=1, 2…,
n;
j=1,2,…,
m);
2. 指标的归一化处理:异质指标同质化
由于各项指标的计量单位并不统一,因此在用它们计算综合指标前,先要对它们进行标准化处理,即把指标的绝对值转化为相对值,并令 ,从而解决各项不同质指标值的同质化问题。而且,由于正向指标和负向指标数值代表的含义不同(正向指标数值越高越好,负向指标数值越低越好),因此,对于高低指标我们用不同的算法进行数据标准化处理。其具体方法如下:
正向指标:
负向指标:
则 为第
i个国家的第
j个指标的数值(
i=1, 2…,
n;
j=1, 2,…,
m)。为了方便起见,归一化后的数据仍记为
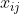 ;
;
3. 计算第
j项指标下第
i个国家占该指标的比重:
4. 计算第
j项指标的熵值:
其中
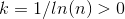 . 满足
. 满足
 ;
;
5. 计算信息熵冗余度:
6. 计算各项指标的权值:
7. 计算各国家的综合得分:
注:对正逆指标归一化的时候如果采用的方法不一样,正指标归一化得到的值会大一些,逆指标的归一化得到的值会小一些,然后算权重,逆指标对应的权重也会相应的小,从而逆指标对应的得分也小些,就相当于对逆指标进行了处理。如果对正逆指标归一化采用的方法一样,为了体现逆指标的不利影响,最后应该总分减去逆指标的得分的。两种方法不同,但都是为了体现逆指标对综合得分的不利影响。
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
[code]
function [s,w]=shang(x)
% 函数shang.m, 实现用熵值法求各指标(列)的权重及各数据行的得分
% x为原始数据矩阵, 一行代表一个国家, 每列对应一个指标
% s返回各行得分, w返回各列权重
[n,m]=size(x); % n=23个国家, m=5个指标
%% 数据的归一化处理
% Matlab2010b,2011a,b版本都有bug,需如下处理. 其它版本直接用[X,ps]=mapminmax(x',0,1);即可
[X,ps]=mapminmax(x');
ps.ymin=0.002; % 归一化后的最小值
ps.ymax=0.996; % 归一化后的最大值
ps.yrange=ps.ymax-ps.ymin; % 归一化后的极差,若不调整该值, 则逆运算会出错
X=mapminmax(x',ps);
% mapminmax('reverse',xx,ps); % 反归一化, 回到原数据
X=X'; % X为归一化后的数据, 23行(国家), 5列(指标)
%% 计算第j个指标下,第i个记录占该指标的比重p(i,j)
for i=1:n
for j=1:m
p(i,j)=X(i,j)/sum(X(:,j));
end
end
%% 计算第j个指标的熵值e(j)
k=1/log(n);
for j=1:m
e(j)=-k*sum(p(:,j).*log(p(:,j)));
end
d=ones(1,m)-e; % 计算信息熵冗余度
w=d./sum(d); % 求权值w
s=w*p'; % 求综合得分
[\code]
测试程序:
data.txt 数据如下:
114.6 1.1 0.71 85.0 346
55.3 0.96 0.4 69.0 300
132.4 0.97 0.54 73.0 410
152.1 1.04 0.49 77.0 433
103.5 0.96 0.66 67.0 385
81.0 1.08 0.54 96.0 336
179.3 0.88 0.59 89.0 446
29.8 0.83 0.49 120.0 289
92.7 1.15 0.44 154.0 300
248.6 0.79 0.5 147.0 483
115.0 0.74 0.65 252.0 453
64.9 0.59 0.5 167.0 402
163.6 0.85 0.58 220.0 495
95.7 1.02 0.48 160.0 384
139.5 0.70 0.59 217.0 478
89.9 0.96 0.39 105.0 314
76.7 0.95 0.51 162.0 341
121.8 0.83 0.60 140.0 401
42.1 1.08 0.47 110.0 326
78.5 0.89 0.44 94.0 280
77.8 1.19 0.57 91.0 364
90.0 0.95 0.43 89.0 301
100.6 0.82 0.59 83.0 456
执行代码:
[code] x=load('data.txt'); % 读入数据
data.txt 数据如下:
114.6 1.1 0.71 85.0 346
55.3 0.96 0.4 69.0 300
132.4 0.97 0.54 73.0 410
152.1 1.04 0.49 77.0 433
103.5 0.96 0.66 67.0 385
81.0 1.08 0.54 96.0 336
179.3 0.88 0.59 89.0 446
29.8 0.83 0.49 120.0 289
92.7 1.15 0.44 154.0 300
248.6 0.79 0.5 147.0 483
115.0 0.74 0.65 252.0 453
64.9 0.59 0.5 167.0 402
163.6 0.85 0.58 220.0 495
95.7 1.02 0.48 160.0 384
139.5 0.70 0.59 217.0 478
89.9 0.96 0.39 105.0 314
76.7 0.95 0.51 162.0 341
121.8 0.83 0.60 140.0 401
42.1 1.08 0.47 110.0 326
78.5 0.89 0.44 94.0 280
77.8 1.19 0.57 91.0 364
90.0 0.95 0.43 89.0 301
100.6 0.82 0.59 83.0 456
执行代码:
[code] x=load('data.txt'); % 读入数据
[s,w]=shang(x)
[\code]
运行结果:
s =
Columns 1 through 9
0.0431 0.0103 0.0371 0.0404 0.0369 0.0322 0.0507 0.0229 0.0397
Columns 10 through 18
0.0693 0.0878 0.0466 0.0860 0.0503 0.0800 0.0234 0.0456 0.0536
Columns 19 through 23
0.0272 0.0181 0.0364 0.0202 0.0420
w =
0.1660 0.0981 0.1757 0.3348 0.2254
转自:http://www.ilovematlab.cn/thread-452528-1-1.html