逐点比较直线插补和圆弧插补
对于只在第一象限的各种插补方式,都比较的简单。
逐点比较直线插补
由于我们将直线的起点平移到了原点,那么我们所比较的就是当前点和目标直线的斜率,当在直线下方,y++;
当在直线上方,x++;
当在直线上,规定x++;
设(xm,ym)为当前点,(xe,ye)为终点
则Fm=ymxe-xmye可表示点在直线的位置。
Fm=0,点在直线上;
Fm>0,点在直线上方;
Fm<0,点在直线下方;
于是当Fm≥0时,x++;
Fm<0时,y++;
如果每次都计算Fm=ymxe-xmye运算时间比较长,我们可以通过xm=xm+1,ym=ym+1来简化运算;
于是Fm≥0时,Fm-=ye;
Fm<0,Fm+=xe;
由此因为起始点为0,所以Fm=0,然后根据上述规则进行步进。c++代码如下
void go()
{
int xe, ye;
int xs, ys;
queue<int>a;//表示往哪里走
queue<int>Fm;//标记Fm
cout << "请输入初始点" << endl;
cin >> xs >> ys;
cout << "请输入终止点" << endl;
cin >> xe >> ye;
cout << "输入结束,下面开始进行计算" << endl;
int fm = 0;
Fm.push(fm);
int NXY = xe - xs + ye - ys;
for (int i = 0; i < NXY; i++)
{
if (fm >= 0)
{
fm -= ye;
a.push(1);
Fm.push(fm);
}
else
{
fm += xe;
a.push(3);
Fm.push(fm);
}
}
for (int i = 0; i <= NXY; i++)
{
cout << Fm.front() << endl;
Fm.pop();
}
int mx = 100;
int my = 300;
int length = 30;
int flag = 0;
initgraph(640, 480);
setlinecolor(BLUE);
line(mx, my, mx + length * xe, my - length * ye);
setlinecolor(WHITE);
line(mx - 90, my, mx + 240, my);
line(mx, my + 90, mx, my - 240);
setlinecolor(RED);
for (int i = 0; i < NXY; i++)
{
flag = a.front();
a.pop();
jiantou(mx, my, flag, length, i);
}
//closegraph();
_getch();
}
逐点比较圆弧插补
同样的,对于直线而言,比较斜率;那么对于圆弧来说比较的是到圆心的距离。
这里我们都是需要将圆心平移到坐标原点。
这里我们讨论逆圆弧。
假设初始点为xm,ym;终止点为xe,ye。
那么半径R^2 = xe^2 + ye^2
定义Fm=xm^2 + ym^2 - R^2
如果Fm≥0,那么xm–;
Fm<0,ym++;
将上述带到Fm表达式可得:
Fm≥0,Fm+=1-2xm;
Fm<0,Fm+=1+2ym;
c++程序如下:
void go2()
{
int xe, ye;
int xs, ys;
int xm, ym;
queue<int>a;//表示往哪里走
queue<int>Fm;//标记Fm
cout << "请输入初始点" << endl;
cin >> xs >> ys;
cout << "请输入终止点" << endl;
cin >> xe >> ye;
cout << "输入结束,下面开始进行计算" << endl;
xm = xs;
ym = ys;
int fm = 0;
Fm.push(fm);
int NXY = abs(xe - xs) + abs(ye - ys);
for (int i = 0; i < NXY; i++)
{
if (fm >= 0)
{
fm += 1 - 2 * xm;
a.push(2);
Fm.push(fm);
xm--;
}
else
{
fm += 1 + 2 * ym;
a.push(3);
Fm.push(fm);
ym++;
}
}
for (int i = 0; i <= NXY; i++)
{
cout << Fm.front() << endl;
Fm.pop();
}
int mx = 300;
int my = 300;
int length = 30;
int flag = 0;
initgraph(640, 480);
setlinecolor(BLUE);
circle(mx, my, length * sqrt(xe * xe + ye * ye));
setlinecolor(WHITE);
line(mx - length * sqrt(xe * xe + ye * ye), my, mx + length * sqrt(xe * xe + ye * ye), my);
line(mx , my+length * sqrt(xe * xe + ye * ye), mx , my-length * sqrt(xe * xe + ye * ye));
setlinecolor(RED);
mx += xs * length;
my -= ys * length;
for (int i = 0; i < NXY; i++)
{
flag = a.front();
a.pop();
jiantou(mx, my, flag, length, i);
}
_getch();
closegraph();
}
这里给出画图的走步程序
void jiantou(int& x1, int& y1, int flag, int length, int i)
{
TCHAR A[5];
swprintf_s(A, _T("%d"), i+1);
int x2, y2;
if (flag == 1)//+x
{
x2 = x1 + length;
y2 = y1;
line(x1, y1, x2, y2);
line(x2 - 7, y2 - 7, x2, y2);
line(x2 - 7, y2 + 7, x2, y2);
outtextxy((x1 + x2) / 2, y1 - 6,A);
x1 = x2;
y1 = y2;
}
else if (flag == 2)//-x
{
x2 = x1 - length;
y2 = y1;
line(x1, y1, x2, y2);
line(x2 + 7, y2 - 7, x2, y2);
line(x2 + 7, y2 + 7, x2, y2);
outtextxy((x1 + x2) / 2, y1 - 6, A);
x1 = x2;
y1 = y2;
}
else if (flag == 3)//+y
{
x2 = x1;
y2 = y1 - length;
line(x1, y1, x2, y2);
line(x2 - 7, y2 + 7, x2, y2);
line(x2 + 7, y2 + 7, x2, y2);
outtextxy(x2 + 6, (y1 + y2) / 2, A);
x1 = x2;
y1 = y2;
}
else if (flag == 4)//-y
{
x2 = x1;
y2 = y1 + length;
line(x1, y1, x2, y2);
line(x2 - 7, y2 - 7, x2, y2);
line(x2 + 7, y2 - 7, x2, y2);
x1 = x2;
y1 = y2;
}
}
结果如下:
直线插补起点(0,0),终点(5,3)
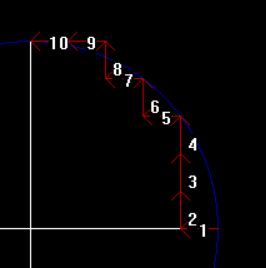
 逆圆弧插补起点(5,0),终点(0,5)
逆圆弧插补起点(5,0),终点(0,5)
全部程序如下
#include