K-L变换实现图像压缩
卡洛南-洛伊(karhunen-Loeve)变换,简称K-L变换,也叫霍特林变换或者主成分分析。
必备数学知识:协方差,相关系数,协方差矩阵(这三个知识点我是参考的同济大学的概率论数与数理统计那本书,讲的很实在),对称矩阵相似对角化
协方差与相关系数都是用来衡量不同维度之间的相关性,正值越大说明正相关越高,负值越大说明负相关越高。协方差在matlab中可用cov()来进行计算,如下图

**主对角线的值代表了方差,其余的就代表了协方差。
matlab中corrcoef是计算的各维度之间的相关系数,就是在协方差基础上除以标准差来归一化**

我们看到主对角线都为1,说明方差为1
K-L变换

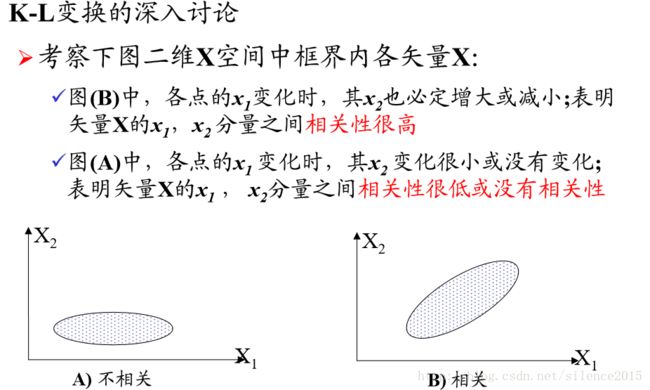
K-L变换的实质就是去除各维度之间的相关性。就是建立新的坐标系,将原本高度相关的数据在新坐标系下的协方差矩阵除对角线以外的元素都是零。如图:

在原坐标系下的x,y具有很强的相关性,y大致随着x的增大而增大。但在新坐标系下(x’,y’坐标系),横纵 坐标之间变得没有相关性,这表明相关性被去除。

如何实现坐标转换
构建新坐标系的过程就是主成分变换的过程。y代表新坐标系的坐标点,x代表原来坐标系的点。
y=G∗x
其中G就是变换矩阵,G矩阵就是x的协方差矩阵的特征向量矩阵的转置矩阵。
Σx代表x的协方差矩阵
λi代表Σx的特征值,ξi代表λi的特征向量
matrix=[ξ1,ξ2,ξ3.......ξn]代表由协方差矩阵的特征向量组成的矩阵
G=matrixT
其实求解变换矩阵G就是求使得对阵矩阵相似对角化的正交矩阵P
因为Σx协方差矩阵是一个实对称矩阵,欲消除各维度的相关性也就是要使得将该矩阵转换成对角矩阵

K-L变换示例
1、读取一幅图像,f图像的size为359*479
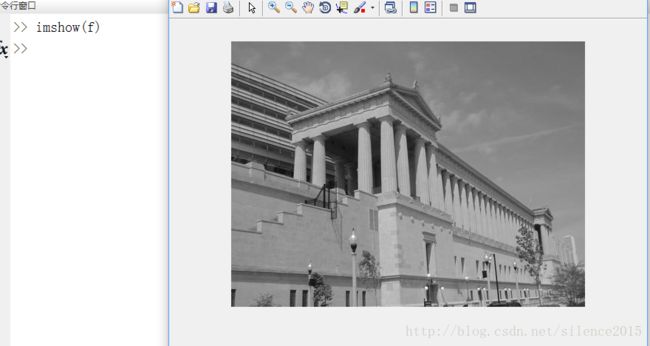
2、matlab函数princomp()可以方便计算特征矩阵向量coeff,和特征值latent
[coeff,score,latent]=princomp(f);
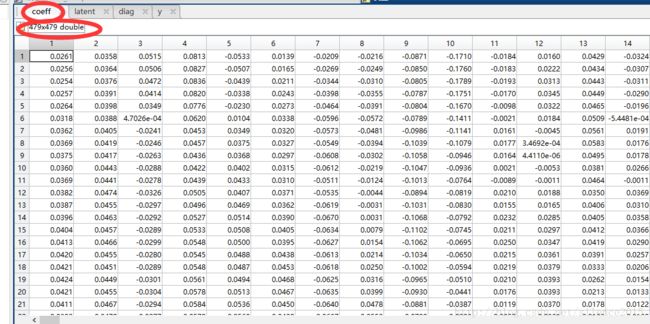

3、将原图像转换到新坐标系下
y=f∗ceoff
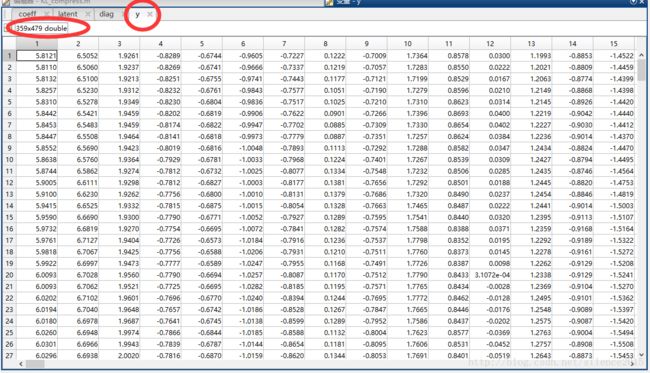
可以发现,转换后的图像越往后的列的值越小,可以用图像更直观地看
将部分很小的y值置零
y(:,200:end)=0;
再将图像复原
yi=y∗coeff′;
复原的图像如下显示

观察得到,图像有损失,但是存储压力小很多。
matlab图像压缩
function KL_compress(imgpath)
% 使用K-L变换/主成分分析来对图像压缩
f=imread(imgpath);
f=im2double(f);
y=[];
[m,n]=size(f);
% 拆分图像,将8*8的图像小块展开成1*64的向量,K-L变换的变换矩阵只和维度有关,故只需64*64的变换矩阵就可以了
% 虽然这样计算降低了计算复杂度 ,但是并没有消除小块之间的相关性,但实验结果表明效果良好
for i=1:m/8
for j=1:n/8
ii=(i-1)*8+1;
jj=(j-1)*8+1;
y_append=reshape(f(ii:ii+7,jj:jj+7),1,64) % 将图像分成8*8的小块
y=[y;y_append];
end
end
% K-L变换
[coeff,score,latent]=princomp(y);
k1=y*coeff;
k11=k1;
k12=k1;
k13=k1;
% 置0压缩过程
k11(:,33:64)=0;
k12(:,17:64)=0;
k13(:,9:64)=0;
% K-L逆变换
k11_inverse=k11*coeff';
k12_inverse=k12*coeff';
k13_inverse=k13*coeff';
k=1;
% 重组图像
for i=1:m/8
for j=1:n/8
y1=reshape(k11_inverse(k,1:64),8,8);
y2=reshape(k12_inverse(k,1:64),8,8);
y3=reshape(k13_inverse(k,1:64),8,8);
ii=(i-1)*8+1;
jj=(j-1)*8+1;
image1(ii:ii+7,jj:jj+7)=y1;
image2(ii:ii+7,jj:jj+7)=y2;
image3(ii:ii+7,jj:jj+7)=y3;
k=k+1;
end
end
imshow(image1),title('压缩50%');
figure,imshow(image2),title('压缩73%');
figure,imshow(image3),title('压缩86%');
end