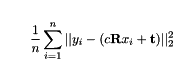《PCL点云库学习&VS2010(X64)》Part 34 旋转平移矩阵用法

《PCL点云库学习&VS2010(X64)》Part 34 旋转平移矩阵用法

1、变换与投影矩阵讲解：

https://en.wikipedia.org/wiki/Transformation_matrix

http://web.iitd.ac.in/~hegde/cad/lecture/L6_3dtrans.pdf

点云变换主要涉及平移、旋转、缩放、反射、剪切、视角转换、投影等，这里主要介绍平移与旋转。

2、使用Eigen::Matrix4f 进行变换

#include 
#include 
#include 

int
main(int argc, char** argv)
{
	// Objects for storing the point clouds.
	pcl::PointCloud::Ptr cloud(new pcl::PointCloud);
	pcl::PointCloud::Ptr transformed(new pcl::PointCloud);

	// Read a PCD file from disk.
	if (pcl::io::loadPCDFile(argv[1], *cloud) != 0)
	{
		return -1;
	}

	// Transformation matrix object, initialized to the identity matrix
	// (a null transformation).
	Eigen::Matrix4f transformation = Eigen::Matrix4f::Identity();

	// Set a rotation around the Z axis (right hand rule).
	float theta = 90.0f * (M_PI / 180.0f); // 90 degrees.
	transformation(0, 0) = cos(theta);
	transformation(0, 1) = -sin(theta);
	transformation(1, 0) = sin(theta);
	transformation(1, 1) = cos(theta);

	// Set a translation on the X axis.
	transformation(0, 3) = 1.0f; // 1 meter (positive direction).

	pcl::transformPointCloud(*cloud, *transformed, transformation);

	// Visualize both the original and the result.
	pcl::visualization::PCLVisualizer viewer(argv[1]);
	viewer.addPointCloud(cloud, "original");
	// The transformed one's points will be red in color.
	pcl::visualization::PointCloudColorHandlerCustom colorHandler(transformed, 255, 0, 0);
	viewer.addPointCloud(transformed, colorHandler, "transformed");
	// Add 3D colored axes to help see the transformation.
	viewer.addCoordinateSystem(1.0, 0);

	while (!viewer.wasStopped())
	{
		viewer.spinOnce();
	}
}

2、使用Eigen::Affine3进行变换

#include 

#include 
#include 
#include 
#include 
#include 
#include 

// This function displays the help
void
showHelp(char * program_name)
{
  std::cout << std::endl;
  std::cout << "Usage: " << program_name << " cloud_filename.[pcd|ply]" << std::endl;
  std::cout << "-h:  Show this help." << std::endl;
}

// This is the main function
int
main (int argc, char** argv)
{

  // Show help
  if (pcl::console::find_switch (argc, argv, "-h") || pcl::console::find_switch (argc, argv, "--help")) {
    showHelp (argv[0]);
    return 0;
  }

  // Fetch point cloud filename in arguments | Works with PCD and PLY files
  std::vector filenames;
  bool file_is_pcd = false;

  filenames = pcl::console::parse_file_extension_argument (argc, argv, ".ply");

  if (filenames.size () != 1)  {
    filenames = pcl::console::parse_file_extension_argument (argc, argv, ".pcd");

    if (filenames.size () != 1) {
      showHelp (argv[0]);
      return -1;
    } else {
      file_is_pcd = true;
    }
  }

  // Load file | Works with PCD and PLY files
  pcl::PointCloud::Ptr source_cloud (new pcl::PointCloud ());

  if (file_is_pcd) {
    if (pcl::io::loadPCDFile (argv[filenames[0]], *source_cloud) < 0)  {
      std::cout << "Error loading point cloud " << argv[filenames[0]] << std::endl << std::endl;
      showHelp (argv[0]);
      return -1;
    }
  } else {
    if (pcl::io::loadPLYFile (argv[filenames[0]], *source_cloud) < 0)  {
      std::cout << "Error loading point cloud " << argv[filenames[0]] << std::endl << std::endl;
      showHelp (argv[0]);
      return -1;
    }
  }

  /* Reminder: how transformation matrices work :

           |-------> This column is the translation
    | 1 0 0 x |  \
    | 0 1 0 y |   }-> The identity 3x3 matrix (no rotation) on the left
    | 0 0 1 z |  /
    | 0 0 0 1 |    -> We do not use this line (and it has to stay 0,0,0,1)

    METHOD #1: Using a Matrix4f
    This is the "manual" method, perfect to understand but error prone !
  */
  Eigen::Matrix4f transform_1 = Eigen::Matrix4f::Identity();

  // Define a rotation matrix (see https://en.wikipedia.org/wiki/Rotation_matrix)
  float theta = M_PI/4; // The angle of rotation in radians
  transform_1 (0,0) = cos (theta);
  transform_1 (0,1) = -sin(theta);
  transform_1 (1,0) = sin (theta);
  transform_1 (1,1) = cos (theta);
  //    (row, column)

  // Define a translation of 2.5 meters on the x axis.
  transform_1 (0,3) = 2.5;

  // Print the transformation
  printf ("Method #1: using a Matrix4f\n");
  std::cout << transform_1 << std::endl;

  /*  METHOD #2: Using a Affine3f
    This method is easier and less error prone
  */
  Eigen::Affine3f transform_2 = Eigen::Affine3f::Identity();

  // Define a translation of 2.5 meters on the x axis.
  transform_2.translation() << 2.5, 0.0, 0.0;

  // The same rotation matrix as before; theta radians arround Z axis
  transform_2.rotate (Eigen::AngleAxisf (theta, Eigen::Vector3f::UnitZ()));

  // Print the transformation
  printf ("\nMethod #2: using an Affine3f\n");
  std::cout << transform_2.matrix() << std::endl;

  // Executing the transformation
  pcl::PointCloud::Ptr transformed_cloud (new pcl::PointCloud ());
  // You can either apply transform_1 or transform_2; they are the same
  pcl::transformPointCloud (*source_cloud, *transformed_cloud, transform_2);

  // Visualization
  printf(  "\nPoint cloud colors :  white  = original point cloud\n"
      "                        red  = transformed point cloud\n");
  pcl::visualization::PCLVisualizer viewer ("Matrix transformation example");

   // Define R,G,B colors for the point cloud
  pcl::visualization::PointCloudColorHandlerCustom source_cloud_color_handler (source_cloud, 255, 255, 255);
  // We add the point cloud to the viewer and pass the color handler
  viewer.addPointCloud (source_cloud, source_cloud_color_handler, "original_cloud");

  pcl::visualization::PointCloudColorHandlerCustom transformed_cloud_color_handler (transformed_cloud, 230, 20, 20); // Red
  viewer.addPointCloud (transformed_cloud, transformed_cloud_color_handler, "transformed_cloud");

  viewer.addCoordinateSystem (1.0, "cloud", 0);
  viewer.setBackgroundColor(0.05, 0.05, 0.05, 0); // Setting background to a dark grey
  viewer.setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 2, "original_cloud");
  viewer.setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 2, "transformed_cloud");
  //viewer.setPosition(800, 400); // Setting visualiser window position

  while (!viewer.wasStopped ()) { // Display the visualiser until 'q' key is pressed
    viewer.spinOnce ();
  }

  return 0;
}

3、使用Eigen::Quaternion

4、总结：

1）使最小二乘方程值最小，从而求得c,R,T三个参数，分别表示局部放大系数、旋转系数和平移系数。

齐次变换后得到一个4x4矩阵：

返回一个矩阵，使上述的最小二乘方程最小。

见文章“Least-squares estimation of transformation parameters between two point patterns”Shinji Umeyama, PAMI 1991, DOI: 10.1109/34.88573

2）matrix4f的具体结构及意义。

  /* Reminder: how transformation matrices work :

           |-------> This column is the translation
    | 1 0 0 x |  \
    | 0 1 0 y |   }-> The identity 3x3 matrix (no rotation) on the left
    | 0 0 1 z |  /
    | 0 0 0 1 |    -> We do not use this line (and it has to stay 0,0,0,1)

    METHOD #1: Using a Matrix4f
    This is the "manual" method, perfect to understand but error prone !
  */

由上述的提示段代码可知，左上角的三行三列主要是旋转矩阵参数，最后一列的上三行是平移矩阵。

实际上该4x4矩阵肯定不止这些，具体的如下图所示：

其中p,q,r对应的透视变换参数，左上角三行三列包括局部缩放、剪切、旋转和反射等参数。具体的设置见文章中的第二个pdf链接。最后一行的l,m,n表示沿着x,y,z轴进行平移。s表示全局缩放参数。