数值分析——最佳平方逼近再分析
数值分析——最佳平方逼近再分析
- 理论
- 举例
- 连续型
- 基是 { 1 , x , . . . , x n } \{1,x,...,x^n\} {1,x,...,xn}型
- 基是任意由 { 1 , x , . . . , x n } \{1,x,...,x^n\} {1,x,...,xn}生成的正交多项式型
- 离散型
- 基是 { 1 , x , . . . , x n } \{1,x,...,x^n\} {1,x,...,xn}型(数学模型)
- 基是任意由 { 1 , x , . . . , x n } \{1,x,...,x^n\} {1,x,...,xn}生成的正交多项式型
- 课本答案
之前觉得逼近这个问题有些复杂,勒让德、切比雪夫正交多项式、数学建模……各种杂乱的东西混杂一团,遮蔽我们的双眼。再次研究了最佳平方逼近,下面讲一点我的理解,以为诸位揭开最佳平方逼近的本质。
理论
对于最佳平方逼近,有连续型的和离散型的两种。对应于连续型问题的逼近有两种情况,一是用基{1,x,…}逼近,二是用由基推出的正交多项式基逼近;而对于离散型问题,也有两种方法。不过离散型问题的正交多项式是由给出的离散点Xi推导。 不管是哪种逼近,整个问题的核心全在于公式

公式中, φ i \varphi_i φi, i = 0 , 1 , 2 , 3... n i=0,1,2,3...n i=0,1,2,3...n是我们给出的基。例如,如果基是 { 1 , x , x 2 . . . x n } \{1,x,x^2...x^n\} {1,x,x2...xn},那么 φ 0 = 1 , φ 1 = x \varphi_0=1,\varphi_1=x φ0=1,φ1=x。通过求解公式中的 a j a_j aj,我们能够找到一个由基线性组合成的函数 φ ∗ = ∑ a j φ j \varphi^*=\sum a_j\varphi_j φ∗=∑ajφj,这个函数就是我们的由平方逼近得到的逼近函数。OK,我们的故事讲完了,起飞。
你可能会惊了,那么多东西,就这就完了?? 是的,这就是我的学习风格,不喜欢记忆很多花里胡哨的,我只喜欢渗透本质,而这个公式,就是本质,不信你接着看。
举例
下面给出例子。我会把所有题的解析放在文章最末。
连续型
基是 { 1 , x , . . . , x n } \{1,x,...,x^n\} {1,x,...,xn}型
直接上书上例题。
例 : 设 f ( x ) = 1 + x 2 , 求 区 间 [ 0 , 1 ] 上 的 一 次 最 佳 平 方 逼 近 多 项 式 . 取 基 为 { 1 , x , . . . , x n } . 例:设f(x)=\sqrt{1+x^2},求区间[0,1]上的一次最佳平方逼近多项式.取基为\{1,x,...,x^n\}. 例:设f(x)=1+x2,求区间[0,1]上的一次最佳平方逼近多项式.取基为{1,x,...,xn}.
解:
我们主要讲思路,题解在文章最末看。那么,我们开始。首先我们要知道我们的目的是什么,这个非常重要,就像人活在世上要知道你要做什么一样。
首先明确基是什么? { 1 , x , . . . , x n } \{1,x,...,x^n\} {1,x,...,xn}。我们要求出什么? φ ∗ = ∑ a j φ j \varphi^*=\sum a_j\varphi_j φ∗=∑ajφj。由于题目需要我们的多项式次数为1,因此我们又要求出 a 0 , a 1 a_0,a_1 a0,a1。最终,我们的目的便是得到 φ ∗ = a 0 ∗ 1 + a 1 ∗ x \varphi^*=a_0*1+a_1*x φ∗=a0∗1+a1∗x。根据我们的公式便可以计算出。

即

这里函数内积的方式我就不再赘述了。在这个展开的公式里,我们知道什么? φ 0 , φ 1 \varphi_0,\varphi_1 φ0,φ1。 f f f是什么,这又是另外一个重点。再来一次,我们的目的是什么?更为原始的? 对了,用函数 φ ∗ = a 0 + a 1 x \varphi^*=a_0+a_1x φ∗=a0+a1x去逼近函数 f ( x ) = 1 + x 2 f(x)=\sqrt{1+x^2} f(x)=1+x2,所以 f f f就是我们的目标函数 ,OK,起飞。明确了这两点,这道题就只剩下算算算了。
基是任意由 { 1 , x , . . . , x n } \{1,x,...,x^n\} {1,x,...,xn}生成的正交多项式型
例 : 设 f ( x ) = exp ( x ) , 求 区 间 [ − 1 , 1 ] 上 的 L e g e n d r e 三 次 展 开 例:设f(x)=\exp(x),求区间[-1,1]上的Legendre三次展开 例:设f(x)=exp(x),求区间[−1,1]上的Legendre三次展开
解:
同样,清楚你的目的。问自己2个问题。
基是什么? L e g e n d r e 多 项 式 是 函 数 的 基 Legendre多项式是函数的基 Legendre多项式是函数的基,即

要求什么? φ ∗ = ∑ a j φ j \varphi^*=\sum a_j\varphi_j φ∗=∑ajφj,又题目让我们求三次 L e g e n d r e Legendre Legendre展开,因此我们最终的目的是求得 φ ∗ = a 0 ∗ φ 0 + a 1 ∗ φ 1 + a 2 ∗ φ 2 + a 3 ∗ φ 3 \varphi^*=a_0^*\varphi_0+a_1^*\varphi_1+a_2^*\varphi_2+a_3^*\varphi_3 φ∗=a0∗φ0+a1∗φ1+a2∗φ2+a3∗φ3。同样根据公式展开有
( ( φ 0 , φ 0 ) 0 0 0 0 ( φ 1 , φ 1 ) 0 0 0 0 ( φ 2 , φ 2 ) 0 0 0 0 ( φ 3 , φ 3 ) ) \begin{pmatrix} (\varphi_0,\varphi_0) &0&0&0 \\ 0 & (\varphi_1,\varphi_1)&0&0\\ 0&0&(\varphi_2,\varphi_2)&0\\ 0&0&0&(\varphi_3,\varphi_3) \end{pmatrix} ⎝⎜⎜⎛(φ0,φ0)0000(φ1,φ1)0000(φ2,φ2)0000(φ3,φ3)⎠⎟⎟⎞ ( a 0 ∗ a 1 ∗ a 2 ∗ a 3 ∗ ) \begin{pmatrix} a_0^*\\ a_1^*\\ a_2^*\\ a_3^* \end{pmatrix} ⎝⎜⎜⎛a0∗a1∗a2∗a3∗⎠⎟⎟⎞= ( ( φ 0 , f ) ( φ 1 , f ) ( φ 2 , f ) ( φ 3 , f ) ) \begin{pmatrix} (\varphi_0,f)\\ (\varphi_1,f)\\ (\varphi_2,f)\\ (\varphi_3,f) \end{pmatrix} ⎝⎜⎜⎛(φ0,f)(φ1,f)(φ2,f)(φ3,f)⎠⎟⎟⎞
这里就是正交多项式的好处了,除对角线外全为0。 现在,我们再问自己最后一个问题, f f f是什么?我们用 φ ∗ = ∑ a j φ j \varphi^*=\sum a_j\varphi_j φ∗=∑ajφj去逼近 f ( x ) = exp ( x ) f(x)=\exp(x) f(x)=exp(x),因此 f f f就是我们的目标函数 f ( x ) = exp ( x ) f(x)=\exp(x) f(x)=exp(x)。OK,起飞。
离散型
基是 { 1 , x , . . . , x n } \{1,x,...,x^n\} {1,x,...,xn}型(数学模型)
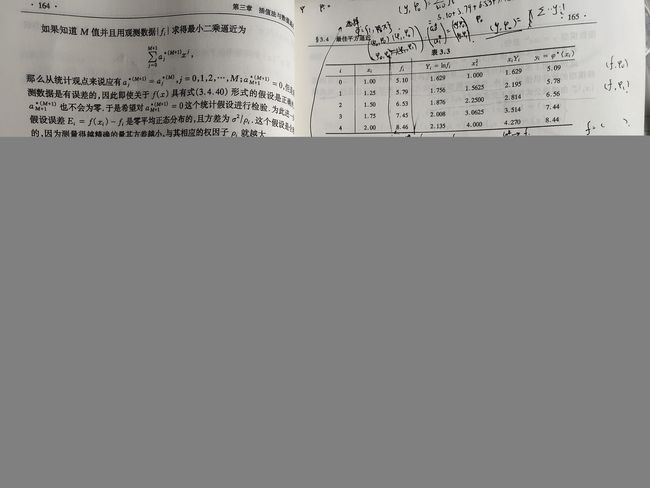
例 : 给 定 数 据 ( x i , f i ) , 试 选 择 适 当 数 学 模 型 , 求 最 小 二 乘 拟 合 函 数 φ ∗ 例:给定数据(x_i,f_i),试选择适当数学模型,求最小二乘拟合函数\varphi^* 例:给定数据(xi,fi),试选择适当数学模型,求最小二乘拟合函数φ∗。
我并不打算讲解这道题,大家可以直接看文末的解析。我想讨论的是题中出现的数学模型。离散型问题完全和连续型问题相似,只是函数内积会发生变化。那么书上为什么在这一章节会出现数学模型这一说法呢?为什么前面的连续型函数没有这个说法呢?为什么对于同一个公式,不同模型给出的结果不同, f i f_i fi不都是相同的嘛? 这一点困惑了我很久,我相信一定有人和我一样。如何理解这个数学模型?好了,那再来一次,为什么我前面一再强调我们需要搞清楚我们的目的,就在理解数学模型时体现出来了。这是我们的公式。

离散情况下的函数内积变化成了如下形式:

题解给出了三种情形。下面请看我分析
-
给定数学模型 y = a ∗ exp ( b x ) y=a*\exp(bx) y=a∗exp(bx),试图以这个数学模型来逼近函数 f f f
我们仍然可以套用之前的做法。假设,我们来到了这一步。

由于基是 { 1 , x , x 2 . . . x n } \{1,x,x^2...x^n\} {1,x,x2...xn},所以我们的 φ 0 = 1 , φ 1 = x \varphi_0=1,\varphi_1=x φ0=1,φ1=x。这里为什么我们只需要两个 φ i \varphi_i φi?原因很简单,因为给出的数学模型中只有两个变量,我们只用求出两个未知数 a 0 ∗ , a 1 ∗ a_0^*,a_1^* a0∗,a1∗。 那么, a 0 ∗ , a 1 ∗ a_0^*,a_1^* a0∗,a1∗是什么呢?我们的目的是什么?我们希望我们有一个函数(或者说数学模型)
用 φ ∗ = a ∗ exp ( b x ) \varphi^*=a*\exp(bx) φ∗=a∗exp(bx)估计题目给出的 f i f_i fi,可是现在 φ ∗ \varphi^* φ∗并不是我们期望的形式 ∑ a j φ j \sum a_j\varphi_j ∑ajφj。所以我们要变形,原式等价于:
用 l n φ ∗ = l n a + b x ln\varphi^*=lna+bx lnφ∗=lna+bx(两边取对数)估计 l n f i lnf_i lnfi。
所以此时,我们的 f f f是 l n f lnf lnf, a 0 ∗ , a 1 ∗ a_0^*,a_1^* a0∗,a1∗分别是 l n a 和 b lna和b lna和b。OK,起飞。 -
给定数学模型 y = 1 a 0 + a 1 x y=\frac{1}{a_0+a_1x} y=a0+a1x1,试图以这个数学模型来逼近函数 f f f
同理,我们继续来阐述我们的目的。
用 φ ∗ = 1 a 0 + a 1 x \varphi^*=\frac{1}{a_0+a_1x} φ∗=a0+a1x1估计题目给出的 f i f_i fi,可是现在 φ ∗ \varphi^* φ∗并不是我们期望的形式 ∑ a j φ j \sum a_j\varphi_j ∑ajφj。所以我们要变形,原式等价于:
用 1 φ ∗ = a 0 + a 1 x ( 倒 数 ) 估 计 1 f i \frac{1}{\varphi^*}=a_0+a_1x(倒数)估计\frac{1}{f_i} φ∗1=a0+a1x(倒数)估计fi1。
所以此时,我们的 f f f是 1 f \frac{1}{f} f1, a 0 ∗ , a 1 ∗ a_0^*,a_1^* a0∗,a1∗分别是 a 0 和 a 1 a_0和a_1 a0和a1。OK,起飞。 -
给定数学模型 y = a 0 + a 1 x + a 2 x 2 y=a_0+a_1x+a_2x^2 y=a0+a1x+a2x2,试图以这个数学模型来逼近函数 f f f
同理,我们继续来阐述我们的目的。
用 φ ∗ = a 0 + a 1 x + a 2 x 2 \varphi^*=a_0+a_1x+a_2x^2 φ∗=a0+a1x+a2x2估计题目给出的 f i f_i fi,现在 φ ∗ \varphi^* φ∗正是我们期望的形式 ∑ a j φ j \sum a_j\varphi_j ∑ajφj。因此,直接我们有
所以此时,我们的 f f f是目标函数 f f f, a 0 ∗ , a 1 ∗ , a 2 ∗ a_0^*,a_1^*,a_2^* a0∗,a1∗,a2∗分别是 a 0 、 a 1 和 a 2 a_0、a_1和a_2 a0、a1和a2。OK,起飞。
看到这里,我想诸位也会明白,事实上,对于所有的逼近,不管是连续还是不连续我们都可以建立基于某个数学模型的最佳平方逼近。 φ ∗ \varphi* φ∗并不是只能为多项式,事实上,因为大多数非多项式函数都能够通过变换变换为多项式函数,因此我们完全能够自己确定我们的 φ ∗ \varphi* φ∗形式,从而去逼近原函数。当然,这一切都是基于文章最开始的公式。
基是任意由 { 1 , x , . . . , x n } \{1,x,...,x^n\} {1,x,...,xn}生成的正交多项式型
例 : 给 定 数 据 ( x i , f i ) , 通 过 正 交 化 方 法 球 二 次 最 佳 平 方 多 项 式 例:给定数据(x_i,f_i),通过正交化方法球二次最佳平方多项式 例:给定数据(xi,fi),通过正交化方法球二次最佳平方多项式。
这道例题我同样不想讲解,大家可以直接看后面的解析。本题的精华在于正交化方法,这也是离散型逼近题型的特点。不像连续型逼近,前辈已经告诉过我们很多正交多项式,我们便不必自己运算,对于离散型我们需要根据给出的 ( x i , f i ) (x_i,f_i) (xi,fi)自己写出正交多项式。具体做法教科书上依然有。这里不详细说明。