CNN网络中的 1 x 1 卷积是什么?
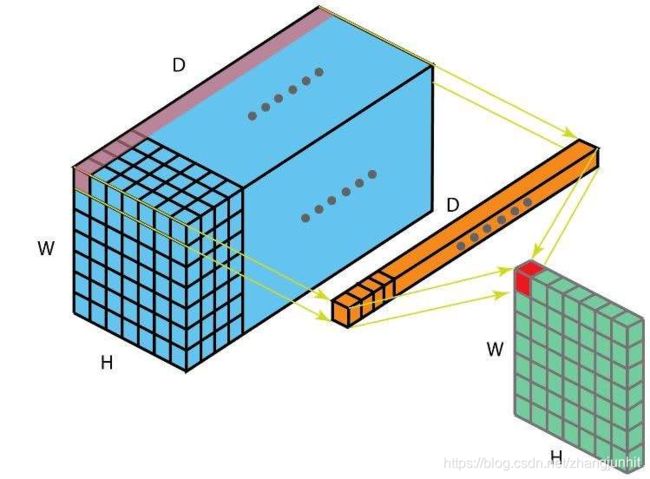
上面是一个 1x1 卷积核的输出示意图, 如果是 K 个1x1 卷积核,那么 结果就是 将通道数由 D 变为 K 降维或升维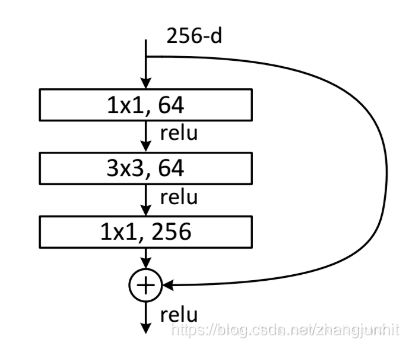
特征通道数变化: 256 —> 64 —> 256
http://cs231n.github.io/convolutional-networks/#convert
这里先来看看全链接层和卷积层联系。
全链接层和卷积层的区别在于卷积层中的神经元只和前一层的局部神经元连接,卷积层中的参数是共享的。全链接层和卷积层中的神经元计算都是点乘,他们的函数形式是一样的。所以全链接层和卷积层是可以相互转换的。
1)对于任意一个卷积层,都有一个全链接层可以实现相同的前向函数功能,权值矩阵将是一个大矩阵,这个矩阵大部分值都是零除了局部块区域(因为是局部连接)其中大部分块的权值是一样的(权值共享)。
2)同样,对于一个全链接层也可以转为卷积层。例如一个全链接层,有4096个神经元,它的输入是 7×7×512,我们可以将这个全链接层表示为下面的卷积层,F=7 filter size,P=0 pad ,S=1 stride ,K=4096 ,the receptive field size of the Conv Layer neurons (F), the stride with which they are applied (S), and the amount of zero padding used § on the border,Number of filters K。换句话说,我们将滤波器的尺寸设置为输入尺寸,这样输出就是 1×1×4096,这样卷积层的输出和全链接层的输出是一样的。
FC->CONV conversion: 在这两种转换中,将全链接层转为卷积层在实际中很有作用。假定一个ConvNet 网络的输入是 224x224x3 图像,经过一系列卷积层和池化层得到 7x7x512的结构,(经过5次池化,224/2/2/2/2/2 = 7)。在 AlexNet 中 使用了 2个4096尺寸的全链接层,最后一个全链接层是1000个神经元,用于输出类别分数。我们将这三个全链接层转为卷积层:
1)将第一个全链接层,其输入是 7x7x512,用一个 filter size F=7 的卷积层代替,得到输出是 1x1x4096
2) 将第二个全链接层 用一个 filter size F=1 的卷积层代替, 输出是 1x1x4096
3) 将最后一个全链接层用一个 filter size F=1 的卷积层代替,输出是 1x1x1000
上面的转换在实际中主要是通过操作权值矩阵 W 来实现的。这种转换对于计算更大的图像中很多空间位置的响应很高效,可以在大图像上滑动整个 ConvNet 网络,在单次前向计算中。
例如,如果 224x224的图像得到 7x7x512,经过32倍的降维,那么对于 384x384 图像 对应的得到 12x12x512, 384/32=12。 接着上面的三个卷积层(从全链接层转化的)处理,我们得到最后的结果是 6x6x1000,注意这里不是1x1x1000,而是对应 384x384 整个图像的结果 6x6。
这里我们得到 6x6 =36个位置的结果 比计算 36次 效率要搞很多,因为 这个 7x7x512 结果是可以为后面三个卷积所共享的。
1x1 convolution. As an aside, several papers use 1x1 convolutions, as first investigated by Network in Network. Some people are at first confused to see 1x1 convolutions especially when they come from signal processing background. Normally signals are 2-dimensional so 1x1 convolutions do not make sense (it’s just pointwise scaling). However, in ConvNets this is not the case because one must remember that we operate over 3-dimensional volumes, and that the filters always extend through the full depth of the input volume. For example, if the input is [32x32x3] then doing 1x1 convolutions would effectively be doing 3-dimensional dot products (since the input depth is 3 channels).
1x1 卷积 如果只对2维信号处理,那么它只是一个比例缩放,但是 ConvNets 处理的是三维信息,例如输入是 32x32x3 ,对其进行 1x1 卷积,那么将进行 3 维的点乘,因为 输入深度是 3个通道。
According to the NIN paper, 1x1 convolution is equivalent to cross-channel parametric pooling layer。
From the paper - “This cascaded cross channel parameteric pooling structure allows complex and learnable interactions of cross channel information”.
http://iamaaditya.github.io/2016/03/one-by-one-convolution/
Simple Answer
Most simplistic explanation would be that 1x1 convolution leads to dimension reductionality. For example, an image of 200 x 200 with 50 features on convolution with 20 filters of 1x1 would result in size of 200 x 200 x 20. But then again, is this is the best way to do dimensionality reduction in the convoluational neural network? What about the efficacy vs efficiency?
对于 1x1 卷积简单的解释是 降低维度信息。例如对于一个 图像,有 50个 大小为 200 x 200 的特征图,使用 20个filters 1x1的卷积,得到 200 x 200 x 20 输出。但是这种降维在卷积网络中是最优的吗? 有效性如何?
Complex Answer
Feature transformation
Although 1x1 convolution is a ‘feature pooling’ technique, there is more to it than just sum pooling of features across various channels/feature-maps of a given layer. 1x1 convolution acts like coordinate-dependent transformation in the filter space[1]. It is important to note here that this transformation is strictly linear, but in most of application of 1x1 convolution, it is succeeded by a non-linear activation layer like ReLU. This transformation is learned through the (stochastic) gradient descent. But an important distinction is that it suffers with less over-fitting due to smaller kernel size (1x1).
1x1 卷积 尽管是一种 ‘特征池化’技术,它不仅仅是对给定网络层的跨通道/特征图池化。1x1 卷积 是依赖于坐标位置的映射变换,在滤波空间里的。这种映射本来是严格线性的,但是在CNN网络中 大部分 1x1 卷积 后面会加上非线性激活响应 如 ReLU。这个映射是通过梯度下降算法学习的。这种 1x1 卷积 因为 kernel size 很小,所以不容易过拟合。