leetcode 组合总和

一，题目描述：

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

• 所有数字（包括 target）都是正整数。
• 解集不能包含重复的组合。 

示例 1:

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
  [7],
  [2,2,3]
]

示例 2:

输入: candidates = [2,3,5], target = 8,
所求解集为:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

二，解题思路：

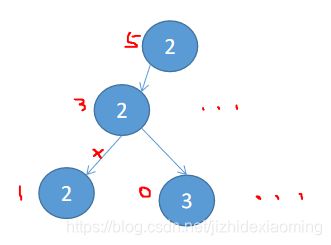
先由小到大排序，然后利用回溯法。关键如何写好递归函数，递归函数传递的变量：备选数组，目标值，开始选择的位置，当前路径，所有路径。示例[2,3,6,7]，target=7：

1）开始选择2, 则target变成7-2=5, 这样就变成了找数组和为5的组合，当前路径是（2）；

2）因为5>2，即目标值是大于备选数组中的一些值的，所以可以继续选，从第一个开始选2, target 变成5-2=3，当前路径是（2,2）；

3）继续target 变成3-2=1, 当前路径变成（2,2,2）；

4）因为target = 1是小于备选数组内最小的值2, 即a>1, 所以2+2+2+a>7 , 所以被选数组中其他任何值都不可能满足; 退一步，变成当前路径是(2,2)，当前target=3; 开始的备选位置往后移一个，变成从备选数组3开始选；

5）选择3，则target变成3-3=0，则刚好符合，当前路径为（2,2,3），找到一个；

6）退一格，看看其他路径是否也行，当前路径变成（2,2），开始的备选位置往后移一个，变成从备选数组4开始选；

。。。形成的选择树如下：

三，C++代码：

class Solution {
public:
    vector> combinationSum(vector& candidates, int target) {
        vector> res;
        vector cur;
        sort(candidates.begin(), candidates.end());
        dfs(candidates, target, 0, cur, res);
        
        return res;
    }
    void dfs(vector& candidates, int target, int start, vector& cur, vector>& res){
        if (target == 0){
            res.push_back(cur);
            return;
        }
        for (int i = start; i < candidates.size(); i++){
            if (target < candidates[i]) // 比如target值是7，备选数组的最小值是9，那肯定找不到
                return;
            cur.push_back(candidates[i]); // 否则，candidates[i]的这条路可以走
            dfs(candidates, target - candidates[i], i, cur, res);
            cur.pop_back(); // 当前的路径不通，退一步，或者此路刚好可以，退一步试试其他路是否可以
        }
    }
};