硬核分享：游戏中迷人天空的颜色是如何制作出来的？

转载请注明文章来源于腾讯游戏学院

文丨spaceoddity42腾讯互动娱乐 工程师

几个世纪以来，天空一直是许多艺术家迷恋的主题，他们试图尽可能准确地描绘其颜色。同样的，在游戏开发中，天空渲染对于游戏开发者也一直是一个迷人的主题，本文理论部分译自scratchapixel，介绍了天空渲染的理论基础，并在此基础上了建立相应的数学模型，最后在ShaderToy上通过Pixel Shader来实现相应的算法。

本章我们将学习大气散射，推荐先阅读体积渲染和次表面散射的内容（详见www.scratchapixel.com），它们和本主题包含类似的概念，大气散射可以看作是体积渲染的扩展。

1、大气散射的理论基础

1.1 介绍

几个世纪以来，天空一直是许多艺术家迷恋的主题，他们试图尽可能准确地描绘其颜色。在19世纪到20世纪之前，许多物理学家和数学家痴迷于弄清楚是什么导致天空在日落和日出时呈现橙色，白天呈现蓝色。从历史上看，大气散射的发现归功于瑞利（又名John Strutt，获得诺贝尔奖的英国物理学家），其主要工作是在19世纪产生的（瑞利接替了剑桥大学的麦克斯韦，后者因其在电磁方面的贡献而闻名，计算机图形很大一部分的研究与麦克斯韦的工作有关，瑞利还和普朗克研究了黑体）。大气散射也会对物体的外观产生影响，这种效应被称为空气透视（绘画中多称为大气透视），被莱昂纳多达芬奇首次观察、研究和应用在他的画作中（事实上，这种技术可以在达芬奇作品之前的绘画作品中找到）。随着物体和观察者之间的距离增加，物体的颜色被大气的颜色所取代（对于天空来说，它通常在白天呈现蓝色，日出和日落时呈现红橙色）。这是一个重要的视觉线索，因为人们通过比较它们相对于彼此有多蓝来判断场景中物体的距离。在（数字）绘画中，空气透视可以极大地帮助增加图像的深度（大脑可以更容易地处理比另一个更远的物体），如下为达芬奇画作复制品（注意后面的岩石的颜色受到大气的影响）。

在计算机图形学史上，Nishita在1993年发表了一篇开创性的论文”Display of the Earth Taking into account Atmospheric Scattering”，他在这篇论文中描述了一种模拟天空颜色的算法，有趣的是他的这篇论文和他在1996年写的关于同一主题的另一篇论文"Display Method of the Sky Color Taking into Account Multiple Scattering"不完全是关于大气模拟，更多是关于从外太空看到的地球的真实渲染（包括渲染海洋表面、云层和大陆）。

Figure 1:Top, a real photograph of the Earth from outer space. Bottom, a simulation using Nishita's model. These images have been copied from the paper "Display of the Earth taking into account Atmospheric Scattering" written by Nishita in 1993 (c) Siggraph.

这提醒了我们在这些年里，计算机图形技术的发展是由制造业推动的，用于精确模拟其产品或提供3D虚拟训练环境，而不是娱乐行业（电影和游戏）。Nishita描述的模拟天空的技术从他的时代以来没有太大变化，在该领域的大部分研究都集中在GPU上实现Nishita的算法，而模拟质量没有任何明显改善（更多关注的是速度和实时仿真）。在1999年发表于Siggraph的一篇论文”A Practical Analytic Model for Daylight”中，Preetham等人描述了另一种天空模型，正如其标题所示，这是一个分析模型，它提供了对天空颜色的精确模拟，但它比Nishita提出的技术有更多限制（例如，该模型仅适用于位于地面上的观察者）。值得一提的是Jensen等人在2011年Siggraph上发表的一篇模拟夜空的论文”A Physically-Based Nightsky Model”，本章将给出Nishita模型的实现。

在后面小节中，我们将描述各种现象，它们组合在一起呈现天空的颜色，然后我们将展示Nishita的算法如何模拟这些现象，一旦我们在程序中实现了该模型，我们可以轻松扩展该技术以模拟空气透视，通过改变模型的参数，我们还可以创建外星天空。

1.2 大气模型

大气层是行星周围的一层气体，由于行星的引力，大气层保持在适当的位置，大气层的主要关注点是它的厚度和成分（组成大气层的不同成分）。地球大气层厚度约为100km（由卡门线划定，卡门线是公认的外太空与地球大气层的分界线），它由氧气、氮气、氩气（瑞利发现的气体）、二氧化碳和水蒸气组成。然而，在模拟中，我们将使用60km的厚度（我们只考虑在地球大气的前两层，对流层和平流层中的散射）。如果你阅读有关体积渲染的内容（建议首先看这部分内容再来看本篇内容），你将知道光子在与粒子碰撞时会散射。当光在某个方向上穿过一个体积（大气）时，光子在与粒子碰撞时会往其他方向上偏转，这种现象称为散射。光被粒子散射的频率取决于粒子的性质（主要是它们的大小）和它们的密度（单位体积中有多少粒子/分子）。我们现在已经知道了地球大气层的分子大小，我们也知道它们的浓度/密度。我们将使用这些科学测量数据来进行大气散射模拟。地球周围大气层的另一个重要方面是这些颗粒的密度随高度的增加而减小。换句话说，比如在海平面上每单位立方体空气中的分子比海洋上方2公里多。这是一个重要的事实，因为散射量取决于我们刚刚提到的分子密度。当光在大气层中从上层传播到地面时，我们需要沿着光线按固定间隔对大气密度进行采样，并根据这些样本位置处的大气密度计算散射量（我们将使用数值积分，下一步会详细解释）。大多数论文（包括Nishita的论文）都假设大气密度随高度呈指数下降。换句话说，它可以用以下形式的简单方程建模：

其中density(0)是海平面的空气密度，h是我们测量大气密度时的高度（海拔高度），H是大气密度均匀时的大气厚度（在科学论文中，H被称为大气标高，大气密度每经过一段距离H其值就减少为原来的值的1/e，H取决于温度）。一些论文声称这个模型是一个很好的近似，但是其他一些人声称它不准确，并且更喜欢将天空密度模拟为一系列同心层，每个同心层由它们的厚度和密度决定。（论文出处未知）

将天空密度建模为一系列层（在Nishita的论文中称为球壳）从计算的角度来看具有优势。由于我们将沿着光线朝着观察者的路径执行数值积分，在密度高的大气中采集的样本比在密度低的情况下采集的样本更重要，因此沿着光线执行“固定步长”积分将导致收敛性差。如今计算机速度如此之快以至于我们可以通过固定步长来强制执行此计算，但在Nishita那个时候，优化算法是必要的。因此，Nishita提出了一个模型，其中大气层用一系列球形壳体表示，在低海拔使用较小间隔，在高海拔使用较长间隔。但请注意，在论文中发表的图表中，层的厚度似乎非常像按指数形式变化的，这并不令人惊讶，因为每个壳的半径在Nishita的模型中由空气分子的密度分布精确确定。

大气层由小颗粒（空气分子）组成，小颗粒也会在低空与较大的颗粒混合，称为气溶胶。这些颗粒可以是由风扬起的灰尘或沙子，也可以是因为空气污染而存在的任何颗粒。它们肯定会对大气的外观产生影响，特别是因为它们不像空气分子那样散射光线。空气分子对光的散射称为瑞利散射，气溶胶对光的散射称为米氏散射。

Figure 2: aerosols present in the atmosphere are responsible for haze.

简而言之，瑞利散射（空气分子散射光）是造成天空蓝色（以及日出和日落时的红橙色）的原因，而米氏散射（气溶胶散射光）通常是造成污染城市上方白灰色雾霾的原因（阴霾掩盖了天空的清晰度，见图2）。如果没有提到使用者需要指定行星和天空的半径，模型将是不完整的，这些数字将用于计算沿观察者和光线方向上样本位置的高度。对于地球，我们将使用Re = 6360 km（e代表地球）和Ra = 6420 km（a代表大气层）。该模型中与距离相关的所有距离和参数应在同一单位系统中表示（km、m等）。

Figure 3: a simple graphical representation of the atmospheric model we will be using in this lesson. It is defined by the radius of the planet (Re) and the radius of the atmosphere (Ra). The atmosphere is made of aerosols (mainly present at low altitude) and air molecules. Density of particles decreases exponentially with altitude. This diagram is not to scale.

对于大气模型，这可能是棘手的，因为行星的大小可能很大。对于这样的尺寸，公里通常是更合适的选择。然而，散射系数非常小，并且它们更容易用米或毫米（对于光波长甚至用纳米）来表示。选择一个好的单位也是因为浮点数精度的限制（也就是说，如果数字太大或太小，计算机对这些数字的浮点表示可能会变得不准确，从而导致计算错误）。模型的输入参数可以用不同的单位表示，并由程序内部转换。

最后，我们通过指定天空的主要照明来源是太阳这一点来完成我们对模型的描述，太阳离地球太远，我们可以假设所有到达大气层的光线都是相互平行的，我们将进一步展示这种假设如何简化模型的实现。

Figure 4: the sun is so far away from the Earth, that each light ray reaching the Earth's atmosphere can be considered as being parallel to each other.

1.3 瑞利散射

瑞利在19世纪晚期发现了空气分子对光的散射。他特别指出，这种现象具有强烈的波长依赖性，更准确地说，空气分子散射的蓝光比绿光和红光更多（ps：更容易散射蓝光）。这种形式的散射和他提出的计算由分子（例如我们在大气中找到的分子）组成的体积的散射系数的方程，仅适用于尺寸远小于构成可见光的波长的颗粒（粒子应至少比散射波长小十分之一）。可见光的波长在380到780 nm之间变化，440,550和680分别被认为是蓝色，绿色和红色光的波长峰值，我们将在本文的其余部分使用这些值。瑞利散射方程提供了计算已知分子密度的体积的散射系数。在关于大气散射的文献中，散射系数由希腊字母β（beta）表示。

上标S用于标识散射，下标R用于标识瑞利（用于将这些系数与米氏散射系数区分开）。在这个等式中，h是高度，λ是波长，N是海平面的分子密度，n是空气的折射率，是大气标高。在我们的模拟中，我们将使用=8km（如果需要，请参见网上的大气标高以获得更精确的测量数据）。正如你所看到的，具有短波长的光（例如蓝光）的β值比长波长的光（红色）更高，这解释了白天天空呈现蓝色的原因。当来自太阳的光穿过大气层时，相比绿色和红色光，蓝色光更多地向观察者散射。为什么在日出和日落时会出现红橙色？在此种情况下（日出、日落时），相比于太阳高于头部（天顶位置）时,来自太阳的光必须在大气层中行进更长部分以到达观察者的位置。那距离相当长，大部分蓝光在到达观察者的位置之前已经散开，而一些不像蓝光一样散射的红光仍然存在。因此，日出和日落时的天空呈现红橙色（有时可以是紫色或略带绿色）。我们可以使用一个N，n的测量值来计算β，但是我们将使用在海平面的散射系数的预计算值（波长440、550和680nm，对应的散射系数分别是：、、，注意蓝光的散射系数大于绿光和红光的散射系数）。通过应用方程的指数部分（右项），我们可以调整任何给定高度h的这些系数。

Nishita的论文和我们在本篇中提到的其他论文的主要问题之一是他们要么没有给出N，n等的值来生成论文中显示的图像。在使用测量数据时，论文的作者通常不会引用它们的来源。在海平面上寻找分子密度的科学数据并不容易，如果你有任何关于此主题的有用链接或信息，你可以向我们提供，我们希望收到你的来信。我们在本篇中使用的海平面散射系数可以在两篇论文中找到："Efficient Rendering of Atmospheric Phenomena", by Riley et al. and "Precomputed Atmospheric Scattering" by Bruneton et al.

我们不会详细介绍空气密度，但可以在互联网上找到有关此问题的有趣信息。在本篇中，我们真正需要的是海平面的平均散射系数，它们可以很好地重建天空的颜色，但是学习如何计算这些系数将会让任何想要更好地控制大气模型的好奇读者感兴趣。

如果你阅读有关体积渲染的内容，你将会知道用于渲染参与介质的物理模型是散射系数，吸收系数和相函数，它描述光在与粒子碰撞时散射的程度和方向。到目前为止，在本篇中，我们只给出了地球大气层的散射系数值（并解释了如何计算）。对于大气散射，通常认为吸收系数可忽略不计，换句话说，我们将假设大气不吸收光。还记得在体积渲染的内容中，我们在渲染参与介质时使用的物理模型中需要的衰减系数是吸收系数和散射系数的总和，因此（因为吸收系数为零）衰减系数可以表示为：

瑞利相函数看起来像这样：

其中μ是光与视线方向之间角度的余弦（见图8）。

1.4 米氏散射

米氏散射在某种程度上类似于瑞利散射，但适用于尺寸大于散射波长的粒子（比如我们在地球大气层的低海拔地区发现的气溶胶）。如果我们将瑞利方程应用于气溶胶，不会得到令人信服的图像。渲染散射系数的米氏方程如下所示：

下标M标识米氏散射，注意，对于米氏散射存在特定的大气标高，其通常设定为1.2km。与瑞利散射相反，我们不需要方程来计算米氏散射系数。我们将使用海平面测量值来代替。对于米氏散射，我们将使用：。气溶胶的密度也随着海拔高度呈指数下降，同瑞利散射类似，我们将通过在方程（由大气标高调制）的右边包含一个指数项来模拟这种效应。米氏相函数方程是：

米氏相函数包括控制介质各向异性的项g（瑞利相函数不包括），气溶胶具有很强的前向指向性，一些论文使用g=0.76（我们也将使用这个值作为我们的默认值）。

1.5 光学深度的概念

在实现算法之前，我们将把所有零散部分放在一起。首先，我们应该注意到，天空只不过是围绕实心球体的球形体积。因为它只是一个体积，为了渲染天空，我们可以使用光线步进算法，这是最常用的渲染参与介质的技术。我们在关于体积渲染的课程中详细研究了该算法。当我们渲染一个体积时，观察者（或相机）可以在体积内部或外部。

当相机在体积内时，我们需要找到观察光线离开体积的点，当它在体积外时，我们需要找到观察光线进入和离开体积的点。因为天空是一个球体，我们将使用光线与球体相交测试的方式来计算这些点。我们通过使用地面作为参考来测试相机位于大气层内部或外部。如果此高度大于大气厚度，则摄像机位于大气层之外，并且观察光线可能在两个地方与大气层相交。

Figure 6: the camera can either be inside the atmosphere or outside. When it is inside, we are only interested in the intersection point between the camera ray and the atmosphere. When the camera is outside it can intersect the atmosphere in two points.

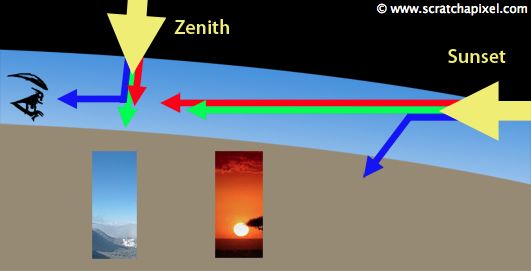
现在我们假设摄像机在地面上（或高出地面一米），但该算法适用于任意摄像机位置。让我们假设我们有一个观察光线（对应于帧中的一个像素），我们知道这条光线与大气层上边缘相交的位置。我们此时需要解决的问题是找出有多少光线在沿着观察者的方向上传播。正如我们在下图中看到的那样，我们的相机或观察者不太可能直视太阳（那样会伤害你的眼睛）。

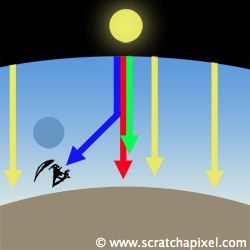Figure 7: single scattering is responsible for the sky color. A viewer is rarely directly looking at the sun (which is dangerous). However when we are looking away from the sun the atmosphere has a color which is the result of blue lightfrom the sunlight being scattered in the direction of the observer's eyes.

如果你朝天空的方向看，你不应该看到任何东西，因为你正在看空旷的空间（天体之间的空间）。然而，事实是你会看到蓝色，这是由来自太阳的光进入大气并被观察方向上的空气分子偏转引起的。换句话说，沿着观察方向没有来自太阳的直射光（除非观察方向直接指向太阳），但是来自太阳的光被大气散射，一些光线最终沿着你的眼睛方向行进。这种现象称为单次散射（在体积渲染内容中对此进行了解释）。

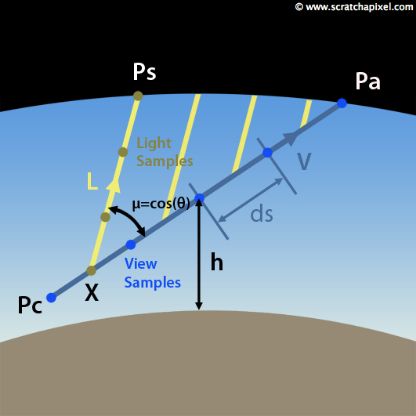Figure 8: to compute the sky color we first trace a ray from Pc to Pa and then integrate the amount of light coming from the sun (with direction L) that is reflected back along that ray (V).

到目前为止我们知道什么？我们知道，为了渲染帧中一个像素对应的天空颜色，我们将首先从点Pc（相机位置）向感兴趣的方向上投射观察光线（V）。我们将计算此光线与大气相交的点Pa。最后，我们需要计算由于单次散射而沿着该光线传播的光量。该值可以使用我们在体积渲染内容中研究的体积渲染方程来计算：

其中T是点Pc和X（沿观察方向的样本位置）之间的透射率。L是体积中位置X处的光量。它所说的是，在Pc到达观察者的光总量等于沿着观察方向V散射的所有太阳光。该量可以通过将沿V的各个位置（X）的光相加来获得，这种技术称为数值积分。我们沿着光线采集的样本越多，结果越好，但计算所需的时间越长。等式中的透射率项（T）解释了在每个样本位置（X）处沿观察者方向V散射的光从X行进到Pc时也会衰减。

回想一下体积渲染的内容，当光线从体积中的一个点移动到另一个点时因吸收和散射，光线会衰减。我们称Pb点的光量为Lb，从Pb到达Pa点的光量为La。存在参与介质的情况下，La（从Pb接收的光）将低于Lb。透射率表示La与Lb之比，因此T在0到1的范围内。透射率的方程看起来像这样：

简单来说，这个等式意味着我们需要测量沿着路径光线Pa-Pb在不同样本位置处的大气的衰减βe，将这些值加起来，将它们乘以长度段ds（即距离Pa-Pb除以使用的样本数量） ，取该值的负值并将其提供给指数函数。

Figure 9: as light (Lb) travels from Pb to Pa, it gets attenuated because of out-scattering and absorption. The result is La. Transmittance is the amount of light received at Pa from Pb, after it was attenuated while traveling through the atmosphere (that is T=La/Lb).

回到我们所说的关于瑞利散射的内容，你会记得βs（我们将以此计算βe）可以用海平面上的散射系数来计算，该散射系数由高度h与大气标高（H）比值的指数函数来计算。

对于瑞利散射，可以忽略吸收，散射系数我们可以写作：

你可以将βe（0）移出积分（因为它是常数），透射率方程重新写为：

指数函数内的和可以看作Pa和Pb之间的平均密度值，并且方程本身在文献中通常称为点Pa-Pb之间的大气的光学深度。

1.6 将阳光加起来

最后，我们将使用前一段中介绍的渲染方程来计算天空颜色，让我们再写一遍：

我们已经解释了如何计算透射率，现在让我们看看Lsun（X）这个量，并解释如何评估它的值。Lsun（X）对应于在样本位置X处沿观察方向散射的太阳光量。为了评估它，首先我们需要计算到达X的光量，直接取阳光强度是不够的，实际上，如果光线在Ps点进入大气层，它也会在行进到X过程中衰减。因此，我们需要使用与我们用于计算沿着从Pa到Pc的观察方向传播的光的衰减的方程相似的方程来计算这种衰减（等式1）：

Equation 1

从技术上讲，对于沿着观察射线的每个采样位置X，我们将需要在太阳光方向（L）上投射光线并找到该光线与大气相交的位置（Ps）。然后，我们将使用与观察射线相同的数值积分技术来评估等式1中的透射率（或光学深度）项。将光线切割成段，并评估每个光段中心的大气密度。构建计算天空颜色的算法的最后一个要素是根据光线方向本身和视线方向来计算在观察方向上散射的光量。这是相函数的作用，瑞利散射和米氏散射有各自的相函数，我们在之前提到过它们。如果你需要了解相函数，请阅读体积渲染相关内容。简而言之，相函数是描述来自方向L的光在方向V上散射多少的函数。米氏相函数包含一个额外项g，称为平均余弦（可能还有其他名称），它定义光是否主要沿前向（L）或后向（-L）散射。对于前向散射，g在[0：1]范围内，而后向散射g在[-1：0]范围内。当g等于零时，光在所有方向上均匀散射，我们说散射是各向同性的。对于米氏散射，我们将g设置为0.76。

最后，我们需要考虑这样的事实，例如，瑞利散射的蓝光主要沿着视线方向散射。为了反映这一点，我们将前一个方程的结果乘以散射系数（βs），这给出了方程的光量部分的完整方程。但是回想一下βs随高度而变化（它的值是高度的函数），其中h是X相对于地面的高度（更精确地说是海平面）：

对于地球大气而言，太阳是天空中唯一的光源，但是，为了写出前一个方程的通用形式，我们应该考虑光可能来自多个方向的事实。在科研论文中，你通常会看到这个等式被写为4π的积分，它描述了传入方向的范围。这个更通用的方程也可以考虑了地面反射的阳光（多次散射），我们将在本章中忽略这些多次散射的阳光。

1.7 计算天空颜色

把所有的元素拼接在一起我们得到以下方程（方程2和方程3）：

Equation 2

Equation 3

将方程3代入方程2得到以下方程：

相函数的结果以及阳光强度是恒定的，我们可以将这两项移到积分外：

Equation 4

这是用于渲染特定视角和光照方向的天空颜色的最终方程。因此，它并不复杂，但对它的计算要求更高，因为我们计算积分并对指数函数进行多次调用（通过透射率项）。另外，你需要记住它们的天空颜色实际上是瑞利和米氏散射的结果。因此，对于每种散射类型，我们需要计算两次这个方程：

在微积分中，两个底数相同的指数函数的乘积可用法则计算，即底数不变指数相加。

我们可以利用这个属性（我们计算一个指数而不是两个）并重新编写方程4中两个透射项的乘法：

Equation 5

2、大气散射的GPU编码实现

在第一部分中已经介绍了相应的理论基础，在这部分我们将在GPU中实现对天空颜色的模拟。由于原文中给出的代码是在CPU中实现的，输出最终的图片需要一定时间且不方便调试预览，因此我们利用ShaderToy在GPU中实现，方便修改参数并实时预览最终模拟的效果，最终效果如下视频所示，可以看到随着太阳接近地平线，靠近地平线位置的天空呈现红色和橙色，另外也可在ShaderToy中看到该实现

（https://www.shadertoy.com/view/3sSfDz）：

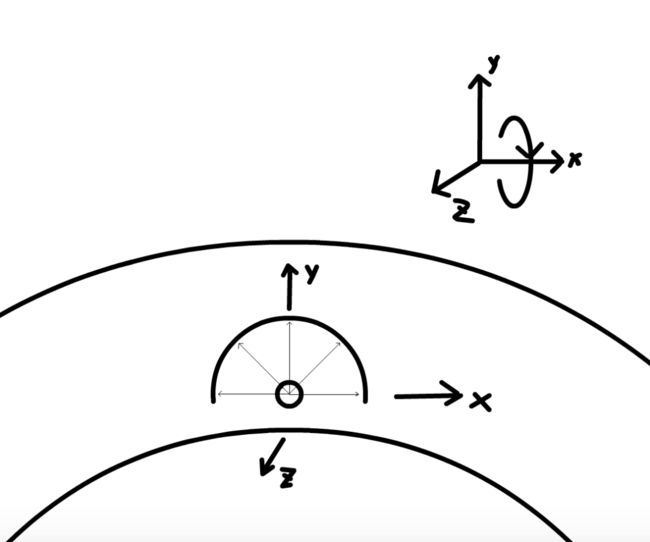
Figure 9

下面开始介绍实现部分，首先是坐标系的建立，想象一下中午你东西向躺在草坪上，太阳在天空正上方，你戴着墨镜直视太阳，以视线直视方向为y轴正方向，双臂展开从左手到右手的方向为x轴正方向，从你的脚底到头顶的方向为z轴正方向，坐标轴的原点在地心，以此建立一个左手坐标系。在此坐标系下平躺着朝着正上方用鱼眼相机每隔一定时间拍摄一次照片，至太阳落山为止，最终将图像序列按创建时间顺序压缩成视频，便得到和如上视频中类似的效果。为了模拟鱼眼效果，需要将单位正方形内的点集映射到单位半球面（不是严格的半球面，有一部分点在半球面以下，关于平面点集到半球面点集的映射，可参考《Ray Tracing from the Ground Up》中有关内容）上，然后从相机位置处向半球面上的这些点发射射线计算每个点上最终的颜色值。

在ShaderToy中，屏幕从左到右为x正向，从下到上为y正向，uv的x和y分量取值范围为「0，1」，但屏幕的长宽不同，屏幕长度大于宽度，这意味着同一把尺子分别与x和y轴平行时投影得到的度量不同，x值会更大些，为了消除这种不一致，需要将uv值的y分量乘以屏幕的长宽比，然后利用球面坐标系的角度和坐标的转换公式得到单位正方形内的点对应的单位半球面上的点，viewScale是为了对面画整体进行缩放，类似于FOV的作用。

vec2uv=(2.*fragCoord/iResolution.xy1.)*vec2(iResolution.x/iResolution.y,1.);

floatviewScale=1.;

vec2p=uv*viewScale;

注意屏幕的xy平面相当于上面建立的坐标系的xz平面，因此我们可以做如下映射：

//单位正方形内的点映射到半球面上

floatz2=p.x*p.x+p.y*p.y;

floatphi=atan(p.y,p.x);

floattheta=acos(1.-z2);

vec3dir=vec3(sin(theta)*cos(phi),

cos(theta),

sin(theta)*sin(phi));

ray r=ray(vec3(0.,earthRadius+1.,0.),dir);

color=getIncidentLight(r);

fragColor=vec4(color,1.);

我们将相机位置放置在(0.,earthRadius+1.0,0.)处，将屏幕坐标中单位正方形内的点映射到新建立的坐标系中单位半球面上的点，然后从相机位置处向半球面上各个已映射的点发射射线。由于模拟的是正午到日落的动态效果，需要更新太阳的位置，假设太阳从正午到日落沿着我们建立的坐标轴的x轴旋转了90度，则可以对太阳光的方向做如下更新：

//sun position

floatrotSpeedFactor=3.;

mat3sunRot=rotate_around_x(-abs(sin(u_time/rotSpeedFactor))*90.);

sunDir*=sunRot;

沿x轴旋转的变换矩阵可由如下辅助函数得到：

//绕x轴的旋转矩阵

mat3rotate_around_x(constinfloatdegrees)

{

floatangle=radians(degrees);

float_sin=sin(angle);

float_cos=cos(angle);

returnmat3(1.,0.,0.,

0.,_cos,-_sin,

0.,_sin,_cos);

}

接着我们定义一些宏和常量：

#definePI3.14159265359

#defineUSE_HENYEY1

#defineu_res iResolution

#defineu_time iTime

vec3sunDir=vec3(0.,1.,0.);

floatsunPower=20.;

constfloatearthRadius=6360e3;

constfloatatmosphereRadius=6420e3;

constintnumSamples=16;

constintnumSamplesLight=8;//光线与大气层顶端交点到采样点的采样数量

constfloathR=7994.;//rayleigh

constfloathM=1200.;//mie

constvec3betaR=vec3(5.5e-6,13.0e-6,22.4e-6);//rayleigh

constvec3betaM=vec3(21e-6);//mie

然后定义射线和球的struct以及射线与球相交检测以及计算相交点的辅助函数：

structray

{

vec3origin;

vec3direction;

};

structsphere

{

vec3center;

floatradius;

};

//表示大气层的球

constsphere atmosphere=sphere(vec3(0.,0.,0.),atmosphereRadius);

//计算射线与球是否相交以及交点

boolraySphereIntersect(constinray r,constinsphere s,inoutfloatt0,inoutfloatt1)

{

vec3oc=r.origin-s.center;

floata=dot(r.direction,r.direction);

floatb=dot(oc,r.direction);

floatc=dot(oc,oc)-s.radius*s.radius;

floatdiscriminant=b*b-(a*c);

if(discriminant>0.0)

{

floattmp=sqrt(discriminant);

t0=-b-tmp;

t1=-b+tmp;

returntrue;

}

returnfalse;

}

另外瑞利和米氏以及schlick相函数的定义如下：

//----------------phase function----------------

floatrayleighPhaseFunc(floatmu)

{return3.*(1.+mu*mu)/(16.*PI);

}

constfloatg=0.76;

floathenyeyGreensteinPhaseFunc(floatmu)

{

return(1.-g*g)/((4.*PI)*pow(1.+g*g-2.*g*mu,1.5));

}

constfloatk=1.55*g-0.55*(g*g*g);

floatschlickPhaseFunc(floatmu)

{

return(1.-k*k)/(4.*PI*(1.+k*mu)*(1.+k*mu));

}

//----------------phase function----------------

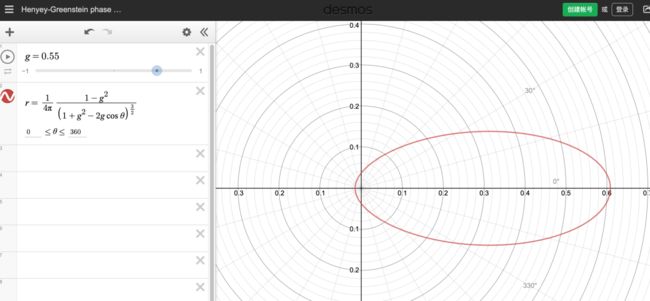
相函数定义为粒子在各个方向上的实际散射能，与粒子散射为各向同性时该方向的散射能之比，输出是一个无量纲的值。可以通过desmos上的henyeyGreensteinPhaseFunction的图像来配合理解。

由于理论中提到最终的颜色值是由积分公式计算得到的，积分区间是一个连续的区间，因此只能通过离散采样的方式计算累加和得到近似结果。

//计算光学深度

boolgetSunLight(constinray r,inoutfloatopticalDepthR,inoutfloatopticalDepthM)

{

floatt0,t1;

raySphereIntersect(r,atmosphere,t0,t1);

floatmarchPos=0.;

floatmarchStep=t1/float(numSamplesLIght);

for(inti=0;i<numSamplesLIght;i++)

{

//相邻两个采样点的中点

vec3s=r.origin+r.direction*(marchPos+0.5*marchStep);

floatheight=length(s)-earthRadius;

if(height<0.)

returnfalse;

opticalDepthR+=exp(-height/hR)*marchStep;

opticalDepthM+=exp(-height/hM)*marchStep;

marchPos+=marchStep;

}

returntrue;

}

vec3getIncidentLight(constinray r)

{

floatt0,t1;

if(!raySphereIntersect(r,atmosphere,t0,t1))

{

returnvec3(0.);

}

floatmarchStep=t1/float(numSamples);

floatmu=dot(r.direction,sunDir);

floatphaseR=rayleighPhaseFunc(mu);

floatphaseM=

#ifUSE_HENYEY

henyeyGreensteinPhaseFunc(mu);

#else

schlickPhaseFunc(mu);

#endif

floatopticalDepthR=0.;

floatopticalDepthM=0.;

vec3sumR=vec3(0.);

vec3sumM=vec3(0.);

floatmarchPos=0.;

for(inti=0;i<numSamples;i++)

{

vec3s=r.origin+r.direction*(marchPos+0.5*marchStep);

floatheight=length(s)-earthRadius;

//计算光学深度累加和

floathr=exp(-height/hR)*marchStep;

floathm=exp(-height/hM)*marchStep;

opticalDepthR+=hr;

opticalDepthM+=hm;

ray lightRay=ray(s,sunDir);

floatopticalDepthLightR=0.;

floatopticalDepthLightM=0.;

boolbOverGround=getSunLight(lightRay,opticalDepthLightR,opticalDepthLightM);

if(bOverGround)

{

vec3t=betaR*(opticalDepthR+opticalDepthLightR)+

betaM*1.1*(opticalDepthM+opticalDepthLightM);

vec3attenuation=exp(-t);

sumR+=hr*attenuation;

sumM+=hm*attenuation;

}

marchPos+=marchStep;

}

returnsunPower*(sumR*phaseR*betaR+sumM*phaseM*betaM);

}

通过调整瑞利散射系数或米氏散射系数，可以得到一些alien planet atmosphere的效果，如下所示：

此外，如果从相机位置处向成像平面发射射线计算着色，可得到如下渲染效果，比较接近unity中默认场景的天空颜色：

大气渲染相关的技术点很多，本文仅实现了单次散射，对于多次散射、相函数推导、优化等相关主题未有涉及，在实时渲染中还有其他简化模型以及各种trick来渲染天空。

• 投稿邮箱：[email protected]

• 商务合作：Amber（微信：lcxk6876767）

• 其他合作：老林（微信：sea_bug）