牛客网 剑指offer:
https://www.nowcoder.com/ta/coding-interviews
1.二维数组中的查找
左到右递增,上到下递增;
解法:从左下遍历。大于则x--,小于则y++。
public class Solution { public boolean Find(int target, int [][] array) { int m = array.length; int n = array[0].length; int x = m - 1; int y = 0; while (x >= 0 && y <= n - 1) { if (array[x][y] > target) x--; else if (array[x][y] < target) y++; else return true; } return false; } }
2.替换空格
直接遍历:
public class Solution { public String replaceSpace(StringBuffer str) { String rst = ""; for (int i = 0; i < str.length(); i++) { if (str.charAt(i) == ' ') rst += "%20"; else rst += str.charAt(i); } return rst; } }
要求原字符串上修改:
从前往后替换,后面字符要不断移动,效率低;从后往前,只需要移动一次,效率高。
两个指针一次从newLen和Len从后向前移动;
public class Solution { public String replaceSpace(StringBuffer str) { int spaceNum = 0; for (int i = 0; i < str.length(); i++) { if (str.charAt(i) == ' ') spaceNum++; } int newLen = str.length() + spaceNum * 2; int i = str.length() - 1; int j = newLen - 1; str.setLength(newLen); for (; i >= 0; i--) { if (str.charAt(i) == ' ') { str.setCharAt(j--,'0'); str.setCharAt(j--,'2'); str.setCharAt(j--,'%'); } else { str.setCharAt(j--,str.charAt(i)); } } return str.toString(); } }
3.从尾到头打印链表
利用ArrayList特性,头插法;据说时间复杂度高?
import java.util.ArrayList; public class Solution { public ArrayListprintListFromTailToHead(ListNode listNode) { ArrayList list = new ArrayList (); while (listNode != null) { list.add(0,listNode.val); listNode = listNode.next; } return list; } }
递归
import java.util.ArrayList; public class Solution { ArrayListlist = new ArrayList (); public ArrayList printListFromTailToHead(ListNode listNode) { if (listNode != null) { this.printListFromTailToHead(listNode.next); list.add(listNode.val); } return list; } }
栈
(注意:如果用for循环stack.size要赋值保存,不然每次pop后size会变化就出错了)
存节点:
import java.util.Stack; import java.util.ArrayList; public class Solution { public ArrayListprintListFromTailToHead(ListNode listNode) { ArrayList list = new ArrayList (); Stack stack = new Stack (); while (listNode != null) { stack.push(listNode); listNode = listNode.next; } while (!stack.empty()) { list.add(stack.pop().val); } return list; } }
存数值:
import java.util.Stack; import java.util.ArrayList; public class Solution { public ArrayListprintListFromTailToHead(ListNode listNode) { ArrayList list = new ArrayList (); Stack stack = new Stack (); while (listNode != null) { stack.push(listNode.val); listNode = listNode.next; } while (!stack.empty()) { list.add(stack.pop()); } return list; } }
4.重建二叉树
根据前序和中序重建二叉树;递归;preStart, inStart, inEnd;
5.用两个栈实现队列
实现push和pop操作;
栈A用来作入队列;
栈B用来出队列,当栈B为空时,栈A全部出栈到栈B,栈B再出栈(即出队列);
import java.util.Stack; public class Solution { Stackstack1 = new Stack (); Stack stack2 = new Stack (); public void push(int node) { stack1.push(node); } public int pop() { if (stack2.empty()){ while (!stack1.empty()) { stack2.push(stack1.pop()); } } return stack2.pop(); } }
6.旋转数组的最小数字
[5,6,7,1,2,3,4] 左边递增右边递减;
1.首先判断lo和hi,如果lo
public class Solution { public int findMin(int[] nums) { int lo = 0, hi = nums.length - 1; while (lo < hi) { if (nums[lo] < nums[hi]) return nums[lo]; int mid = lo + (hi - lo) / 2; if (nums[mid] >= nums[lo]) lo = mid + 1; else hi = mid; } return nums[lo]; } }
7.斐波那契数列
迭代
public class Solution { public int Fibonacci(int n) { if (n == 0) return 0; int a = 1; int b = 1; for (int i = 1; i < n; i++) { int tmp = a + b; a = b; b = tmp; } return a; } }
8.跳台阶
递归
public class Solution { public int JumpFloor(int n) { if (n == 1) return 1; if (n == 2) return 2; return JumpFloor(n - 1) + JumpFloor(n - 2); } }
迭代(就是斐波那契)
public class Solution { public int JumpFloor(int n) { int a = 1; int b = 2; for (int i = 1; i < n; i++) { int tmp = a + b; a = b; b = tmp; } return a; } }
9.变态跳台阶
f(n)=f(n-1)+f(n-2)+...+f(1)
f(n)=2*f(n-1);
public class Solution { public int JumpFloorII(int n) { int[] a = new int[n]; a[0] = 1; int sum = 1; for (int i = 1; i < n; i++) { a[i] = sum + 1; sum += a[i]; } return a[n - 1]; } }
public class Solution { public int JumpFloorII(int n) { return 1 << --n; } }
10.矩形覆盖
public class Solution { public int RectCover(int n) { if (n == 0 || n == 1 || n == 2) return n; return RectCover(n - 1) + RectCover(n - 2); } }
11.二进制中1的个数
位运算;n&(n-1) 把最右的1置零;
public class Solution { public int NumberOf1(int n) { int cnt = 0; while (n != 0) { n = n & (n - 1); cnt++; } return cnt; } }
12.数值的整数次方
举例:10^1101 = 10^0001*10^0100*10^1000。
public class Solution { public double Power(double base, int n) { double res = 1; int e; if (n == 0) return 1; else if (n < 0) e = -n; else e = n; while(e!=0){ if( (e & 1) ==1 ) res *= base; base *= base;// 翻倍 e >>= 1;// 右移一位 } return n >= 0 ? res : (1 / res); } }
13.调整数组顺序使奇数位于偶数前面
(1,2,4,3,6,5,7) -> (1,3,5,7, 2,4,6)
要求相对位置不变,所以不能用双指针了。申请一个新数组保存偶数;
public class Solution { public void reOrderArray(int [] array) { int[] tmp = new int[array.length]; int m = 0; int n = 0; for (int i = 0; i < array.length; i++) { if (array[i] % 2 != 0) array[m++] = array[i]; //奇数放到对应位置; else tmp[n++] = array[i]; //偶数放在tmp数组保存; } for (int i = 0; i < n; i++) { array[m++] = tmp[i]; } } }
用插入排序思想的话时间复杂度是O(n^2);
14.链表中倒数第k个结点
双指针,滑动窗口;测试用例要考虑下k>length的情况;
public class Solution { public ListNode FindKthToTail(ListNode head,int k) { if (head == null || k <= 0) return null; ListNode dummy = new ListNode(0); dummy.next = head; head = dummy; ListNode right = head; for (int i = 0; i < k; i++) { right = right.next; if (right == null) return null; } while (right.next != null) { right = right.next; head = head.next; } return head.next; } }
15.反转链表
(四步:1.tmp保存下一节点; 2.head指向prev; 3.head移动; 4.prev移动)
public class Solution { public ListNode ReverseList(ListNode head) { ListNode pre = null; while (head != null) { ListNode tmp = head.next; head.next = pre; pre = head; head = tmp; } return pre; } }
16.合并两个排序的链表
递归:
public ListNode Merge(ListNode list1,ListNode list2) { if(list1 == null){ return list2; } if(list2 == null){ return list1; } if(list1.val <= list2.val){ list1.next = Merge(list1.next, list2); return list1; }else{ list2.next = Merge(list1, list2.next); return list2; } }
非递归:三个指针head、list1、list2;注意第一个节点的处理,dummy固定,head移动;
public class Solution { public ListNode Merge(ListNode list1,ListNode list2) { ListNode dummy = new ListNode(0); ListNode head = dummy; while (list1 != null && list2 != null) { if (list1.val <= list2.val) { head.next = list1; list1 = list1.next; } else { head.next = list2; list2 = list2.next; } head = head.next; } if (list1 != null) head.next = list1; if (list2 != null) head.next = list2; return dummy.next; } }
17.树的子结构
ps:这题和之前做过的题不一样。。之前要求子树到叶子完全重合才是subtree,但是本题只要是属于的关系就是true;
例如{8,8,7,9,2,#,#,#,#,4,7},{8,9,2};在原题就是false的,但本题是true。。
todo
18.二叉树的镜像
递归;栈;
import java.util.Stack; public class Solution { public void Mirror(TreeNode root) { /*递归解法; if (root == null) return; Mirror(root.right); Mirror(root.left); TreeNode tmp = root.right; root.right = root.left; root.left = tmp; */ /*非递归解法*/ if (root == null) return; Stackstack = new Stack (); stack.push(root); while (!stack.empty()) { TreeNode cur = stack.pop(); if (cur.left != null) stack.push(cur.left); if (cur.right != null) stack.push(cur.right); TreeNode tmp = cur.right; cur.right = cur.left; cur.left = tmp; } } }
19.顺时针打印矩阵
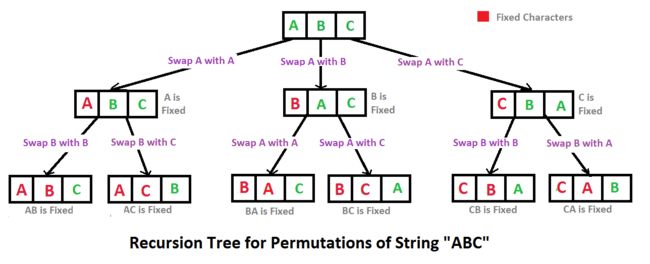
螺旋矩阵;用cnt做每轮螺旋的“外壁”,while(cnt*2 20.包含min函数的栈 使用两个栈stack和minStack,对于push操作,需要和minStack的peek()比较大小;(注:stack和minStack大小始终相同) 21.栈的压入、弹出序列: (辅助栈;每次辅助栈入栈,比较辅助栈peek和pop栈当前指针j的值,相同则pop辅助栈,j指针移动;最后判断辅助栈stack是否为空) (注:while循环内必须加判断stack.empty) 【思路】借用一个辅助的栈,遍历压栈顺序,先将第一个放入栈中,这里是1,然后判断栈顶元素是不是出栈顺序的第一个元素,这里是4,很显然1≠4,所以我们继续压栈,直到相等以后开始出栈,出栈一个元素,则将出栈顺序向后移动一位,直到不相等,这样循环等压栈顺序遍历完成,如果辅助栈还不为空,说明弹出序列不是该栈的弹出顺序。 举例: 入栈1,2,3,4,5 出栈4,5,3,2,1 首先1入辅助栈,此时栈顶1≠4,继续入栈2;此时栈顶2≠4,继续入栈3;此时栈顶3≠4,继续入栈4; 此时栈顶4=4,出栈4,弹出序列向后一位,此时为5,辅助栈里面是1,2,3 此时栈顶3≠5,继续入栈5 此时栈顶5=5,出栈5,弹出序列向后一位,此时为3,,辅助栈里面是1,2,3 …. 22.层序遍历 队列Queue;size,for循环添加左右; 23.二叉搜索树的后序遍历序列 递归,后序遍历序列满足去掉最后一个root,剩下两部分前一部分小于root,后一部分大于root; (helper(a[], start, end) 首先index遍历到第一个不大于[end]的位置,然后从start开始遍历到index判断是否大于[end],大于则false;递归) BST的后序序列的合法序列是,对于一个序列S,最后一个元素是x (也就是根),如果去掉最后一个元素的序列为T,那么T满足:T可以分成两段,前一段(左子树)小于x,后一段(右子树)大于x,且这两段(子树)都是合法的后序序列。完美的递归定义 : ) 。 24.二叉树和为某一值的路径 回溯法;helper(root, tar, A 终止条件:root==null; 叶子节点:=tar则, list-add, rst-add, remove, return; 递归过程:add(), helper()左右递归,remove; 25.复杂链表的复制 26.二叉搜索树与双向链表 27.字符串的排列 按字典序返回字符串字符的所有排列; 例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。 回溯法 helper(char[] cs, int i, ArrayList list): 如果i是最后一位,则找到一个解,不包含则添加; 如果i不是最后一位,for循环i,swap+递归+复位swap; 主函数:helper、Collections.sort(rst)排序; 28.数组中出现次数超过一半的数字 使用count计数;为0则赋值,相同cnt+,不同cnt-; 由于主数字不一定存在,所以需要再遍历一次验证; 29.topK最小的k个数 30.连续子数组的最大和 动态规划(维护两个变量:maxEndingHere和maxSoFar;) 解法:(从A[0]开始向右遍历,如果已经解决了A[0]-A[i-1]中的最大连续subarray,那么A[0]-A[i]的最大连续subarray要么是A[0]-A[i-1]的结果,要么是以A[i]作为结尾的一段subarray;记前者是maxSoFar,后者是maxEndingHere;显然maxEndingHere的值为(前一个数的maxEndingHere加上A[i])或者(A[i])这两个数之间的最大值。) 31.1到n中1出现的次数 todo 32.把数组排成最小的数 先将整型数组转换成String数组,然后将String数组排序,最后将排好序的字符串数组拼接出来。 实现比较器:Arrays.sort(str, new Comparator 关键就是制定排序规则。 * 排序规则如下: 33.丑数 求第n个丑数(只含2.3.5因子): (new ArrayList, uglys.add(1),定义3个指针p2/p3/p5,分别代表指向3个数组中已添加的位置;和uglys的LastNumber比较,<=则指针后移一位;取3个数组所指的min作为uglys.add;注意get(p)指向的是已经添加到uglys中的数;所以代码中用到的都需要是get(p)*2/3/5) (ArrayList 1-n的丑数:1,2,3,4,5,6,8,9,10,12,15…… 可以分为如下3组: (1)1, 1×2, 2×2, 3×2, 4×2, 5×2, 6×2, 8×2, … 只需每次添加的数为3组中最小的值 34.第一个只出现一次的字符 解法1:HashMap统计次数 + 再次遍历; 解法2:大小为('z'-'A'+1)的数组 注ASCII值:A-Z 为 65-90; a-z 为 97- 122; 35.数组中的逆序对 解法:(归并排序。mergeSort, merge; 分成若干小数组,求出逆序对个数,再归并得出总个数。注意[left]>[right]时,sum+=mid-left+1 因为right的小数已经放入tmp数组里不参与left后面的比较了,而left后的数都大于left) 牛客的要取余: 36.两个链表的第一个公共结 解法1:HashSet; 解法2:(把两个链表相接;则环的起始位置即是结果--即ListCycleII问题。题目要求链表结构不变,最后还需要把index的null节点置null) 解法3:遍历两个长度,长的先移动; 37.数字在有序数组中出现次数 有序数组,二分求范围; 38.二叉树的深度 递归: 迭代,层序遍历思想: 39.平衡二叉树 三个条件:深度差<=1 + 左右子树为平衡二叉树; 递归 + depth函数; 40.两个只出现一次的数字 其他都出现了两次; 解法1:HashSet 解法2:位运算、异或 当只有一个数出现一次时,我们把数组中所有的数,依次异或运算,最后剩下的就是落单的数,因为成对儿出现的都抵消了。 FindFirst1(bitRst):找第一个bit结果为1的位置index; isBit1(tar, index):判断index位置的bit是否为1; 41.和为S的连续正数序列 双指针,lo和hi,初始化为前两个;小于sum则hi++,大于sum则lo++;lo增加到(1+sum)/2时停止; 42.和为S的两个数字 数组递增;如果有多对,输出乘积最小的; 解法1:HashSet; 因为可能不存在,所以设置了一个boolean变量标记状态; 解法2:双指针; 和相同,那么相差最大的乘积最小; 左右双指针,>sum则hi--, 43.左旋转字符串 三次reverse翻转;由于string不支持修改字符,所以要先转char数组; 如果允许使用subString方法: 44.翻转单词顺序列 str.trim(); str.split(" "); 45.扑克牌顺子 46..圆圈中最后剩下的数 47.求1到n的和 要求不能使用乘除法、for、if等关键字; 48. 不用加减乘除做加法 A+B:(x=x^y, y=(x&y)<<1) 位运算实现整数加法本质就是用二进制进行运算。其主要用了两个基本表达式: x^y //执行加法,不考虑进位。 我们来做个3位数的加法: 49.字符串转换成整数 参考一下lintcode版本的吧; 解法:(1.判空/null; 2.判断正负符号;3.遍历str,把数字添加到rst,rst=rst*10+(charAt(i)-0); 4.添加符号; 5.考虑溢出,转int) 50.数组中第一个重复的数字 长度为n的数组,数字在0到n-1范围内;输出第一个重复过的数字 解法1:辅助数组或者hashset 优化一下,用boolean数组,boolean只占一位 解法2:不用额外空间,不过会改变数组元素; 题目里写了数组里数字的范围保证在0 ~ n-1 之间,所以可以利用现有数组设置标志,当一个数字被访问过后,可以设置对应位上的数 + n,之后再遇到相同的数时,会发现对应位上的数已经大于等于n了,那么直接返回这个数即可。 51.构建乘积数组 B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。 52.正则表达式匹配 53.表示数值的字符串 54.字符流中第一个不重复 数组;一个字符占8位,因此不会超过256个,可以申请一个256大小的数组实现一个简易哈希表。 55.链表中环的入口结点 先slow和fast移动,再head和slow.next比较和移动; (1-2-3-[4-5-6-7-8-9-10], 如果slow和fast都从1开始move, 当相遇时, slow移动了k步, fast移动了2k步(绕换n圈,则2k-k=nr), 相遇地点距离循环首结点距离为m; 只要head节点从首结点开始移动, 移动k-m步, slow从meet点移动,移动k-m步; 这时候两者就在cycle首结点相遇。因为slow已经移动了k步,再移动k步就是又到了meet点,所以移动k-m步就是到cycle的首结点) ps:此解法要求slow.next=head;因为fast多移动了一步; 56.删除链表中重复的结点 删除所有重复结点;三个一组(h->h.n->h.n.n) 比较h.n和h.n.n的val,一旦发现有重复值,则保存重复值,内循环while删除掉所有的对应结点; 57.二叉树的下一个结点 中序遍历的下一个结点 58.对称的二叉树 递归: (左节点和右节点的比较,所以需要helper函数,判断left和right的null与val;递归左左和右右,左右和右左) 迭代: (Stack, 每次pop两个对称的节点,判断两个节点是否满足条件。再push进四个节点) 59.Z型层序遍历 设置flag,分list.add()和list.add(0,val)两种情况; 1.Queue;2.while:size、list; 3.for():poll、list、queue; 4.flag,rst; 60.层序遍历 61.序列化二叉树 62.二叉搜索树的第K大结点 中序遍历,使用计数器; 递归: 63.数据流中的中位数 一个大根堆,一个小根堆; todo 64.滑动窗口的最大值 双端队列; todo ![]()
![]()
import java.util.ArrayList;
public class Solution {
public ArrayList
![]()
![]()
import java.util.Stack;
public class Solution {
Stack
![]()
![]()
import java.util.ArrayList;
import java.util.Stack;
public class Solution {
public boolean IsPopOrder(int [] pushA,int [] popA) {
if (pushA.length != popA.length) return false;
if (pushA == null) return true;
Stack
![]()
![]()
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public ArrayList
![]()
![]()
/**
* T: 二叉搜索树的后序遍历序列
*
* 题目描述
* 输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。
* 如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
*
*
*/
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
int n = sequence.length;
if (n == 0) return false;
if (n == 1) return true;
return helper(sequence, 0, n - 1);
}
public boolean helper(int[] a, int start, int end) {
if (start >= end) return true;
int index = end - 1;
while (index >= start && a[index] > a[end]) {
index--;
}
for (int i = start; i < index; i++) {
if (a[i] > a[end]) return false;
}
return helper(a, start, index) && helper(a, index + 1, end - 1);
}
}
![]()
![]()
import java.util.ArrayList;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public ArrayList
![]()
![]()
/*
public class RandomListNode {
int label;
RandomListNode next = null;
RandomListNode random = null;
RandomListNode(int label) {
this.label = label;
}
}
*/
public class Solution {
public RandomListNode Clone(RandomListNode pHead){
if (pHead == null) return null;
//复制
RandomListNode pCur = pHead;
while (pCur != null) {
RandomListNode node = new RandomListNode(pCur.label);
node.next = pCur.next;
pCur.next = node; //添加复制节点node;
pCur = node.next; //移动pCur;
}
//random节点
pCur = pHead;
while (pCur != null) {
if (pCur.random != null) pCur.next.random = pCur.random.next;
pCur = pCur.next.next;
}
//拆分
RandomListNode newHead = pHead.next;
RandomListNode newCur = newHead;
pCur = pHead;
while (pCur != null) {
pCur.next = newCur.next;
if(newCur.next != null)newCur.next = newCur.next.next;
pCur = pCur.next;
newCur = newCur.next;
}
return newHead;
}
}
![]()
![]()
//直接用中序遍历
public class Solution {
TreeNode head = null;
TreeNode realHead = null;
public TreeNode Convert(TreeNode pRootOfTree) {
ConvertSub(pRootOfTree);
return realHead;
}
private void ConvertSub(TreeNode pRootOfTree) {
if(pRootOfTree==null) return;
ConvertSub(pRootOfTree.left);
if (head == null) {
head = pRootOfTree;
realHead = pRootOfTree;
} else {
head.right = pRootOfTree;
pRootOfTree.left = head;
head = pRootOfTree;
}
ConvertSub(pRootOfTree.right);
}
}
![]()
![]()
链接:https://www.nowcoder.com/questionTerminal/947f6eb80d944a84850b0538bf0ec3a5
来源:牛客网
解题思路:
1.将左子树构造成双链表,并返回链表头节点。
2.定位至左子树双链表最后一个节点。
3.如果左子树链表不为空的话,将当前root追加到左子树链表。
4.将右子树构造成双链表,并返回链表头节点。
5.如果右子树链表不为空的话,将该链表追加到root节点之后。
6.根据左子树链表是否为空确定返回的节点。
public TreeNode Convert(TreeNode root) {
if(root==null)
return null;
if(root.left==null&&root.right==null)
return root;
// 1.将左子树构造成双链表,并返回链表头节点
TreeNode left = Convert(root.left);
TreeNode p = left;
// 2.定位至左子树双链表最后一个节点
while(p!=null&&p.right!=null){
p = p.right;
}
// 3.如果左子树链表不为空的话,将当前root追加到左子树链表
if(left!=null){
p.right = root;
root.left = p;
}
// 4.将右子树构造成双链表,并返回链表头节点
TreeNode right = Convert(root.right);
// 5.如果右子树链表不为空的话,将该链表追加到root节点之后
if(right!=null){
right.left = root;
root.right = right;
}
return left!=null?left:root;
}
![]()
![]()
import java.util.*;
public class Solution {
public ArrayList Permutation(String str) {
ArrayList res = new ArrayList();
if (str != null && str.length() > 0) {
helper(str.toCharArray(), 0, res);
Collections.sort(res);
}
return res;
}
public void helper(char[] cs, int i, ArrayList list) {
if(i == cs.length - 1) {
String val = String.valueOf(cs);
if (!list.contains(val))
list.add(val);
} else {
for(int j = i; j < cs.length; ++j) {
swap(cs, i, j);
helper(cs, i + 1, list);
swap(cs, i, j);
}
}
}
public void swap(char[] str, int i, int j) {
if (i != j) {
char t = str[i];
str[i] = str[j];
str[j] = t;
}
}
}
![]()
![]()
public class Solution {
public int MoreThanHalfNum_Solution(int [] array) {
int count = 1;
int len = array.length;
int rst = array[0];
for (int i = 1; i < len; i++) {
if (count == 0) {
rst = array[i];
}
if (rst == array[i]) count++;
else count--;
}
//验证;
count = 0;
for (int i = 0; i < len; i++) {
if (array[i] == rst) count++;
}
if (count * 2 > len) return rst;
return 0;
}
}
基于堆排序算法,构建最大堆。时间复杂度为O(nlogk)
![]()
![]()
import java.util.ArrayList;
public class Solution {
public ArrayList
![]()
![]()
public static int maxSubArray(int[] A) {
int maxSoFar=A[0], maxEndingHere=A[0];
for (int i=1;i
![]()
![]()
链接:https://www.nowcoder.com/questionTerminal/bd7f978302044eee894445e244c7eee6
来源:牛客网
class Solution {
public:
int NumberOf1Between1AndN_Solution(int n)
{
//主要思路:设定整数点(如1、10、100等等)作为位置点i(对应n的各位、十位、百位等等),分别对每个数位上有多少包含1的点进行分析
//根据设定的整数位置,对n进行分割,分为两部分,高位n/i,低位n%i
//当i表示百位,且百位对应的数>=2,如n=31456,i=100,则a=314,b=56,此时百位为1的次数有a/10+1=32(最高两位0~31),每一次都包含100个连续的点,即共有(a%10+1)*100个点的百位为1
//当i表示百位,且百位对应的数为1,如n=31156,i=100,则a=311,b=56,此时百位对应的就是1,则共有a%10(最高两位0-30)次是包含100个连续点,当最高两位为31(即a=311),本次只对应局部点00~56,共b+1次,所有点加起来共有(a%10*100)+(b+1),这些点百位对应为1
//当i表示百位,且百位对应的数为0,如n=31056,i=100,则a=310,b=56,此时百位为1的次数有a/10=31(最高两位0~30)
//综合以上三种情况,当百位对应0或>=2时,有(a+8)/10次包含所有100个点,还有当百位为1(a%10==1),需要增加局部点b+1
//之所以补8,是因为当百位为0,则a/10==(a+8)/10,当百位>=2,补8会产生进位位,效果等同于(a/10+1)
int count=0;
long long i=1;
for(i=1;i<=n;i*=10)
{
//i表示当前分析的是哪一个数位
int a = n/i,b = n%i;
count=count+(a+8)/10*i+(a%10==1)*(b+1);
}
return count;
}
};
* 若ab > ba 则 a > b,
* 若ab < ba 则 a < b,
* 若ab = ba 则 a = b;
* 解释说明:
* 比如 "3" < "31"但是 "331" > "313",所以要将二者拼接起来进行比较![]()
![]()
import java.util.*;
public class Solution {
public String PrintMinNumber(int [] numbers) {
if(numbers == null || numbers.length == 0) return "";
int len = numbers.length;
String[] str = new String[len];
StringBuilder sb = new StringBuilder();
for(int i = 0; i < len; i++){
str[i] = String.valueOf(numbers[i]);
}
Arrays.sort(str,new Comparator
(2)1, 1×3, 2×3, 3×3, 4×3, 5×3, 6×3, 8×3, …
(3)1, 1×5, 2×5, 3×5, 4×5, 5×5, 6×5, 8×5, … ![]()
![]()
import java.util.ArrayList;
public class Solution {
public int GetUglyNumber_Solution(int n) {
ArrayList
![]()
![]()
import java.util.HashMap;
public class Solution {
public int FirstNotRepeatingChar(String str) {
HashMap
![]()
![]()
public class Solution {
public int FirstNotRepeatingChar(String str) {
int[] a = new int['z' - 'A' + 1];
for (int i = 0; i < str.length(); i++){
a[str.charAt(i) - 'A']++;
}
for (int i = 0; i < str.length(); i++) {
if (a[str.charAt(i) - 'A'] == 1) return i;
}
return -1;
}
}
![]()
![]()
public class Solution {
/**
* @param A an array
* @return total of reverse pairs
*/
public long reversePairs(int[] A) {
// Write your code here
return mergeSort(A, 0, A.length - 1);
}
public int mergeSort(int[] A, int low, int high) {
if (low >= high) return 0;
int mid = (low + high) / 2;
int sum = 0;
sum += mergeSort(A, low, mid);
sum += mergeSort(A, mid + 1, high);
sum += merge(A, low, mid, high);
return sum;
}
public int merge(int[]A, int low, int mid, int high) {
int[] tmp = new int[high - low + 1];
int left = low;
int right = mid + 1;
int k = 0;
int sum = 0;
while (left <= mid && right <= high) {
if (A[left] <= A[right]) {
tmp[k++] = A[left++];
} else {
tmp[k++] = A[right++];
sum += mid - left + 1;
}
}
while (left <= mid) {
tmp[k++] = A[left++];
}
while (right <= high) {
tmp[k++] = A[right++];
}
for (int i = 0; i < tmp.length; i++) {
A[i + low] = tmp[i];
}
return sum;
}
}
![]()
![]()
public class Solution {
public int InversePairs(int [] A) {
return mergeSort(A, 0, A.length - 1) ;
}
public int mergeSort(int[] A, int low, int high) {
if (low >= high) return 0;
int mid = (low + high) / 2;
int sum = 0;
sum += mergeSort(A, low, mid) ;
sum += mergeSort(A, mid + 1, high);
sum += merge(A, low, mid, high);
return sum % 1000000007;
}
public int merge(int[]A, int low, int mid, int high) {
int[] tmp = new int[high - low + 1];
int left = low;
int right = mid + 1;
int k = 0;
int sum = 0;
while (left <= mid && right <= high) {
if (A[left] <= A[right]) {
tmp[k++] = A[left++];
} else {
tmp[k++] = A[right++];
sum = (sum + (mid - left + 1)) % 1000000007 ;
}
}
while (left <= mid) {
tmp[k++] = A[left++];
}
while (right <= high) {
tmp[k++] = A[right++];
}
for (int i = 0; i < tmp.length; i++) {
A[i + low] = tmp[i];
}
return sum;
}
}
![]()
![]()
public class Solution {
/**
* @param headA: the first list
* @param headB: the second list
* @return: a ListNode
*/
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// Write your code here
if (headA == null || headB == null) return null;
ListNode index = headA;
while (index.next != null) index = index.next;
index.next = headB;
ListNode rst = listCycle(headA);
index.next = null;
return rst;
}
public ListNode listCycle(ListNode head) {
ListNode slow = head, fast = head.next;
if (fast == null || fast.next == null) return null;
while (slow != fast) {
slow = slow.next;
fast = fast.next.next;
}
slow = head;
fast = fast.next;
while (slow != fast) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
![]()
![]()
public class Solution {
public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
ListNode cur1 = pHead1;
ListNode cur2 = pHead2;
int len1 = 0;
int len2 = 0;
while (cur1 != null) {
cur1 = cur1.next;
len1++;
}
while (cur2 != null) {
cur2 = cur2.next;
len2++;
}
cur1 = pHead1;
cur2 = pHead2;
if (len2 > len1) {
for (int i = 0; i < len2 - len1; i++) {
cur2 = cur2.next;
}
} else if (len1 > len2) {
for (int i = 0; i < len1 - len2; i++) {
cur1 = cur1.next;
}
}
while (cur1 != null) {
if (cur1 == cur2) return cur1;
cur1 = cur1.next;
cur2 = cur2.next;
}
return cur1;
}
}
![]()
![]()
public class Solution {
public int GetNumberOfK(int [] a , int tar) {
if (a == null || a.length == 0) return 0;
//FindFirstPos;
int lo = 0;
int hi = a.length - 1;
while (lo < hi) {
int mid = (lo + hi) / 2;
if (a[mid] < tar) lo = mid + 1;
else hi = mid;
}
if (a[lo] != tar) return 0;
int firstPos = lo;
//FindLastPos;
hi = a.length - 1;
while (lo < hi) {
int mid = (lo + hi + 1) / 2;
if (a[mid] > tar) hi = mid - 1;
else lo = mid;
}
int cnt = hi - firstPos + 1;
return cnt;
}
}
![]()
![]()
public class Solution {
public int TreeDepth(TreeNode root) {
if (root == null) return 0;
return Math.max(TreeDepth(root.left), TreeDepth(root.right)) + 1;
}
}
![]()
![]()
public class Solution {
public int maxDepth(TreeNode root) {
//Iterative--层序遍历思想
if (root == null) return 0;
Queue
![]()
![]()
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
if (root == null) return true;
return Math.abs(depth(root.left) - depth(root.right)) <= 1 && IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right);
}
public int depth(TreeNode root) {
if (root == null) return 0;
return Math.max(depth(root.left), depth(root.right)) + 1;
}
}
![]()
![]()
public class Solution {
public boolean isBalanced(TreeNode root) {
return height(root) != -1;
}
public int height(TreeNode root) {
if (root == null) return 0;
int lh = height(root.left);
if (lh == -1) return -1;
int rh = height(root.right);
if (rh == -1) return -1;
if (Math.abs(lh - rh) > 1) return -1;
return Math.max(lh, rh) + 1;
}
}
![]()
![]()
import java.util.*;
//num1,num2分别为长度为1的数组。传出参数
//将num1[0],num2[0]设置为返回结果
public class Solution {
public void FindNumsAppearOnce(int [] a,int num1[] , int num2[]) {
HashSet
![]()
![]()
public class Solution {
public void FindNumsAppearOnce(int[] array, int[] num1, int[] num2) {
int length = array.length;
if(length == 2){
num1[0] = array[0];
num2[0] = array[1];
return;
}
int bitResult = 0;
for(int i = 0; i < length; ++i){
bitResult ^= array[i];
}
int index = findFirst1(bitResult);
for(int i = 0; i < length; ++i){
if(isBit1(array[i], index)){
num1[0] ^= array[i];
}else{
num2[0] ^= array[i];
}
}
}
private int findFirst1(int bitResult){
int index = 0;
while(((bitResult & 1) == 0) && index < 32){
bitResult >>= 1;
index++;
}
return index;
}
private boolean isBit1(int target, int index){
return ((target >> index) & 1) == 1;
}
}
![]()
![]()
import java.util.ArrayList;
/*
*初始化small=1,big=2;
*small到big序列和小于sum,big++;大于sum,small++;
*当small增加到(1+sum)/2是停止
*/
public class Solution {
public ArrayList
![]()
![]()
import java.util.*;
public class Solution {
public ArrayList
![]()
![]()
import java.util.ArrayList;
public class Solution {
public ArrayList
![]()
![]()
public class Solution {
public String LeftRotateString(String str,int n) {
char[] chars = str.toCharArray();
if(chars.length < n) return "";
reverse(chars, 0, n-1);
reverse(chars, n, chars.length-1);
reverse(chars, 0, chars.length-1);
return new String(chars);
}
public void reverse(char[] chars,int low,int high){
char temp;
while(low<high){
temp = chars[low];
chars[low] = chars[high];
chars[high] = temp;
low++;
high--;
}
}
}
![]()
![]()
public class Solution {
public String LeftRotateString(String str,int n) {
//保证旋转的位数大于字符串的长度,否则返回空字符串
if (str == null || str.length() == 0) return str;
n = n % str.length();
String s1 = str.substring(0, n);
String s2 = str.substring(n,str.length());
return s2 + s1;
}
}
![]()
![]()
public class Solution {
public String ReverseSentence(String str) {
if(str.trim().equals("")){
return str;
}
String[] a = str.split(" ");
StringBuffer o = new StringBuffer();
int i;
for (i = a.length; i >0;i--){
o.append(a[i-1]);
if(i > 1){
o.append(" ");
}
}
return o.toString();
}
}
思路:利用逻辑与的短路特性实现递归终止。(前面假则后面不执行) 当n==0时,(n>0)&&((sum+=Sum_Solution(n-1))>0)只执行前面的判断,为false,然后直接返回0;当n>0时,执行sum+=Sum_Solution(n-1),实现递归计算Sum_Solution(n)。![]()
![]()
class Solution {
public int Sum_Solution(int n) {
int sum = n;
boolean ans = (n>0)&&((sum+=Sum_Solution(n-1))>0);
return sum;
}
}
(x&y)<<1 //进位操作
令x=x^y ;y=(x&y)<<1 进行迭代,每迭代一次进位操作右面就多一位0,最多需要“加数二进制位长度”次迭代就没有进位了,此时x^y的值就是结果。
101+011=1000 //正常加法
位运算加法:
(1) 101 ^ 011 = 110
(101 & 011)<<1 = 010
(2) 110 ^ 010 = 100
(110 & 010)<<1 = 100
(3) 100 ^ 100 = 000
(100 & 100)<<1 = 1000
此时进行相加操作就没有进位了,即000 ^ 1000=1000即是最后结果。![]()
![]()
class Solution {
/*
* param a: The first integer
* param b: The second integer
* return: The sum of a and b
*/
public int aplusb(int a, int b) {
while(b != 0){
int carry = a & b;
a = a ^ b;
b = carry << 1;
}
return a;
}
}
![]()
![]()
class Solution {
/*
* param a: The first integer
* param b: The second integer
* return: The sum of a and b
*/
public int aplusb(int a, int b) {
// write your code here, try to do it without arithmetic operators.
if (b == 0) {
return a;
}
int sum = a ^ b;
int carry = (a & b) << 1;
return aplusb(sum, carry);
}
};
![]()
![]()
public class Solution {
/**
* @param str: A string
* @return An integer
*/
public int atoi(String str) {
// write your code here
if (str == null || str.length() < 1)
return 0;
// trim white spaces
str = str.trim();
char flag = '+';
// check negative or positive
int i = 0;
if (str.charAt(0) == '-') {
flag = '-';
i++;
} else if (str.charAt(0) == '+') {
i++;
}
// use double to store result
double result = 0;
// calculate value
while (str.length() > i && str.charAt(i) >= '0' && str.charAt(i) <= '9') {
result = result * 10 + (str.charAt(i) - '0');
i++;
}
if (flag == '-')
result = -result;
// handle max and min
if (result > Integer.MAX_VALUE)
return Integer.MAX_VALUE;
if (result < Integer.MIN_VALUE)
return Integer.MIN_VALUE;
return (int) result;
}
}
![]()
![]()
public class Solution {
//返回第一个重复的,赋值duplicate[0]
public boolean duplicate(int num[],int n,int [] duplicate) {
int[] a = new int[n];
for (int i = 0; i < n; i++) {
if (a[num[i]] != 0) {
duplicate[0] = num[i];
return true;
}
else a[num[i]]++;
}
return false;
}
}
![]()
![]()
//boolean只占一位,所以还是比较省的
public boolean duplicate(int numbers[], int length, int[] duplication) {
boolean[] k = new boolean[length];
for (int i = 0; i < k.length; i++) {
if (k[numbers[i]] == true) {
duplication[0] = numbers[i];
return true;
}
k[numbers[i]] = true;
}
return false;
}
![]()
![]()
public class Solution {
//返回第一个重复的,赋值duplicate[0]
public boolean duplicate(int num[],int n,int [] duplicate) {
for (int i = 0; i < n; i++) {
int index = num[i] >= n ? num[i] - n : num[i];
if (num[index] >= n) {
duplicate[0] = index;
return true;
}
num[index] += n;
}
return false;
}
}
![]()
![]()
public class Solution {
public int[] multiply(int[] A) {
int length = A.length;
int[] B = new int[length];
if(length != 0 ){
B[0] = 1;
//计算下三角连乘
for(int i = 1; i < length; i++){
B[i] = B[i-1] * A[i-1];
}
int temp = 1;
//计算上三角
for(int j = length-2; j >= 0; j--){
temp *= A[j+1];
B[j] *= temp;
}
}
return B;
}
}
![]()
![]()
public class Solution {
//Insert one char from stringstream
char[] ca = new char[256];
StringBuffer sb = new StringBuffer();
public void Insert(char ch)
{
sb.append(ch);
ca[ch]++;
}
//return the first appearence once char in current stringstream
public char FirstAppearingOnce()
{
String str = sb.toString();
for (int i = 0; i < str.length(); i++) {
if (ca[str.charAt(i)] == 1) return str.charAt(i);
}
return '#';
}
}
![]()
![]()
/*
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
*/
public class Solution {
public ListNode EntryNodeOfLoop(ListNode pHead){
if (pHead == null || pHead.next == null) return null;
ListNode slow = pHead;
ListNode fast = pHead.next;
while (slow != fast) {
if (fast == null || fast.next == null) return null;
slow = slow.next;
fast = fast.next.next;
}
while (pHead != slow.next) {
pHead = pHead.next;
slow = slow.next;
}
return pHead;
}
}
![]()
![]()
public class Solution {
public ListNode deleteDuplication(ListNode head){
if (head == null || head.next == null) return head;
ListNode dummy = new ListNode(0);
dummy.next = head;
head = dummy;
while (head.next != null && head.next.next != null) {
if (head.next.val == head.next.next.val) {
int val = head.next.val;
while (head.next != null && head.next.val == val) {
head.next = head.next.next;
}
} else {
head = head.next;
}
}
return dummy.next;
}
}
![]()
![]()
public class Solution {
TreeLinkNode GetNext(TreeLinkNode node)
{
if(node==null) return null;
if(node.right!=null){ //如果有右子树,则找右子树的最左节点
node = node.right;
while(node.left!=null) node = node.left;
return node;
}
while(node.next!=null){ //没右子树,则找第一个当前节点是父节点左孩子的节点
if(node.next.left==node) return node.next;
node = node.next;
}
return null; //退到了根节点仍没找到,则返回null
}
}
![]()
![]()
public class Solution {
boolean isSymmetrical(TreeNode root){
if (root == null) return true;
return helper(root.left, root.right);
}
boolean helper(TreeNode lnode, TreeNode rnode){
if (lnode == null || rnode == null) return lnode == rnode;
if (lnode.val != rnode.val) return false;
return helper(lnode.left, rnode.right) && helper(lnode.right, rnode.left);
}
}
![]()
![]()
public class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) return true;
Stack
![]()
![]()
import java.util.*;
public class Solution {
public ArrayList
![]()
![]()
import java.util.*;
public class Solution {
ArrayList
![]()
![]()
/*
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
/*
算法思想:根据前序遍历规则完成序列化与反序列化。所谓序列化指的是遍历二叉树为字符串;所谓反序列化指的是依据字符串重新构造成二叉树。
依据前序遍历序列来序列化二叉树,因为前序遍历序列是从根结点开始的。当在遍历二叉树时碰到Null指针时,这些Null指针被序列化为一个特殊的字符“#”。
另外,结点之间的数值用逗号隔开。
*/
public class Solution {
int index = -1; //计数变量
String Serialize(TreeNode root) {
StringBuilder sb = new StringBuilder();
if(root == null){
sb.append("#,");
return sb.toString();
}
sb.append(root.val + ",");
sb.append(Serialize(root.left));
sb.append(Serialize(root.right));
return sb.toString();
}
TreeNode Deserialize(String str) {
index++;
//int len = str.length();
//if(index >= len){
// return null;
// }
String[] strr = str.split(",");
TreeNode node = null;
if(!strr[index].equals("#")){
node = new TreeNode(Integer.valueOf(strr[index]));
node.left = Deserialize(str);
node.right = Deserialize(str);
}
return node;
}
}
![]()
![]()
public class Solution {
int cnt = 0;
TreeNode KthNode(TreeNode root, int k){
if (root == null) return root;
TreeNode node = KthNode(root.left, k);
if (node != null) return node;
cnt++;
if (cnt == k) return root;
node = KthNode(root.right, k);
if (node != null) return node;
return null;
}
}
![]()
![]()
链接:https://www.nowcoder.com/questionTerminal/9be0172896bd43948f8a32fb954e1be1
来源:牛客网
private int count = 0;
private PriorityQueue
![]()
![]()
链接:https://www.nowcoder.com/questionTerminal/1624bc35a45c42c0bc17d17fa0cba788
来源:牛客网
/**
* 题目:滑动窗口的最大值
* 思路:滑动窗口应当是队列,但为了得到滑动窗口的最大值,队列序可以从两端删除元素,因此使用双端队列。
* 原则:
* 对新来的元素k,将其与双端队列中的元素相比较
* 1)前面比k小的,直接移出队列(因为不再可能成为后面滑动窗口的最大值了!),
* 2)前面比k大的X,比较两者下标,判断X是否已不在窗口之内,不在了,直接移出队列
* 队列的第一个元素是滑动窗口中的最大值
*/
public class P65_滑动窗口的最大值 {
public ArrayList