剑指offer 剪绳子JZ67
剑指offer 剪绳子
- 目录
- 题目描述
- 题目理解
- 暴力递归无记忆
- 有记忆递归
- 动态规划
目录
本文是参考牛客网的官方题解结合自己理解写的,官方题解:牛客官方题解
题目描述
给你一根长度为n的绳子,请把绳子剪成整数长的m段(m、n都是整数,n>1并且m>1,m<=n),每段绳子的长度记为k[1],…,k[m]。请问k[1]x…xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
输入描述:
输入一个数n,意义见题面。(2 <= n <= 60)
示例:输入 8,输出 18
题目理解
给定一个长度为n(n>1)的绳子,将其分成m段(m>1,m<=n),求m段的乘积最大。
转化成数学上的描述:给定一个数n,求n = a1 + a2 … +am, (m>1)在此条件下, s = a1 * a2 * … * am, s最大
针对本题来说,假如我们用暴力枚举的思路去思考,会出现以下一些问题:
- 这段绳子到底应该分几段,才能得到最优的结果?
- 假设我已经知道了要分m段(假设m已知),那么每段的长度又应该是多少呢?
我们可以从简单的出发,当n的长度为2(2<=n<=60),那么很简单,因为m>1,所以只能分成两段,则s=11=1,再考虑m=3的情况,我们可选的方式是1f(2)以及2f(1)两种情况, f(2)这里可以看做当n=2时,剪绳子所能得到最长的长度,在这里我们已经有两段了满足m>1的情况,那么f(2)就是剩下的一段,我们不剪绳子就是最大的.
同理我们再考虑,m=4,同样1f(3),2f(2),3f(1)三种情况,其中2f(2),f(2)不剪就是最大的.
那么我们再考虑,m=5,1f(4),2f(3),3f(2),4f(1)的三种情况,当我们已经分成两段之后,满足m>1的情况下,f(4),f(3),f(2),f(1)不剪的时候,用数学描述就是:f(n)=n,n<=4,这样递归三部曲的终止条件我们就能知道了.
那我们再考虑n=6,7,8,9,…等情况时,是不是也可以这样拆分呢?以n=6为例,无非就是1f(5),2f(4),3f(3),4f(2),5f(1)等情况罢了,其中f(5),f(4),f(3),f(2),f(1)已经求出来了啊,那么我们直接代进去就可以了啊,这样下一步的递归方式我们也知道了.
暴力递归无记忆
博主之前是学的C++,但是从目前师兄师姐找工作来看还是Java大法好,果断转了Java,牛客上面是C++
import java.util.Scanner;
public class cutRope_JZ67 {
/*暴力递归思想
* 递归函数的设计和功能:back_track(n); 含义是:求长度为n的数,最后分段后的最大乘积,这里我们不需要关心分成多少段
*递归函数的终止条件:m>1,n>1, 如果n=2,back_track(2)=1,n=3,back_track(3)=2,n= 4, 显然back_track(4) = 4,初始条件也就是我们不用计算就能得到的。
*下一步递归:对于长度n,我们需要减少递归参数n,如果第一段为1, 显然下一步递归为back_track(n-1),如果第一段为2, 则下一步递归为
*back_track(n-2)...因为要至少分2段,所以,最后一次可能的情况为最后一段为n-1, 下一步递归为back_track(1),因此,每一步可能的结果为1
* back_track(n-1), 2 * back_track(n-2), ..., (n-1) * back_track(1),在n-1种情况中取一个最大值即可。
* 输入n有2,3,4,5等一系列情况,如果n是2,3,在cut_Rope函数就已经输出了,不会进入递归函数,n等于4,他要划分两段,2*2正好等于4,合并到递归函数里面是一致,
* 在n>4的时候进入递归, 分成两段的情况1*back_track(4),2*back_track(3),back_track(4),back_track(3)肯定是不再分割是最大的
*这里我们不用关系back_track(n-1)等的值为多少,因为最终会递归到我们的终止条件,因此绝对是可以求出来
*/
public int back_track(int n) {
//当进入递归之后,必然是已经剪成两段的,剩下的n=2,3,4不剪就是最好的
//n=4这里是特殊情况,即使剪了2*2就是最大的正好等于本身,所以直接合并到了递归函数里面
if(n<=4) {
return n;
}
int ret=0;
for(int i=1;i<n;++i) {
ret = Math.max(ret,i*back_track(n-i));//此时会循环调用进行比较,back_track(7)会递归到back_track的终止条件back_track(4);
}
return ret;
}
public static void main(String []args) {
System.out.print("Enter a number:");
Scanner sc=new Scanner(System.in);
int number=sc.nextInt();
//初始时,要满足m>1,n=2,3必须剪成两段
if(number==2) {
System.out.print(1);
}
if(number==3) {
System.out.print(2);
}
cutRope_JZ67 a=new cutRope_JZ67();
int output=a.back_track(number);
System.out.print(output);
}
}
有记忆递归
在分析时,我们已经说过,f(5),f(4)这些都已经求过,如下图所示,f(7)的求解拆分,我们有很多重复的,如果还让它一直递归求解这样时间复杂度太高了,我们何不直接开一个数组呢?说干就干
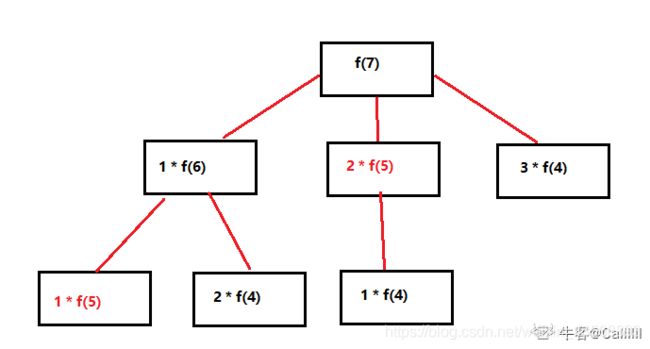 步骤如下:
步骤如下:
初始化一个大小为 n+1 的数组,初始值为 -1 , 也可以-2, 反正是不可能得到的值,这里为什么是n+1呢?,你可以列下比如求解f(6),最后数组记录到就是mark[6],0~6就是n+1.
import java.util.Scanner;
import java.util.Arrays;
/*记忆化递归思想
* 如暴力递归中f(7)是在1*f(6) 2*f(5) 3*f(4)等,其中f(6)的求解是1*f(5),2*f(4)
* 从上面可以看到,f(5),f(4),f(3)会被重复求解,输入数据越大,重复求解次数越多
* 所以考虑开一个数组,将这些已经计算过得数据记录下来
* 递归的理解,当f(7)会一直递归到f(5),f(5)会执行完整个cutRope_Memeory_Recursion函数,到23行mark[5]就会记录下来
* 再依次往上,f(6),f(7)就能在循环函数比较了
* */
public class cutRope_Memeory_Recursion {
public int recur(int n, int[] mark) {
if(n<=4) {
return n;
}
//增加数组记录
if(mark[n]!=-1) {
return mark[n];
}
int ret=0;
for(int i=1;i<n;i++) {
ret=Math.max(ret,i*recur(n-i,mark));
}
mark[n] = ret;
System.out.println("n为: "+ n);
System.out.println("mark为"+mark[n]);
return mark[n];
}
public static void main(String[] args) {
System.out.print("Enter a number:");
Scanner sc1=new Scanner(System.in);
int number=sc1.nextInt();
if(number==2) {
System.out.print(1);
}
if(number==3) {
System.out.print(2);
}
cutRope_Memeory_Recursion cut=new cutRope_Memeory_Recursion();
int[] mark=new int[number+1];
Arrays.fill(mark,-1);//给数组初始化填充一个不可能的结果,可是-2 -3等等
int output=cut.recur(number,mark);
System.out.print(output);
}
}
动态规划
有的书上认为方法二是一种递归版本的动态规划。
所以,我们可以将方法二修改为迭代版本的动态规划。
import java.util.Scanner;
import java.util.Arrays;
/*动态规划只是把上面的递归变成了循环,原理一样
* A:一般,动态规划有以下几种分类:
* 最值型动态规划,比如求最大,最小值是多少
* 计数型动态规划,比如换硬币,有多少种换法
* 坐标型动态规划,比如在m*n矩阵求最值型,计数型,一般是二维矩阵
* 区间型动态规划,比如在区间中求最值
* 可参考 https://www.jianshu.com/p/74fdcae053cf,讲解动态规划的不错
*/
public class cutRope_Dynamic_programming {
public static void main(String[] args) {
System.out.print("Enter a number:");
Scanner sc2=new Scanner(System.in);
int number=sc2.nextInt();
if(number==2) {
System.out.print(1);
}
if(number==3) {
System.out.print(2);
}
int[] mark=new int[number+1];
Arrays.fill(mark,-1);//给数组初始化填充一个不可能的结果,可是-2 -3等等
for(int i=1;i<=4;i++) {
mark[i]=i;
}
for(int i=5;i<=number;i++) {
for(int j=1;j<i;j++) {
mark[i]=Math.max(mark[i],j*mark[i-j]);
}
}
System.out.print(mark[number]);
}
}