[work] Adam优化器
基于随机梯度下降(SGD)的优化算法在科研和工程的很多领域里都是极其核心的。很多理论或工程问题都可以转化为对目标函数进行最小化的数学问题。
按吴恩达老师所说的,梯度下降(Gradient Descent)就好比一个人想从高山上奔跑到山谷最低点,用最快的方式(steepest)奔向最低的位置(minimum)。
SGD基本公式
动量(Momentum)
参考链接:https://distill.pub/2017/momentum/
基本的mini-batch SGD优化算法在深度学习取得很多不错的成绩。然而也存在一些问题需解决:
1. 选择恰当的初始学习率很困难。
2. 学习率调整策略受限于预先指定的调整规则。
3. 相同的学习率被应用于各个参数。
4. 高度非凸的误差函数的优化过程,如何避免陷入大量的局部次优解或鞍点。
自适应优化
AdaGrad
针对简单的SGD及Momentum存在的问题,2011年John Duchi等发布了AdaGrad优化算法(Adaptive Gradient,自适应梯度),它能够对每个不同的参数调整不同的学习率,对频繁变化的参数以更小的步长进行更新,而稀疏的参数以更大的步长进行更新。
公式:
gt表示第t时间步的梯度(向量,包含各个参数对应的偏导数,gt,i表示第i个参数t时刻偏导数)
gt2表示第t时间步的梯度平方(向量,由gt各元素自己进行平方运算所得,即Element-wise)
与SGD的核心区别在于计算更新步长时,增加了分母:梯度平方累积和的平方根。此项能够累积各个参数gt,i的历史梯度平方,频繁更新的梯度,则累积的分母项逐渐偏大,那么更新的步长(stepsize)相对就会变小,而稀疏的梯度,则导致累积的分母项中对应值比较小,那么更新的步长则相对比较大。
AdaGrad能够自动为不同参数适应不同的学习率(平方根的分母项相当于对学习率α进进行了自动调整,然后再乘以本次梯度),大多数的框架实现采用默认学习率α=0.01即可完成比较好的收敛。
优势:在数据分布稀疏的场景,能更好利用稀疏梯度的信息,比标准的SGD算法更有效地收敛。
缺点:主要缺陷来自分母项的对梯度平方不断累积,随之时间步地增加,分母项越来越大,最终导致学习率收缩到太小无法进行有效更新。
RMSProp
RMSProp是Geoffrey Hinton教授在教案中提到的算法,结合梯度平方的指数移动平均数来调节学习率的变化。能够在不稳定(Non-Stationary)的目标函数情况下进行很好地收敛。
Hinton教授讲述RMSProp算法的材料:
http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
计算t时间步的梯度:
计算梯度平方的指数移动平均数(Exponential Moving Average),γ是遗忘因子(或称为指数衰减率),依据经验,默认设置为0.9。
梯度更新时候,与AdaGrad类似,只是更新的梯度平方的期望(指数移动均值),其中ε=10^-8,避免除数为0。默认学习率α=0.001。
优势:能够克服AdaGrad梯度急剧减小的问题,在很多应用中都展示出优秀的学习率自适应能力。尤其在不稳定(Non-Stationary)的目标函数下,比基本的SGD、Momentum、AdaGrad表现更良好。
Adam优化器
2014年12月,Kingma和Lei Ba两位学者提出了Adam优化器,结合AdaGrad和RMSProp两种优化算法的优点。对梯度的一阶矩估计(First Moment Estimation,即梯度的均值)和二阶矩估计(Second
Moment Estimation,即梯度的未中心化的方差)进行综合考虑,计算出更新步长。
主要包含以下几个显著的优点:
1. 实现简单,计算高效,对内存需求少
2. 参数的更新不受梯度的伸缩变换影响
3. 超参数具有很好的解释性,且通常无需调整或仅需很少的微调
4. 更新的步长能够被限制在大致的范围内(初始学习率)
5. 能自然地实现步长退火过程(自动调整学习率)
6. 很适合应用于大规模的数据及参数的场景
7. 适用于不稳定目标函数
8. 适用于梯度稀疏或梯度存在很大噪声的问题
综合Adam在很多情况下算作默认工作性能比较优秀的优化器。
Adam实现原理
算法伪代码:
![]()
Adam更新规则
计算t时间步的梯度:
首先,计算梯度的指数移动平均数,m0 初始化为0。
类似于Momentum算法,综合考虑之前时间步的梯度动量。
β1 系数为指数衰减率,控制权重分配(动量与当前梯度),通常取接近于1的值。
默认为0.9
下图简单展示出时间步1~20时,各个时间步的梯度随着时间的累积占比情况。
其次,计算梯度平方的指数移动平均数,v0初始化为0。
β2 系数为指数衰减率,控制之前的梯度平方的影响情况。
类似于RMSProp算法,对梯度平方进行加权均值。
默认为0.999
第三,由于m0初始化为0,会导致mt偏向于0,尤其在训练初期阶段。
所以,此处需要对梯度均值mt进行偏差纠正,降低偏差对训练初期的影响。
第四,与m0 类似,因为v0初始化为0导致训练初始阶段vt偏向0,对其进行纠正。
第五,更新参数,初始的学习率α乘以梯度均值与梯度方差的平方根之比。
其中默认学习率α=0.001
ε=10^-8,避免除数变为0。
由表达式可以看出,对更新的步长计算,能够从梯度均值及梯度平方两个角度进行自适应地调节,而不是直接由当前梯度决定。
Adam代码实现
算法思路很清晰,实现比较直观:
代码地址:https://github.com/dream-catcher/learning_blogs/blob/master/Adam_Optimizer/adam_optimizer.py
Adam可视化
notebook试验地址:https://github.com/dream-catcher/learning_blogs/tree/master/Adam_Optimizer
Adam缺陷及改进
虽然Adam算法目前成为主流的优化算法,不过在很多领域里(如计算机视觉的对象识别、NLP中的机器翻译)的最佳成果仍然是使用带动量(Momentum)的SGD来获取到的。Wilson 等人的论文结果显示,在对象识别、字符级别建模、语法成分分析等方面,自适应学习率方法(包括AdaGrad、AdaDelta、RMSProp、Adam等)通常比Momentum算法效果更差。
针对Adam等自适应学习率方法的问题,主要两个方面的改进:
1、解耦权重衰减
在每次更新梯度时,同时对其进行衰减(衰减系数w略小于1),避免产生过大的参数。
在Adam优化过程中,增加参数权重衰减项。解耦学习率和权重衰减两个超参数,能单独调试优化两个参数。
参考链接:http://ruder.io/deep-learning-optimization-2017/index.html
2、修正指数移动均值
最近的几篇论文显示较低的[if !msEquation][endif](如0.99或0.9)能够获得比默认值0.999更佳的结果,暗示出指数移动均值本身可能也包含了缺陷。例如在训练过程中,某个mini-batch出现比较大信息量的梯度信息,但由于这类mini-batch出现频次很少,而指数移动均值会减弱他们的作用(因为当前梯度权重及当前梯度的平方的权重,权重都比较小),导致在这种场景下收敛比较差。
https://openreview.net/pdf?id=ryQu7f-RZ
论文作者提出Adam的变形算法AMSGrad。
AMSGrad 使用最大的来更新梯度,而不像Adam算法中采用历史的指数移动均值来实现。作者在小批量数据集及CIFAR-10上观察到比Adam更佳的效果。
参考资料
http://ruder.io/optimizing-gradient-descent/
http://ruder.io/deep-learning-optimization-2017/index.html
作者:Emerson_G
链接:https://www.jianshu.com/p/aebcaf8af76e
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。
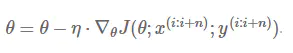

![[work] Adam优化器_第1张图片](http://img.e-com-net.com/image/info8/0f6012dde04649a48786f349492cc825.webp)
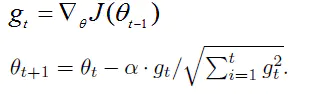

![[work] Adam优化器_第2张图片](http://img.e-com-net.com/image/info8/7529abb6d3314e669a65bb330d9eaf9a.webp)
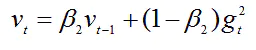
![[work] Adam优化器_第3张图片](http://img.e-com-net.com/image/info8/18982b53dd264cc1a89e2bcc96343ce9.jpg)
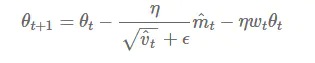
![[work] Adam优化器_第4张图片](http://img.e-com-net.com/image/info8/d994fc31d0964a39b8870fa1fb4ad779.webp)