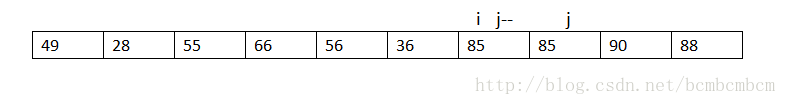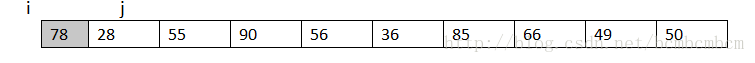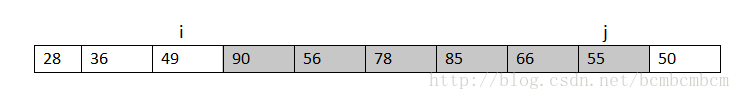快速排序的两种方式及其时间复杂度

首先快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

方法一：

该方法的基本思想是：
1．先从数列中指定一个数作为基准数。
2．进行分区，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
3．再对左右区间重复第二步，直到各区间只有一个数。
设定一个数据源数组dataSource

设定第一个数为中间数，大于此数的放在其右边，小于等于此数的放在其左边。
大致思路是：
首先，我先用一个变量来保存中间数的值及78；

然后设定数组的firstindex为i，lastindex为j，从数组的最后向前遍历，如果发现有小于78的，就使s[i]=s[j],及s[1]=49

数组值改变后，i++;
找到一个小于中间数的值后，再从前往后找大于中间数的值，

找到90大于78，然后让s[j]=90，j--(把这个坑填上，但是前面又有多出一个坑即s[i])    

然后再从后往前找小于78的数，66<78，再赋值，即s[i]=66，i++

再从前往后找大于78的数，85>78,赋值s[j]=85,j--

此刻，i=j,不符合i

此时，小于78的放在了前面，大于78的就被放到了后面，在index i 这分成了两部分，按照上面的步骤，分别对这两部分进行操作即可。
下面上代码：

 //正向想   --- 代码有些啰嗦
   private int[] dataArray = {75,8,55,90,56,36,85,77,49,88};

    public void quicksort(int[] s,int left,int right){
        if (left < right) {
            int i = left, j = right;
            //去第一个数为中间数
            int x = s[left];
            //从后往前找小于 中间数的值，把其放在i的位置
            while (i < j) {
                while (i < j) {
                    if (s[j] < x) {
                        s[i] = s[j];
                        i++;
                        break;
                    }
                    j--;
                }

                //从前向后找大于中间数的值，把其放在j的位置
                while (i < j) {
                    if (s[i] > x) {
                        s[j] = s[i];
                        j--;
                        break;
                    }
                    i++;
                }
            }
            s[i] = x;
            quicksort(s, left, i - 1);
            quicksort(s, i + 1, right);
        }
    }
    //反向想   --- 简化版
    void quick_sort(int s[], int left, int right)
    {
        if (left < right) {
            //第一个数为中间数
            int i = left, j = right, x = s[left];
            while (i < j)
            {
                while(i < j && s[j] >= x) // 从右向左找第一个小于x的数
                    j--;
                if(i < j)
                    //从后往前找小于 中间数的值，把其放在i的位置，然后i+1
                    s[i++] = s[j];

                while(i < j && s[i] < x) // 从左向右找第一个大于等于x的数
                    i++;
                if(i < j)
                    //从前向后找大于中间数的值，把其放在j的位置,然后 j-1
                    s[j--] = s[i];
            }
            s[i] = x;
            quick_sort(s, left, i - 1); // 递归调用
            quick_sort(s, i + 1, right);
        }
    }

  @Test
    public void testSort(){

        quicksort(dataArray,0,dataArray.length-1);

        for (int k = 0;kout.println(dataArray[k]);
        }
    }

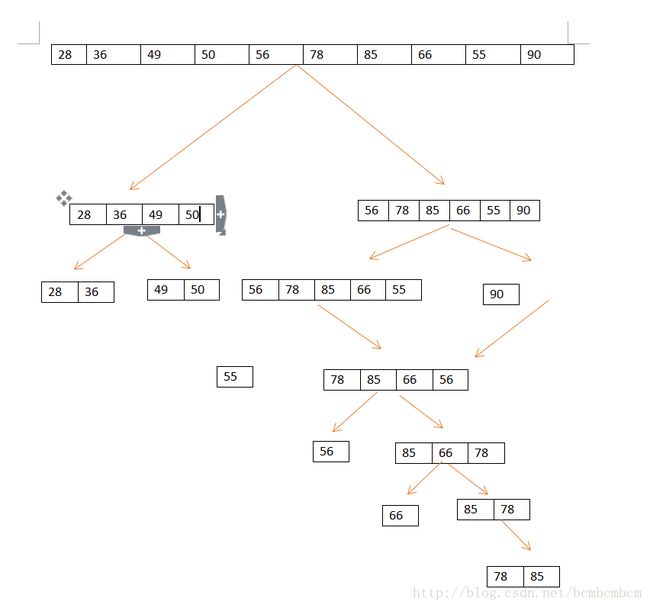
方法二：

找到符合的就交换  而不是把中间数记录下来
设置数组的最后一个数是中间数。
i = (firstIndex)left - 1;
j = (firstIndex)left

s[i]=78>50,不交换，j++；

28<50,i++,交换，j++,

55>50,不交换，j++;

90>50,不交换，j++;

56>50,不交换,j++

36<50,i++，交换，j++;

此时，小于50的放在了前面，大于50的就被放到了后面，在index i 这分成了两部分，按照上面的步骤，分别对这两部分进行操作即可。
下面上代码

 // 交换版 ---  找到符合的就交换  而不是把中间数记录下来
    public  void swap(int s[],int i,int j){
        int temp;
        temp = s[i];
        s[i] = s[j];
        s[j] = temp;
    }

    public void quick__sork(int s[], int left, int right){
        if (left < right) {
            //最后一个数为中间数
            int i = left-1, j = left;
            //i是最后一个小于中间数的值
            //一进循环，先使 i+1                                                                                  
            //使i 一直是 第一个大于中间数 的值，只要找到小于中间数的，就和s[i]交换
            while (j<=right) {
                if (s[j]<=s[right]){
                    i++;
                    swap(s,i,j);
                }
                j++;
            }
            quick__sork(s,left,i-1);
            quick__sork(s,i+1,right);
        }

    }

三、时间复杂度

快速排序的最好情况：O(nlog n),最坏情况：O(n^2)
最好情况：每次都恰好五五分，一次递归共需比较n次，递归深度为log n
最坏情况：已排序数组，比较次数为n-1+n-2+...+1=n*(n-1)/2 ~1*n^2/2

参考：
这里写链接内容
这里写链接内容