【2019/08/24测试 T2】数学课

传送门

---

Problem

给定一个包含 $n$ 个元素的集合 $P=\{1,2,3,...,n\}$，求有多少个集合 $A\subseteq P$，满足任意 $x\in A$ 有 $2x\notin A$，且对于 $A$ 在 $P$ 中的补集 $B$，也满足任意 $x\in B$ 有 $2x\notin B$。

有 $q$ 个询问，每次给出一个整数 $m$，询问大小为 $m$ 的集合有多少个。

答案对 $10000019$ 取模。

数据范围：$n,m\le 10^{18}$，$q\le 100000$。

---

Solution

这道题在考场上只想到了 $O(n)$ 的做法，拿了 $80$ 分。

我们以 $n=10$ 为例来讲一下这道题吧。

我们把这十个数分成若干条链，每个数都与它的两倍相连，得到下图。

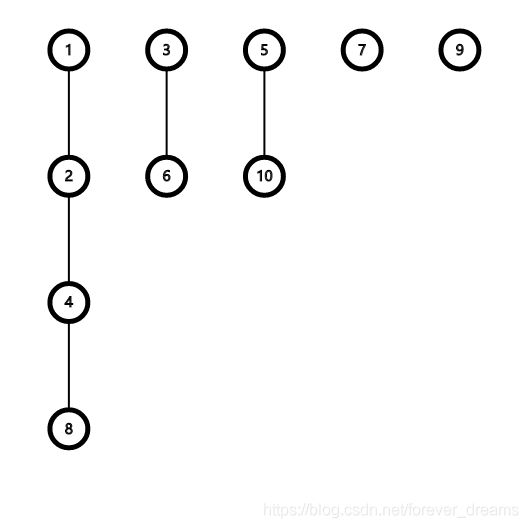
那么根据题意，相邻的两个点中必须选一个。

我们设链长为 $l$。对于一条长度为偶数的链，它对 $A$ 集合有 $\frac{l}{2}$ 的贡献，有两种选择情况。对于一条长度为奇数的链，可以把链头取出来，剩下的就是偶链的情况了，而且链头可以随意选 $A$ 或者 $B$。

假设我们有 $c_1$ 条偶链，$c_2$ 条奇链，且当前询问的是 $m$，那么答案就是：

$$ans=2^{c_1}\left(\genfrac{}{}{0ex}{}{c_2}{m-\frac{c_1}{2}}\right)$$

由于模数 $P$ 比较小，可以用 lucas 定理来解决上式的组合数。

现在的问题就是怎么统计奇链和偶链的数量。

我们不妨枚举链长，那么对于一个长度为 $l$ 的链，如果链头是 $x$，那么有：

$$\{\begin{array}{l}x\cdot 2^{l-1}\le n\\ x\cdot 2^l>n\end{array}$$

解出来就是 $\frac{n}{2^l}<x\le \frac{n}{2^{l-1}}$，我们只需要这个范围内的奇数，分类讨论以下即可。

PS：这道题不好讲清楚，可以自己想一想，捋捋思路。

---

Code

#include
#include
#include
#define P 10000019
#define ll long long
using namespace std;
ll n,sum=0,A=0;
int q,temp=1,fac[P],ifac[P];
int add(int x,int y)  {return x+y>=P?x+y-P:x+y;}
int dec(int x,int y)  {return x-y< 0?x-y+P:x-y;}
int mul(int x,int y)  {return 1ll*x*y%P;}
int power(int a,int b,int ans=1){
	for(;b;b>>=1,a=mul(a,a))
		if(b&1)  ans=mul(ans,a);
	return ans;
}
int prework(){
	fac[0]=fac[1]=1;
	for(int i=2;i<P;++i)  fac[i]=mul(fac[i-1],i);
	ifac[P-1]=power(fac[P-1],P-2);
	for(int i=P-2;~i;--i)  ifac[i]=mul(ifac[i+1],i+1);
}
int C(int n,int m){
	if(n<m)  return 0;
	return mul(fac[n],mul(ifac[m],ifac[n-m]));
}
int Lucas(ll n,ll m){
	if(!m)  return 1;
	return mul(C(n%P,m%P),Lucas(n/P,m/P));
}
ll calc(ll l,ll r)  {return (r-l+1)/2+((l&1)&&(r&1));}
int Query(ll x){
	if(x<A||x>A+sum)  return 0;
	return mul(temp,Lucas(sum,x-A));
}
int main(){
	prework();
	scanf("%lld%d",&n,&q);
	for(int i=1;(1ll<<(i-1))<=n;++i){
		ll l=n/(1ll<<i)+1,r=n/(1ll<<(i-1)),num=calc(l,r);
		A+=(i/2)*num,(i&1)?sum+=num:temp=mul(temp,power(2,num%(P-1)));
	}
	ll x;
	while(q--){
		scanf("%lld",&x);
		printf("%d\n",Query(x));
	}
	return 0;
}