论文阅读笔记《Memory In Memory: A Predictive Neural Network...》
不断更新中…
文章目录
- 0 摘要与介绍
- 时空序列预测任务定义
- 要解决的问题
- 定位造成这个问题的原因
- 解决问题的方案
- *关于MIM,扯得详细点*
- 实验结果咋样
- 1 相关工作
- 1.1 ARIMA
- 1.2 Deterministic Spatiotemporal Prediction
- 2 模型
- 2.1 ST-LSTM
- 2.2 Zigzag架构(Z字形架构)
- 2.3 MIM块
我已经代码复现,并进行了详细的公式推导,结论是这篇文章并无工程价值。作者官方代码和论文有差距,而且大量trick,模型也复杂,不适合工程化
0 摘要与介绍
时空序列预测任务定义
作者认为自然界中的时空序列预测问题很多都是高度非平稳(highly non-stationary) 的随机过程(即随机过程的统计特性随时间的推移而变化),不过根据Cramer的分解公式,任一非平稳的随机过程可以被分解为确定的,时变的多项式加上一个均值为0的随机项(看看这里)。通过应用不同的适当的操作,作者认为可以将时变的多项式转化为一个常量,使得确定性的部分具有可预测性。
要解决的问题
作者认为以前的LSTM魔改网络(如PredRNN)缺少对非平稳信息的建模让网络很难有着时空动力学的推理能力,造成预测图片模糊。说明白点,就是作者认为大多数用来做时空序列预测的循环神经网络的状态转移函数太简单了 ,阻止它们学习到更多的时空信息。
定位造成这个问题的原因
作者观察到在降水预测任务中,PredRNN中80%的遗忘门在所有时间步骤中都是饱和的,即没怎么随时间变化。(通过实验观测发现)
解决问题的方案
因此作者提出了一个Memory In Memory(MIM) 单元(把LSTM内遗忘门改了, 换成这玩意),并用于循环网络架构中。MIM单元会去学习两个相邻RNN神经元隐状态之间的微分信号来模拟时空序列中平稳与非平稳的特性。说得简单明白点,就是差分的思想,因为经典时间序列分析中的大多数统计预测方法都假设通过执行适当的变换(如差分)可以使非平稳趋势近似平稳。
关于MIM,扯得详细点
1 隐藏状态包含前后时间步骤图片的差分信息,而不光是卷积提取特征生成特征图就完事了
2 作者网络架构中叠加了多个MIM单元(就是深层RNN网络)
3 作者同时认为过度差分会导致信息的损失,所以只对遗忘门(处理的是memory)下手,没有对所有的LSTM门控单元下手
4 遗忘门被换成了两个模块
实验结果咋样
这么一搞,调参之后在人工合成数据集(MovingMNIST)和实际数据集(雷达回波,Human 3.6M)上实验结果达到2019年的state of the art了,就有了这篇论文。
1 相关工作
1.1 ARIMA
AutoRegression Integrated Moving Average(自回归移动平均模型)
它把power spectrum随时间保持不变的时间序列随机变量看作是信号和噪声的组合。ARIMA模型旨在将信号与噪声分离, 然后将获得的信号进行预测。从理论上讲,它通过差分将非平稳过程转化为平稳过程来处理时间序列预测。这也是这篇论文差分思想的来源。
1.2 Deterministic Spatiotemporal Prediction
确定性时空预测
研究历史(我自己也做了补充):
RNN -> Seq2Seq+LSTM -> ConvLSTM -> ConvLSTM+Optical flow(结合了传统光流法) -> Encoder Forecaster+TrajGRU(卷积前先做grid sample采样,相当于网络本身可以学习卷积连接结构) -> Video Pixel Network -> ConvLSTM+zigzag memory flow架构(PredRNN, 即ST-LSTM) -> Adversarial Learning (走的GAN的路子,主要想解决预测序列模糊的问题)
2 模型
2.1 ST-LSTM
要想理解MIM,一定要先理解PredRNN,
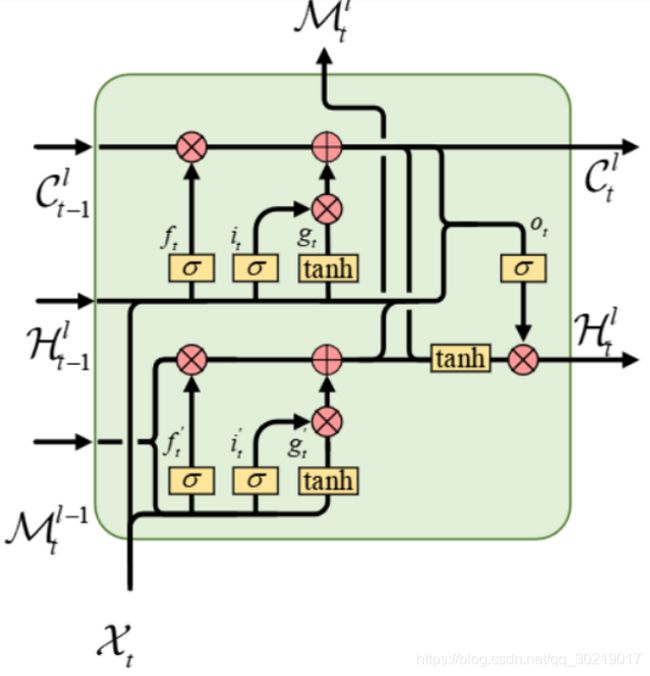
PredRNN中的神经元叫做ST-LSTM,结构如下图(原论文那个图实在是不好理解,用了网上找到的别人画的图)
i t ′ = σ ( W i ′ ∗ [ X t , M t l − 1 ] ) f t ′ = σ ( W f ′ ∗ [ X t , M t l − 1 ] ) g t ′ = tanh ( W g ′ ∗ [ X t , M t l − 1 ] ) M t l = f t ′ ⊙ M t l − 1 + i t ′ ⊙ g t ′ i_t' = \sigma(\mathcal{W}_i' * [\mathcal{X}_t, \mathcal{M}_t^{l-1}]) \\ f_t' = \sigma(\mathcal{W}_f' * [\mathcal{X}_t, \mathcal{M}_t^{l-1}]) \\ g_t' = \tanh(\mathcal{W}_g' * [\mathcal{X}_t, \mathcal{M}_t^{l-1}]) \\ \mathcal{M}_t^l = f_t' \odot \mathcal{M}_t^{l-1} + i_t' \odot g_t' it′=σ(Wi′∗[Xt,Mtl−1])ft′=σ(Wf′∗[Xt,Mtl−1])gt′=tanh(Wg′∗[Xt,Mtl−1])Mtl=ft′⊙Mtl−1+it′⊙gt′
这四个公式刻画了下面的那块lstm干的事情,加个括号代表张量拼接(concatenate),计算了i, f, g三个门状态后,cell state( M t l \mathcal{M}_t^l Mtl)向上流了。但你会觉得很奇怪,说怎么没有输出门(o), 而且向右传的hidden state去哪了呢?
这里,下面那个lstm单元是没有输出门的,至于向右传递的隐状态,靠待会的一个公式(会把 M t l \mathcal{M}_t^l Mtl代入进去)。
所以懂了吧,对下面的LSTM单元来说,输出门被取消, M t l \mathcal{M}_t^l Mtl承担了普通LSTM单元里cell state和hidden state的职责。下面的神经元处理的是竖直方向上的空间信息(它会不断向上传递)。
再来看上面那块LSTM:
i t = σ ( W i ∗ [ X t , H t − 1 l ] ) f t = σ ( W f ∗ [ X t , H t − 1 l ] ) g t = tanh ( W g ∗ [ X t , H t − 1 l ] ) C t l = f t ⊙ C t − 1 l + i t ⊙ g t i_t = \sigma(\mathcal{W}_i * [\mathcal{X}_t, \mathcal{H}_{t-1}^l]) \\ f_t = \sigma(\mathcal{W}_f * [\mathcal{X}_t, \mathcal{H}_{t-1}^l]) \\ g_t = \tanh(\mathcal{W}_g * [\mathcal{X}_t, \mathcal{H}_{t-1}^l]) \\ \mathcal{C}_t^l = f_t \odot \mathcal{C}_{t-1}^l + i_t \odot g_t it=σ(Wi∗[Xt,Ht−1l])ft=σ(Wf∗[Xt,Ht−1l])gt=tanh(Wg∗[Xt,Ht−1l])Ctl=ft⊙Ct−1l+it⊙gt
对嘛,这四个公式,和普通的LSTM一丁点区别都没有!
但是上面那块LSTM还承担着作为整体ST-LSTM的向右传递信息的职责:
ST-LSTM整体的输出门与向右传递的hidden state:
o t = σ ( W o ∗ [ X t , H t − 1 l , C t l , M t l ] ) H t l = o t ⊙ tanh ( W 1 × 1 ∗ [ C t l , M t l ] ) o_t = \sigma(\mathcal{W}_o * [\mathcal{X}_t, \mathcal{H}_{t-1}^l, \mathcal{C}_t^l, \mathcal{M}_t^l]) \\ \mathcal{H}_t^l = o_t \odot \tanh(\mathcal{W}_{1 \times 1} * [\mathcal{C}_t^l, \mathcal{M}_t^l]) ot=σ(Wo∗[Xt,Ht−1l,Ctl,Mtl])Htl=ot⊙tanh(W1×1∗[Ctl,Mtl])
分析下吧:
C t l \mathcal{C}_t^l Ctl是上面那块LSTM的cell state(关于时间信息的长期记忆), M t l \mathcal{M_t^l} Mtl是下面那块LSTM的cell state(关于空间信息的长期记忆)
X t \mathcal{X}_t Xt与 H t − 1 l \mathcal{H}_{t-1}^l Ht−1l就不说了,两个主要的输入(分别代表空间信息与时间信息)。
那现在的 o t o_t ot代表了啥,对 1 时空输入与 2 本单元产生的时空长期记忆的【输出门状态】,
H t l \mathcal{H}_t^l Htl代表了啥,流向下一个时间步骤的同层神经元的时空信息。
对ST-LSTM的总结如下:
1 下方LSTM的长期记忆 M t l \mathcal{M}_t^l Mtl往上层与右方流动,没有输出门,也没有向右输出的短期记忆
2 上方LSTM的计算与普通LSTM无异,长期记忆 C t l \mathcal{C}_t^l Ctl流向右方
3 整体ST-LSTM向右传递的短期记忆(也是上方LSTM的短期记忆) H t l \mathcal{H}_t^l Htl是个大杂烩,包含了两个输入和上下两个单元的长期记忆
一通百通,慢慢多看两遍我的叙述,肯定能明白的
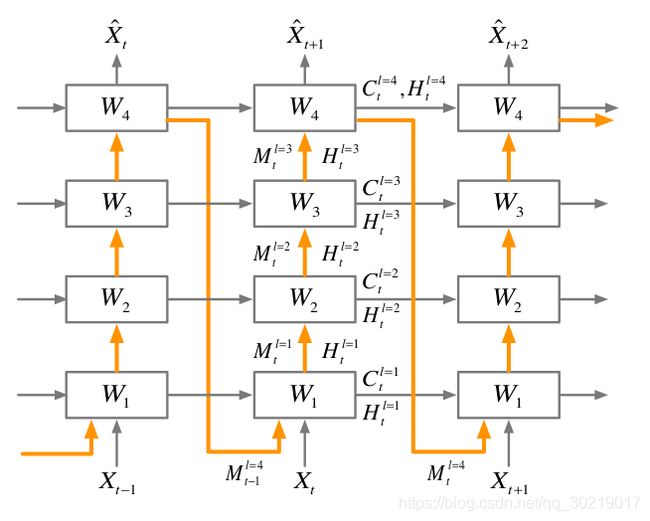
2.2 Zigzag架构(Z字形架构)
在单向深度循环神经网络的基础上, M t l \mathcal{M}_t^l Mtl 承担了从上流动再传输给下一个时间步骤最底层的神经元的职责
说完了PredRNN, 接下来说MIM:
2.3 MIM块
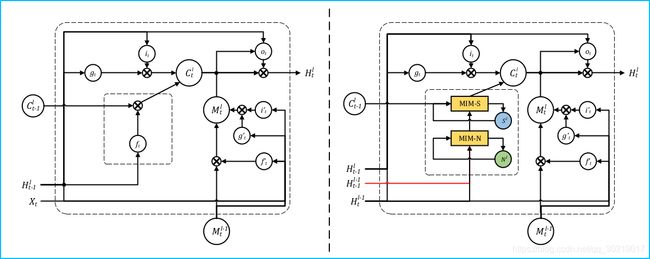
如图, 左边是正常的LSTM单元,右边是嵌入MIM块的LSTM单元。注意, X t X_t Xt 被替换成了 H t l − 1 H_t^{l-1} Htl−1,代表MIM块没法用于网络第一层。MIM-N用来处理non-stationary(非平稳)的信息,MIM-S用来处理stationary的信息。举个例子,假设这个网络正在处理一个视频序列,里面是一个行人以常速行走,那么他的速度可以被视为一个平稳过程的信息,他的摇动腿等动作可以被视为非平稳过程信息(显然很难被预测)。然而传统的LSTM-like网络的遗忘门几乎只学到了平稳过程的信息,遗忘门经常处于饱和状态。
MIM-N的输入包含了 H t − 1 l − 1 H_{t-1}^ {l-1} Ht−1l−1 和 H t l − 1 H_{t}^{l-1} Htl−1 , 捕获下面一层两个时间状态间的差分信息 ( H t l − 1 − H t − 1 l − 1 ) (H_{t}^{l-1}-H_{t-1}^{l-1}) (Htl−1−Ht−1l−1), 产生一个输出 D t l \mathcal{D}_t^l Dtl
MIM-S的输入包含了这个 D t l \mathcal{D}_t^l Dtl和本层前一个时间状态传递来的cell state: C t − 1 l C_{t-1}^l Ct−1l,用来捕获平稳过程信息