沉淀、分享、成长,让自己和他人都能有所收获!
一、前言
算法是数据结构的灵魂!
好的算法搭配上合适的数据结构,可以让代码功能大大的提升效率。当然,算法学习不只是刷题,还需要落地与应用,否则到了写代码的时候,还是会for循环+ifelse。
当开发一个稍微复杂点的业务流程时,往往要用到与之契合的数据结构和算法逻辑,在与设计模式结合,这样既能让你的写出具有高性能的代码,也能让这些代码具备良好的扩展性。
在以往的章节中,我们把Java常用的数据结构基本介绍完了,都已收录到:跳转 -> 《面经手册》,章节内容下图;

那么,有了这些数据结构的基础,接下来我们再学习一下Java中提供的算法工具类,Collections。
二、面试题
谢飞机,今天怎么无精打采的呢,还有黑眼圈?
答:好多知识盲区呀,最近一直在努力补短板,还有面经手册里的数据结构。
问:那数据结构看的差不多了吧,你有考虑过,数据结构里涉及的排序、二分查找吗?
答:二分查找会一些,巴拉巴拉。
问:还不错,那你知道这个方法在Java中有提供对应的工具类吗?是哪个!
答:这!?好像没注意过,没用过!
问:去吧,回家在看看书,这两天也休息下。
飞机悄然的出门了,但这次面试题整体回答的还是不错的,面试官决定下次再给他一个机会。
三、Collections 工具类
java.util.Collections,是java集合框架的一个工具类,主要用于Collection提供的通用算法;排序、二分查找、洗牌等算法操作。
从数据结构到具体实现,再到算法,整体的结构如下图;
1. Collections.sort 排序
1.1 初始化集合
List list = new ArrayList();
list.add("7");
list.add("4");
list.add("8");
list.add("3");
list.add("9");
1.2 默认排列[正序]
Collections.sort(list);
// 测试结果:[3, 4, 7, 8, 9]
1.3 Comparator排序
Collections.sort(list, new Comparator() {
@Override
public int compare(String o1, String o2) {
return o2.compareTo(o1);
}
});
- 我们使用
o2与o1做对比,这样会出来一个倒叙排序。 - 同时,
Comparator还可以对对象类按照某个字段进行排序。 - 测试结果如下;
[9, 8, 7, 4, 3]
1.4 reverseOrder倒排
Collections.sort(list, Collections.reverseOrder());
// 测试结果:[9, 8, 7, 4, 3]
Collections.的源码部分就和我们上面把两个对比的类调换过来一样。reverseOrder() c2.compareTo(c1);
1.5 源码简述
关于排序方面的知识点并不少,而且有点复杂。本文主要介绍 Collections 集合工具类,后续再深入每一个排序算法进行讲解。
Collections.sort
集合排序,最终使用的方法:Arrays.sort((E[]) elementData, 0, size, c);
public static void sort(T[] a, int fromIndex, int toIndex,
Comparator c) {
if (c == null) {
sort(a, fromIndex, toIndex);
} else {
rangeCheck(a.length, fromIndex, toIndex);
if (LegacyMergeSort.userRequested)
legacyMergeSort(a, fromIndex, toIndex, c);
else
TimSort.sort(a, fromIndex, toIndex, c, null, 0, 0);
}
}
- 这一部分排序逻辑包括了,旧版的归并排序
legacyMergeSort和TimSort排序。 - 但因为开关的作用,
LegacyMergeSort.userRequested = false,基本都是走到TimSort排序 。 - 同时在排序的过程中还会因为元素的个数是否大于
32,而选择分段排序和二分插入排序。这一部分内容我们后续专门在排序内容讲解
2. Collections.binarySearch 二分查找
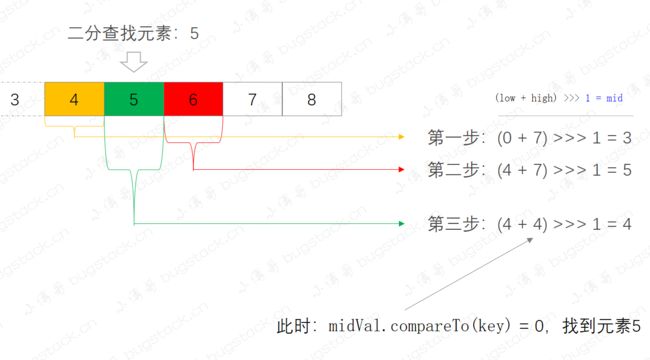
- 看到这张图熟悉吗,这就是集合元素中通过二分查找定位指定元素5。
- 二分查找的前提是集合有序,否则不能满足二分算法的查找过程。
- 查找集合元素5,在这个集合中分了三部;
- 第一步,
(0 + 7) >>> 1 = 3,定位list.get(3) = 4,则继续向右侧二分查找。 - 第二步,
(4 + 7) >>> 1 = 5,定位list.get(5) = 6,则继续向左侧二分查找。 - 第三步,
(4 + 4) >>> 1 = 4,定位list.get(4) = 5,找到元素,返回结果。
- 第一步,
2.1 功能使用
@Test
public void test_binarySearch() {
List list = new ArrayList();
list.add("1");
list.add("2");
list.add("3");
list.add("4");
list.add("5");
list.add("6");
list.add("7");
list.add("8");
int idx = Collections.binarySearch(list, "5");
System.out.println("二分查找:" + idx);
}
- 此功能就是上图中的具体实现效果,通过
Collections.binarySearch定位元素。 - 测试结果:
二分查找:4
2.2 源码分析
Collections.binarySearch
public static int binarySearch(List> list, T key) {
if (list instanceof RandomAccess || list.size() 这段二分查找的代码还是蛮有意思的,list instanceof RandomAccess 这是为什么呢?因为 ArrayList 有实现 RandomAccess,但是 LinkedList 并没有实现这个接口。同时还有元素数量阈值的校验 BINARYSEARCH_THRESHOLD = 5000,小于这个范围的都采用 indexedBinarySearch 进行查找。那么这里其实使用 LinkedList 存储数据,在元素定位的时候,需要get循环获取元素,就会比 ArrayList 更耗时。
Collections.indexedBinarySearch(list, key):
private static int indexedBinarySearch(List> list, T key) {
int low = 0;
int high = list.size()-1;
while (low <= high) {
int mid = (low + high) >>> 1;
Comparable midVal = list.get(mid);
int cmp = midVal.compareTo(key);
if (cmp < 0)
low = mid + 1;
else if (cmp > 0)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found
}
以上这段代码就是通过每次折半二分定位元素,而上面所说的耗时点就是list.get(mid),这在我们分析数据结构时已经讲过。《LinkedList插入速度比ArrayList快?你确定吗?》
Collections.iteratorBinarySearch(list, key):
private static int iteratorBinarySearch(List> list, T key)
{
int low = 0;
int high = list.size()-1;
ListIterator> i = list.listIterator();
while (low <= high) {
int mid = (low + high) >>> 1;
Comparable midVal = get(i, mid);
int cmp = midVal.compareTo(key);
if (cmp < 0)
low = mid + 1;
else if (cmp > 0)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found
}
上面这段代码是元素数量大于5000个,同时是 LinkedList 时会使用迭代器 list.listIterator 的方式进行二分查找操作。也算是一个优化,但是对于链表的数据结构,仍然没有数组数据结构,二分处理的速度快,主要在获取元素的时间复杂度上O(1) 和 O(n)。
3. Collections.shuffle 洗牌算法
洗牌算法,其实就是将 List 集合中的元素进行打乱,一般可以用在抽奖、摇号、洗牌等各个场景中。
3.1 功能使用
Collections.shuffle(list);
Collections.shuffle(list, new Random(100));
它的使用方式非常简单,主要有这么两种方式,一种直接传入集合、另外一种还可以传入固定的随机种子这种方式可以控制洗牌范围范围
3.2 源码分析
按照洗牌的逻辑,我们来实现下具体的核心逻辑代码,如下;
@Test
public void test_shuffle() {
List list = new ArrayList();
list.add("1");
list.add("2");
list.add("3");
list.add("4");
list.add("5");
list.add("6");
list.add("7");
list.add("8");
Random random = new Random();
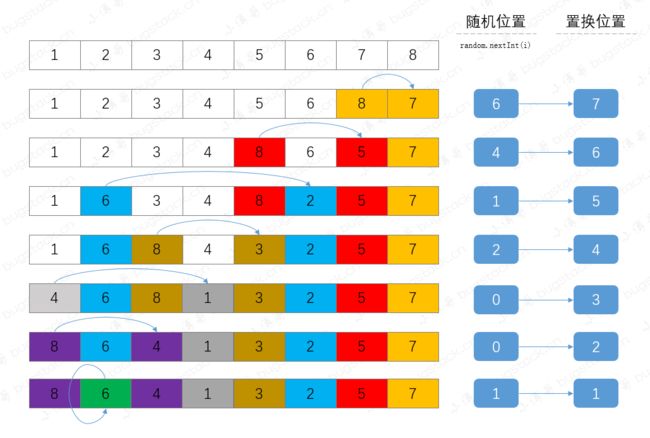
for (int i = list.size(); i > 1; i--) {
int ri = random.nextInt(i); // 随机位置
int ji = i - 1; // 顺延
System.out.println("ri:" + ri + " ji:" + ji);
list.set(ji, list.set(ri, list.get(ji))); // 元素置换
}
System.out.println(list);
}
运行结果:
ri:6 ji:7
ri:4 ji:6
ri:1 ji:5
ri:2 ji:4
ri:0 ji:3
ri:0 ji:2
ri:1 ji:1
[8, 6, 4, 1, 3, 2, 5, 7]
这部分代码逻辑主要是通过随机数从逐步缩小范围的集合中找到对应的元素,与递减的下标位置进行元素替换,整体的执行过程如下;
4. Collections.rotate 旋转算法
旋转算法,可以把ArrayList或者Linkedlist,从指定的某个位置开始,进行正旋或者逆旋操作。有点像把集合理解成圆盘,把要的元素转到自己这,其他的元素顺序跟随。
4.1 功能应用
List list = new ArrayList();
list.add("7");
list.add("4");
list.add("8");
list.add("3");
list.add("9");
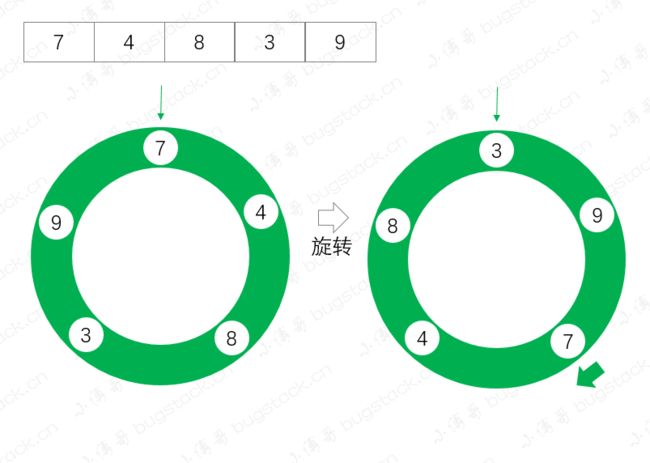
Collections.rotate(list, 2);
System.out.println(list);
这里我们将集合顺序;7、4、8、3、9,顺时针旋转2位,测试结果如下;逆时针旋转为负数
测试结果
[3, 9, 7, 4, 8]
通过测试结果我们可以看到,从元素7开始,正向旋转了两位,执行效果如下图;
4.2 源码分析
public static void rotate(List list, int distance) {
if (list instanceof RandomAccess || list.size() < ROTATE_THRESHOLD)
rotate1(list, distance);
else
rotate2(list, distance);
}
关于旋转算法的实现类分为两部分;
- Arraylist 或者元素数量不多时,
ROTATE_THRESHOLD = 100,则通过算法rotate1实现。 - 如果是 LinkedList 元素数量又超过了 ROTATE_THRESHOLD,则需要使用算法
rotate2实现。
那么,这两个算法有什么不同呢?
4.2.1 旋转算法,rotate1
private static void rotate1(List list, int distance) {
int size = list.size();
if (size == 0)
return;
distance = distance % size;
if (distance < 0)
distance += size;
if (distance == 0)
return;
for (int cycleStart = 0, nMoved = 0; nMoved != size; cycleStart++) {
T displaced = list.get(cycleStart);
int i = cycleStart;
do {
i += distance;
if (i >= size)
i -= size;
displaced = list.set(i, displaced);
nMoved ++;
} while (i != cycleStart);
}
}
这部分代码看着稍微多一点,但是数组结构的操作起来并不复杂,基本如上面圆圈图操作,主要包括以下步骤;
distance = distance % size;,获取旋转的位置。- for循环和dowhile,配合每次的旋转操作,比如这里第一次会把0位置元素替换到2位置,接着在dowhile中会判断
i != cycleStart,满足条件继续把替换了2位置的元素继续往下替换。直到一轮循环把所有元素都放置到正确位置。 - 最终list元素被循环替换完成,也就相当从某个位置开始,正序旋转2个位置的操作。
4.2.2 旋转算法,rotate2
private static void rotate2(List list, int distance) {
int size = list.size();
if (size == 0)
return;
int mid = -distance % size;
if (mid < 0)
mid += size;
if (mid == 0)
return;
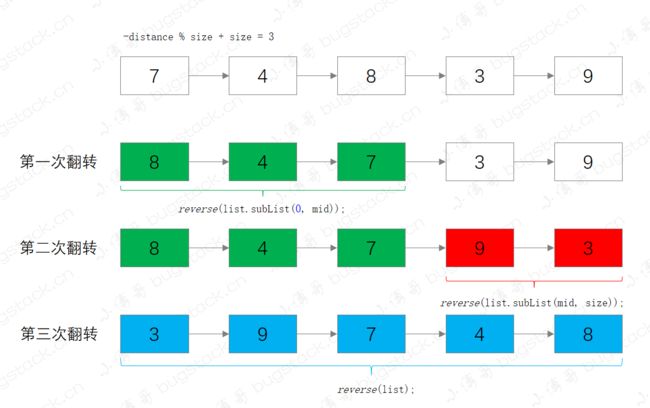
reverse(list.subList(0, mid));
reverse(list.subList(mid, size));
reverse(list);
}
接下来这部分源码主要是针对大于100个元素的LinkedList进行操作,所以整个算法也更加有意思,它的主要操作包括;
- 定位拆链位置,-distance % size + size,也就是我们要旋转后找到的元素位置
- 第一次翻转,把从位置0到拆链位置
- 第二次翻转,把拆链位置到结尾
- 第三次翻转,翻转整个链表
整体执行过程,可以参考下图,更方便理解;
5. 其他API介绍
这部分API内容,使用和设计上相对比较简单,平时可能用的时候不多,但有的小伙伴还没用过,就当为你扫盲了。
5.1 最大最小值
String min = Collections.min(Arrays.asList("1", "2", "3"));
String max = Collections.max(Arrays.asList("1", "2", "3"));
Collections工具包可以进行最值的获取。
5.2 元素替换
List list = new ArrayList();
list.add("7");
list.add("4");
list.add("8");
list.add("8");
Collections.replaceAll(list, "8", "9");
// 测试结果: [7, 4, 9, 9]
- 可以把集合中某个元素全部替换成新的元素。
5.3 连续集合位置判断
@Test
public void test_indexOfSubList() {
List list = new ArrayList();
list.add("7");
list.add("4");
list.add("8");
list.add("3");
list.add("9");
int idx = Collections.indexOfSubList(list, Arrays.asList("8", "3"));
System.out.println(idx);
// 测试结果:2
}
在使用String操作中,我们知道"74839".indexOf("8");,可以获取某个元素在什么位置。而在ArrayList集合操作中,可以获取连续的元素,在集合中的位置。
5.4 synchronized
List list = Collections.synchronizedList(new ArrayList());
Map map = Collections.synchronizedMap(new HashMap());
- 这个很熟悉吧,甚至经常使用,但可能会忽略这些线程安全的方法来自于
Collections集合工具包。
四、总结
- 本章节基本将
java.util.Collections工具包中的常用方法介绍完了,以及一些算法的讲解。这样在后续需要使用到这些算法逻辑时,就可以直接使用并不需要重复造轮子。 - 学习数据结构、算法、设计模式,这三方面的知识,重点还是能落地到日常的业务开发中,否则空、假、虚,只能适合吹吹牛,并不会给项目研发带来实际的价值。
- 懂了就是真的懂,别让自己太难受。死记硬背谁也受不了,耗费了大量的时间,知识也没有吸收,学习一个知识点最好就从根本学习,不要心浮气躁。
五、系列推荐
- DDD领域驱动设计落地方案
- 重学Java设计模式(22个真实开发场景)
- 面经手册(上最快的车,拿最贵的offer)
- 字节码编程(非入侵式全链路监控实践)