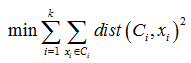聚类篇——（二）K-means聚类

上一篇博文介绍了什么是聚类分析以及其应用场景，本篇博文详细介绍常用聚类算法之一K-means聚类，将从以下几个方面展开介绍：

• K-means聚类基本思想及其优缺点，初步了解K-means聚类；
• K-means聚类逻辑计算过程，了解其内部实现逻辑；
• K-means聚类初始中心点选择的合理性，会直接影响聚类收敛和效果，详细介绍最大距离法、最大最小距离法、Huffman树三种确定初始中心点的方法；
• K-means聚类应用示例。

1. K-means聚类概述

K-means聚类也称快速聚类，属于覆盖型数值划分聚类算法。它得到的聚类结果，每个样本点都唯一属于一个类，而且聚类变量为数值型，并采用划分原理进行聚类。K-means聚类涉及两个主要方面的问题：第一，如何测度样本的“亲疏程度”；第二，如何进行聚类。
K-means聚类的基本思想：参数K用以决定结果中簇的数目，算法开始时，要在数据集中随机选择K个数据对象用来当做K个簇的初始中心，而将剩下的各个数据对象根据他们和每个聚类簇心的距离选择簇心最近的簇分配到其中。然后重新计算各个聚类簇中的所有数据对象的平均值，并将得到的结果作为新的簇心；逐步重复上述过程直至目标函数收敛为止。

K-means聚类算法的优缺点

• 优点：K均值算法伸缩性良好，且针对大型数据集效率高。
• 缺点：(1)初始聚类中心选择的好与坏将会对聚类结果的质量产生很大影响；(2)算法很容易陷入局部最优解，有时会产生较差的结果；(3)算法开始时要求用户给出聚类簇的个数K，而对于K值的选择还没有很好的准则可循；(4)对噪声敏感；(5)只能在可以定义聚类的平均值的条件下才可以应用，即适合处理数值属性的数据； (6)采用欧式距离来测量样本间的亲疏程度，没有考虑变量间的相关性，因此算法对变量间的相关性极度敏感，在聚类分析前需要对变量进行相关性分析。

2. K-means聚类逻辑计算过程

第一步，指定聚类数目K。
在K-means聚类中，应首先给出需聚成多少类。聚类数目的确定本身并不简单，既要考虑最终的聚类效果，也要根据研究问题的实际需要。聚类数目太大或太小都将失去聚类的意义。

第二步，确定K个初始类中心。
类中心是各类特征的典型代表，指定聚类数目K后，还应指定K个类的初始类中心点。初始类中心点指定的合理性，将直接影响聚类收敛的速度。常用的初始类中心点的指定方法为经验选择法、随机选择法、最大最小法、最大距离法、Huffman树法（后面详细介绍）。

第三步，根据最近原则进行聚类。
依次计算每个数据点到K个类中心点的欧式距离，并按照距K个中心点距离最近的原则，将所有样本划分到最近的类中，形成K个类。其中欧式距离为

第四步，重新确定K个类中心。
中心点的确定原则是，依次计算各类中所有数据点变量的均值，并以均值点作为K个类中心，其计算公式为

第五步，聚类终止。
判断是否已经满足终止聚类的条件，如果没有满足则返回到第三步，不断反复上述过程，直到满足迭代终止条件。聚类终止的条件：

1. 迭代次数。当目前迭代次数等于指定的迭代次数时终止聚类；
2. 目标函数收敛。其中目标函数为
   
   即各样本到其所在类中心点的离差平方和小于某个指定值，即目标函数收敛，聚类终止。

3. K-means聚类初始中心点确定方法

由于K-均值算法初始中心点选取的随机性，可能出现选取的聚类种子过于邻近的情况，而导致聚类结果效果不好，也易陷入局部极小点。即初始类中心点指定的合理性，将直接影响聚类收敛的速度和效果。下面详细介绍确定初始聚类中心点的三种方法：最大距离法、最大最小法、Huffman树法。

（i）最大距离法

最大距离法是模式识别领域中一种基于试探的算法，思想是取尽可能离得远的对象作为聚类中心，提高了划分初始数据集的效率。最大距离法具体步骤为：
设$n$个数据对象，其中每个数据对象为$d$维，将$n$个数据对象聚成$k$类。
（1）有n 个样本$S_n=x_1,x_2,\cdots ,x_n$ ，计算每两点间的欧式距离，选取距离最大的两点$p,q$， $d_{pq}=\max \left\{d_{ij},i,j\in 1,2,\cdots ,n\right\}$，记$x_1^{\ast }=p,x_2^{\ast }=q,d_1^{\ast }=d_{pq}$ ；

（2）将数据$S_n$中剩余的 $n-2$个样本，以$x_1^{\ast }$ 和 $x_2^{\ast }$ 为中心进行聚类，若$d_{i1}<d_{i2},$$\forall i\in \left\{1,2,3,\cdots ,n/p,q\right\}$，则将$x_i$归于$x_1^{\ast }$，否则归于$x_2^{\ast }$，这样将$S_n$以$x_1^{\ast }$和$x_2^{\ast }$为中心分为两类；

（3）在已经聚成的$c$个类中找出每个类中离中心点最远的点，这样就得到$c$个点，在这$c$个点中每次取一个点，与已经得到的$c$个类的中心点组合成$c+1$个点，把$S_n$聚成$c+1$个类，这样我们得到了$S_n$的$c$个不同划分，并分别计算$c$个划分的准则函数，准则函数最小的那个划分为最优划分，并将形成最优划分的那个点作为第$c+1$个中心点。
准则函数：$\sum _{i=1}^k\sum _{x\in C_i}dist{\left(C_i,x_i\right)}^2$，对象到其簇质心的距离平方和；

（4）重复（3），直到找到$k$ 个聚类中心为止。

下面结合具体实例来详细说明最大距离算法来选取初始中心点的过程。
共有15个数据对象$\left(x_1,x_2,\cdots ,x_{15}\right)$，$\{\left(5,6\right);\left(6,6\right);\left(5,5\right);\left(2,4\right);\left(3,4\right);\left(2,3\right);\left(1,2\right);\left(1,1\right);$
$\left(2,2\right);\left(5,1\right);\left(5,2\right);\left(6,3\right);\left(6,2\right);\left(6,1\right);\left(6,0\right)\}$，要将这15个点聚成3个类，具体步骤如下：

• 根据欧式距离求得$\left(x_1,x_2,\cdots ,x_{15}\right)$每两点间的距离，找出距离最远的两点$x_2\left(6,6\right)$，$x_8\left(1,1\right)$，$d_{28}=7.07$，令$x_1^{\ast }=x_2$，$x_2^{\ast }=x_8$；
  
• 以$x_2$，$x_8$为聚类中心，依次比较$x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10},x_{11},x_{12},x_{13},x_{14},x_{15}$到$x_2,x_8$的欧式距离$d_{i2},d_{i8}$，若$d_{i2}<d_{i8}$则归为$x_1^{\ast }$，否则归为$x_2^{\ast }$，最终将数据聚成两类，$S_{21}^{\ast }=\left\{x_1,x_2,x_3,x_{12},x_{11},x_{13},x_{14}\right\}$，$S_{22}^{\ast }=\left\{x_4,x_5,x_6,x_7,x_8,x_9,x_{10},x_{15}\right\}$；
• $S_{21}^{\ast }$中距离中心点$x_2$最远的点为$x_{14}$，$S_{22}^{\ast }$中离中心点$x_8$最远的点为$x_{15}$；
• 分别用$\left\{x_2,x_8,x_{14}\right\}$和$\left\{x_2,x_8,x_{15}\right\}$把15个对象聚成3类，并分别计算得到$\left\{x_2,x_8,x_{14}\right\}$和$\left\{x_2,x_8,x_{15}\right\}$聚类结果的准则函数值分别为43和55， 可知以$\left\{x_2,x_8,x_{14}\right\}$为中心点得到的聚类结果更优。
  

（ii）最大最小距离法
最大最小距离算法的基本思想是取尽可能离得远的对象作为初始聚类中心，得到对数据集较好的初始划分，目的是避免K-means聚类算法初值选取的聚类中心过于邻近，多个聚类中心都被选择在同一个类中。最大最小距离法的具体步骤为：

设数据集为$S=\left\{X_1,X_2,X_3,\cdots ,X_n\right\}$，初始聚类中心集为$V=\left\{V_1,V_2,\cdots ,V_m\right\}$，对象间的相异度是基于欧式距离度量的。
（1） 从数据集$S$中任意选取一个数据对象，将其作为第一个聚类中心点$v_1$，并将其放入$V$中；

（2） 计算$v_1$和数据集$S$中剩余的所有数据对象之间的距离，把距离最远的数据对象放入$V$中，将其作为第二个聚类中心点$v_2$；

（3） 计算数据集$S$中剩余的所有数据对象$X_i$，分别计算到$v_1$和$v_2$的距离$d_{i1}$和$d_{i2}$，选择其中较小的距离$min\left(d_{i1},d_{i2}\right)$，即找到剩余每个对象到已有聚类中心最近的距离；

（4） 计算$min\left(d_{i1},d_{i2}\right)$的最大值，即$\max \left(min\left(d_{i1},d_{i2}\right)\right)$，与其对应的数据$X_i$即为第三个聚类中心$v_3$；

（5） 假设已找到$r\left(r<k\right)$个聚类中心$\left\{v_i,i=1,2,\cdots ,r\right\}$，现在确定第$r+1$个聚类中心，$\max \left\{\min \left(d_{i1},d_{i2},\cdots ,d_{ir}\right)\right\},i=1,2,\cdots ,N$所对应的数据$X_i$即为第$r+1$个聚类中心；

（6） 重复第（5）步，直到$r+1=k$为止。
说明：（1）~（2）步可以用最大距离法中的第（1）步进行简化，选取距离最远的两个对象。

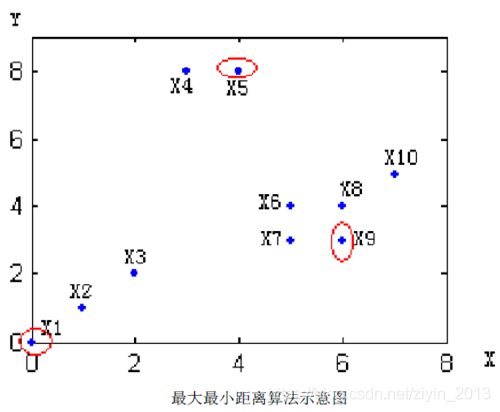
下面给出一个具体实例来详细说明最大距离算法的过程，
共有10个点$\left(x_1,x_2,\cdots ,x_{10}\right)$，具体步骤如下：

• 任选一个点作为第一个聚类中心，$v_1=x_1$，坐标为$\left(0,0\right)$；
• 在剩余点中计算到$v_1$距离最大的点作为第二个类的聚类中心，$v_2=x_5$；
• 计算剩余点到$v_1$、$v_2$的最小距离；
  $x_2$：$\min \left(\left|x_2-v_1\right|,\left|x_2-v_2\right|\right)=\left|x_2-v_1\right|$
  $x_3$：$\min \left(\left|x_3-v_1\right|,\left|x_3-v_2\right|\right)=\left|x_3-v_1\right|$
  $x_4$：$\min \left(\left|x_4-v_1\right|,\left|x_4-v_2\right|\right)=\left|x_4-v_2\right|$
  $x_6$：$\min \left(\left|x_6-v_1\right|,\left|x_6-v_2\right|\right)=\left|x_6-v_2\right|$
  $x_7$：$\min \left(\left|x_7-v_1\right|,\left|x_7-v_2\right|\right)=\left|x_7-v_2\right|$
  $x_8$：$\min \left(\left|x_8-v_1\right|,\left|x_8-v_2\right|\right)=\left|x_8-v_2\right|$
  $x_9$：$\min \left(\left|x_9-v_1\right|,\left|x_9-v_2\right|\right)=\left|x_9-v_2\right|$
  $x_{10}$：$\min \left(\left|x_{10}-v_1\right|,\left|x_{10}-v_2\right|\right)=\left|x_{10}-v_2\right|$
• 计算
  $\max \left(\left|x_2-v_1\right|,\left|x_3-v_1\right|,\left|x_4-v_2\right|,\left|x_6-v_2\right|,\left|x_7-v_2\right|,\left|x_8-v_2\right|,\left|x_9-v_2\right|,\left|x_{10}-v_2\right|\right)=\left|x_9-v_2\right|$
  因此，第三个初始聚类中心的候选对象为$x_9$，坐标$\left(6,3\right)$；
  

（iii）Huffman树
Huffman树简单的说就是带权路径长度之和最小的二叉树也称最优二叉树。给定n个数据点的权值，构造Huffman树的算法描述如下：
（1） 根据n个给定的权值$\left\{w_1,w_2,\cdots ,w_n\right\}$，构成n棵二叉树的集合$F=\left\{T_1,T_2,\cdots ,T_n\right\}$，每棵二叉树$T_i$只有根节点；

（2） 在$F$中选两棵根节点权值最小的树作为左右子树，构造一棵二叉树，新的二叉树根节点的权值等于其左右子树根节点权值之和；

（3） 在$F$中删除这两棵子树，同时将新得到的二叉树加入$F$中；

（4） 重复（2）和（3），直到$F$中只剩一棵树为止。

基于Huffman树思想确实K-均值聚类的初始聚类中心具体步骤如下：
（1） 根据Huffman树的思想，采用欧式距离计算各数据点之间的相异度，对于构造树时，采用左右结点的算术平均值作为新的二叉树根结点的值（也可以采用左右子树根节点权值之和作为新的二叉树根结点）；

（2） 对于构造出来的Huffman树，按构造结点的逆序找到$k-1$个结点，根据图论理论克制，去掉这$k-1$个结点可将该树分为$k$个子树，这$k$个子树的平均值即初始的$k$个聚类中心。

下面举例说明构造树并得到初始中心的过程。假设有一组一维数据集$\left(x_1,x_2,\cdots ,x_6\right)$，它们对应的权值为$\left(12,34,56,78,8,98\right)$，需要将这六个点聚成3类，具体过程如下：

• 首先根据欧式距离计算6个对象之间的相异度，得到相异度矩阵；
• 找到矩阵中最小值即4，也就是数据点$x_1\left(12\right),x_5\left(8\right)$的相异度，计算这两个点的算术平均值为$x_{11}=\frac{x_1+x_5}{2}=10$，并作为$x_1,x_5$的中间节点加入树。在数据集中删掉$x_1,x_5$，并将$x_{11}$加入到数据集得到新的数据集$\left(x_{11},x_2,x_3,x_4,x_6\right)$对应的权值为$\left(10,34,56,78,98\right)$，计算它们的相异度矩阵；
  
• 重复第（2）步直到数据集中只剩下一个对象，剩下的迭代过程相异度矩阵变化如下。
  
• 将数据集聚成3类，即$k=3$在已构造的树中按节点构造的逆序找出$k-1$个点，即57.75和27.5，去掉这两点即可将构造树分为3个子树$\left(x_1,x_5\right)\left(x_2,x_3\right)\left(x_4,x_6\right)$对应树中$\left(8,12\right)\left(34,56\right)\left(78,98\right)$。三个子树的平均值10,45,88即为3个簇的初始中心点。
  

4. K-means聚类应用示例

为研究不同地区的经济发展特点，根据各地区GDP、GDP指数、人均GDP指标数据，将北京市、天津市、江苏省等10个地区按照其经济水平分成3类。

• 对数据进行标准化，消除因指标量纲不同对聚类结果的影响。采用正向极差化法，公式如下：
  
  
• 采用欧式距离，计算样本间亲疏程度；
  两个样本之间的欧氏距离是样本各个变量值之差的平方和的平方根，计算公式为
  
  其中样本$x=(x_1,x_2,...,x_n)，y=(y_1,y_2,...,y_n)$ 。使用前一般需要将数据标准化，距离越大，差异度越大。
• 分别运用最大距离法、HUFFMAN树、最大最小距离法确定初始聚类中心；不同的方法得到的初始聚类中心不同。
  
• 运用SPSS，将上述初始聚类中心依次导入，分别进行聚类；
  

初始聚类中心的选择会对聚类结果产生一定影响。运用最大距离法、最大最小距离法确定初始聚类中心虽然不同，但是最终的聚类结果却是一样的；运用HUFFMAN树得到的初始聚类中心与其他两种方法不同，最终的聚类结果也有所差异。

总结
K-Means是聚类算法中最常用的一种，算法最大的特点是简单，好理解，运算速度快。但是，只能应用于连续型的数据；并且初始聚类中心选择的好与坏将会对聚类结果的质量产生很大影响；另外，对于聚类数K值的选择还没有很好的准则可循。所以，在实际应用中，要多次调整聚类数K值、初始聚类中心点等参数，结合自己的业务知识选择一个较优的结果。

ps：初衷是通过撰写博文记录自己所学所用，实现知识的梳理与积累；将其分享，希望能够帮到面临同样困惑的小伙伴儿。如发现博文中存在问题，欢迎随时交流~~