深度优先搜索及奇偶剪枝
深度优先搜索实现方式有很多种,我学习的是借助于递归来完成的,先讲一个简单的例子:给定一个整数 n,输出n的全排列;
先用深搜实现一下:
#include
int book[100] ,a[100],sum = 0; 用a数组来储存n的排列,用book数组记录a数组中有哪些元素
void dfs(int n,int step){
int i;
if (step==n){ //这是判断打印的条件 即 当数组内的元素达到n时结束
sum++; //用来记录排列的个数
for (i=0;i 看了代码是不是对深搜有所了解了? 深搜就是按定一种方式一只运行下去,直到满足某种特定条件或者走不下去时回溯,按另一条路继续运行。
看代码看累了?给你讲个故事放松一下:
话说有一条可爱的狗狗,一天它去散步,走进了了一座神秘的宫殿,这座宫殿辉煌无比想一条迷宫一样,狗狗在里面发现了一块诱人不对..诱狗的骨头,它急忙跑过去,但当它捡起,,叼起来时,感觉宫殿摇晃起来,它能感觉到地面在下沉,狗狗明白了这是一个陷阱,它拼命的想要跑出这条迷宫。这个迷宫的出口离它有一定距离,并且门是关闭的,只有再那特定的一秒钟才开启,当小狗停留在地板上超过一秒是它就会掉下去,所以它必须再那特定的时刻恰好到达门口。已知它的位置和这条迷宫的布局和门开启的时间(s),它一秒只能移动一块地板的距离,并且有障碍物的阻拦,问它能不能逃出去?
故事听完要做题了,就是上面那道题,这道题是HDUOJ的problem-1010。
输入由多个测试用例组成。每个测试用例的第一行包含三个整数n、m和t(1<n,m<7;0<t<50),分别表示迷宫的大小(行数和列数)和门将打开的时间。接下来的N行给出迷宫布局,每行包含M个字符。字符是下列之一:
| 'X': 障碍物; |
输入以3个0未结束标志,此时测试样例不被处理。
可以逃出输出YES,不能逃出 输出 NO。
用深度优先搜索实现一下:
#include
#include
int book[8][8],map[8][8];//二维数组book标记该点是否走过,二维map来储存迷宫布局
int next[4][2] = {{-1,0},{1,0},{0,-1},{0,1}};//记录狗狗的下一步怎么走:上,下,左,右
int flag = 0;//标志狗狗是否逃出去了
void dfs(int x,int y,int n,int m,int nt,int t){//x和y记录狗狗的位置,n,m记录迷宫的大小,nt记录狗狗所处时间,t代表出口关闭时间
book[x][y] = 1;
int i,tx,ty;
if (nt==t&&map[x][y]=='D'){
flag = 1;
return ;
}
if (nt>t)
return ;
for (i=0;i<4;i++){
tx = x + next[i][0];
ty = y + next[i][1];
if (book[tx][ty]==1||tx<0||tx>=n||ty<0||ty>=m||map[tx][ty]=='X')
continue;
dfs(tx,ty,n,m,nt+1,t);
book[tx][ty] = 0;
if (flag==1)
return ;
}
}
int main (){
int n,m,t,i,j,x,y;
scanf("%d%d%d",&n,&m,&t);
while (!(n==0&&m==0&&t==0)){
flag = 0;
for(i=0;i 这样就结束了?一提交,发现超时了,原因是执行了太多次函数了,怎么办?接下来讲一下,深度优先搜索的奇偶剪枝。
奇偶剪枝:
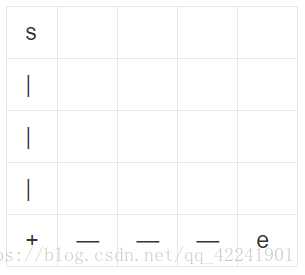
看上图假设s坐标(1,1),e坐标(5,5),那么s到e的最短路径为:(5-1) + (5-1) = 8 是个偶数。这里有个结论:那么从点s到点e无论怎么走,所走的步数肯定也是偶数。
那么如果规定了步数k看能否恰好到达,首先他得有个前提,那就是规定步数与起点到终点的最短路径d 奇偶性肯定是一样的。
所以我们上题中每走一步就可以提前判定它是不是在规定步数一定不能恰好到达。
闲话少说上代码(深度优先搜索+奇偶剪枝):
#include
#include
#include
#include
int book[8][8],map[8][8];
int next[4][2] = {{-1,0},{1,0},{0,-1},{0,1}};
int flag = 0;
int ex,ey;
void dfs(int x,int y,int n,int m,int nt,int t){
book[x][y] = 1;
int i,tx,ty;
if (nt==t&&map[x][y]=='D'){
flag = 1;
return ;
}
if (nt>t)
return ;
if (flag)
return ;
int tem=t-nt-abs(ex-x)-abs(ey-y);//这里就是奇偶剪枝的核心代码 t-nt 代表了剩余步数,abs(ex-x)+abs(ey-y)是当前位置到终点的最短路径;
if(tem<0||tem&1)//终止条件:剩余步数比最短路径少,剩余步数与最短路径奇偶性不同;
return;
for (i=0;i<4;i++){
tx = x + next[i][0];
ty = y + next[i][1];
if (book[tx][ty]==1||tx<0||tx>=n||ty<0||ty>=m||map[tx][ty]=='X')
continue;
dfs(tx,ty,n,m,nt+1,t);
book[tx][ty] = 0;
if (flag==1)
return ;
}
}
int main (){
int n,m,t,i,j,x,y;
scanf("%d%d%d",&n,&m,&t);
while (!(n==0&&m==0&&t==0)){
flag = 0;
for(i=0;i