python机器学习手写算法系列——优化器 Optimizers

本文用一个很简单的一元线性回归问题为例，实现了梯度下降(SGD), Momentum, Nesterov Accelerated Gradient, AdaGrad, RMSProp and Adam.

梯度下降

我们首先回顾一下梯度下降，以本系列第一篇文章《python机器学习手写算法系列——线性回归》为例。

目标函数：

$$y=f(\theta ,x)$$

线性回归目标函数为：

$$y=ax+b+\epsilon$$
$$\hat{y}=ax+b$$

损失函数为：

$$J(\theta )$$

线性回归损失函数为：

$$J(a,b)=\frac{1}{2n}\sum _{i=0}^n(y_i-{\hat{y}}_i{)}^2$$

优化函数：

$$\theta =\theta -\alpha \frac{\partial J}{\partial \theta }$$

对于一元线性回归的优化函数：

$$a=a-\alpha \frac{\partial J}{\partial a}$$
$$b=b-\alpha \frac{\partial J}{\partial b}$$

这里 $\frac{\partial J}{\partial a}$ 和 $\frac{\partial J}{\partial b}$ 分别是：

$$\frac{\partial J}{\partial a}=\frac{1}{n}\sum _{i=0}^{n}x({\hat{y}}_i-y_i)$$

$$\frac{\partial J}{\partial b}=\frac{1}{n}\sum _{i=0}^n({\hat{y}}_i-y_i)$$

这里$\hat{y}$是y的估计值，$\theta$是参数，$J$是损失函数，$\alpha$是学习率，下同。

这里用python实现的代码如下

def model(a, b, x):
    return a*x + b

def cost_function(a, b, x, y):
    n = 5
    return 0.5/n * (np.square(y-a*x-b)).sum()

def sgd(a,b,x,y):
    n = 5
    alpha = 1e-1
    y_hat = model(a,b,x)
    da = (1.0/n) * ((y_hat-y)*x).sum()
    db = (1.0/n) * ((y_hat-y).sum())
    a = a - alpha*da
    b = b - alpha*db
    return a, b

我们优化100次以后得到的结果如下：

这时的损失是0.00035532090622957674，我们这里把它记下来，之后，我们将分别用其他的优化函数达到这个值。看看他们需要多少次计算。

Momentum

Momentum，他和梯度下降相比，增了考虑了之前梯度，即更新参数的时候，除了梯度之外，也加上了之前的梯度（Momentum）。

$$m=\beta m-\alpha \frac{\partial J}{\partial \theta }$$

$$\theta =\theta +m$$

对于一元线性回归来说：

$$m_a=\beta m_a-\alpha \frac{\partial J}{\partial a}$$

$$a=a+m_a$$

$$m_b=\beta m_b-\alpha \frac{\partial J}{\partial b}$$

$$b=b+m_a$$

其中：

$$\frac{\partial J}{\partial a}=\frac{1}{n}\sum _{i=0}^{n}x({\hat{y}}_i-y_i)$$

$$\frac{\partial J}{\partial b}=\frac{1}{n}\sum _{i=0}^n({\hat{y}}_i-y_i)$$

Python实现

def momentum(a, b, ma, mb, x, y):
    n = 5
    alpha = 1e-1
    beta = 0.9
    y_hat = model(a,b,x)
    da = (1.0/n) * ((y_hat-y)*x).sum()
    db = (1.0/n) * ((y_hat-y).sum())
    ma = beta*ma - alpha*da
    mb = beta*mb - alpha*db
    a = a + ma
    b = b + mb
    return a, b, ma, mb

为了达到同样的损失，Momentum用了46次。只有梯度下降的一半不到。

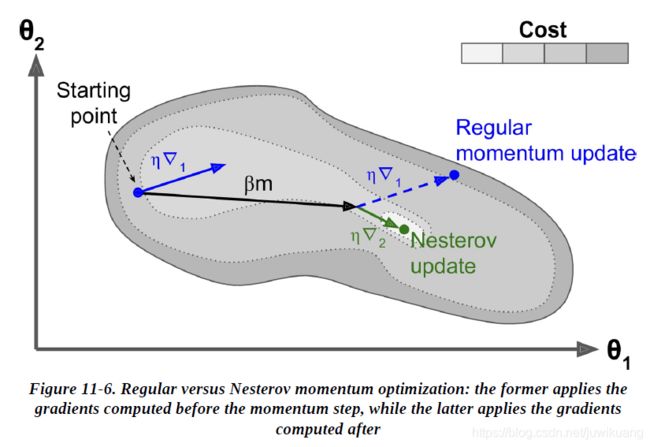
Nesterov Accelerated Gradient

Nesterov Accelerated Gradient（NAG），又叫Nesterov momentum optimization，是Yurii Nesterov在1983年提出的。相对于Momentum，它有一点“前瞻”。它在计算损失函数的时候，就已经把Momentum放进了参数里了。这样它计算的就是更新后损失的一阶导数。
$$m=\beta m-\alpha \frac{\partial J(\theta +\beta m)}{\partial \theta }$$

$$\theta =\theta +m$$

对于一元线性回归来说：

$$m_a=\beta m_a-\alpha \frac{\partial J(a+\beta m_a)}{\partial a}$$

$$a=a+m_a$$

$$m_b=\beta m_b-\alpha \frac{\partial J(b+\beta m_b)}{\partial b}$$

$$b=b+m_a$$

其中，

$$\frac{\partial J}{\partial a}=\frac{1}{n}\sum _{i=0}^{n}x({\hat{y}}_i-y_i)$$

$$\frac{\partial J}{\partial b}=\frac{1}{n}\sum _{i=0}^n({\hat{y}}_i-y_i)$$

这里，我们只需要令

$$\hat{y}=(a+m_a)x+(b+m_b)$$

即可。其他地方和Momentum一样。

Python实现

def nesterov(a, b, ma, mb, x, y):
    n = 5
    alpha = 1e-1
    beta = 0.9
    y_hat = model(a+ma,b+mb,x)
    da = (1.0/n) * ((y_hat-y)*x).sum()
    db = (1.0/n) * ((y_hat-y).sum())
    ma = beta*ma - alpha*da
    mb = beta*mb - alpha*db
    a = a + ma
    b = b + mb
    return a, b, ma, mb

这里，我们用了21次达到了同样的损失。

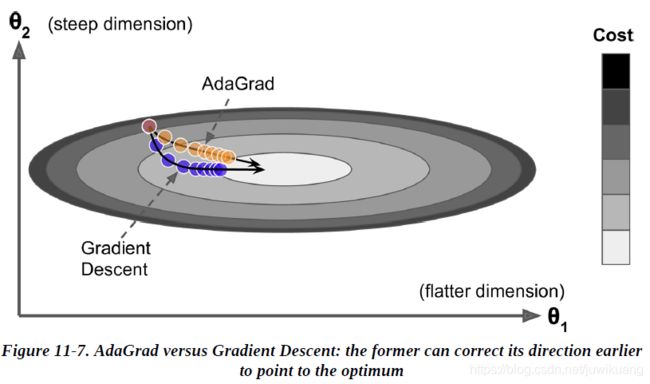
AdaGrad

在下图中，蓝色的为梯度下降，它朝着梯度最大的方向快速前进，而不是朝着全局最后前进。黄色的是AdaGrad，它指向的是全局最优。它的办法是缩小（scaling down）最大的梯度参数。

公式：

$$ϵ=1e-10$$

$$s=s+\frac{\partial J}{\partial \theta }\odot \frac{\partial J}{\partial \theta }$$

$$\theta =\theta -\alpha \frac{\partial J}{\partial \theta }\oslash \sqrt{s+ϵ}$$

同样，我们这里用a，b替换$\theta$ 即可。

Python代码：

def ada_grad(a,b,sa, sb, x,y):
    epsilon=1e-10
    n = 5
    alpha = 1e-1
    y_hat = model(a,b,x)
    da = (1.0/n) * ((y_hat-y)*x).sum()
    db = (1.0/n) * ((y_hat-y).sum())
    sa=sa+da*da + epsilon
    sb=sb+db*db + epsilon
    a = a - alpha*da / np.sqrt(sa)
    b = b - alpha*db / np.sqrt(sb)
    return a, b, sa, sb

这里，我们用了114次，比梯度下降还多了14次。

RMSProp

AdaGrad的风险是，它降速降的太快。所以反而花了更长的时候才达到全局最优。甚至可能永远无法达到全局最优。PMSProp降低了这种降速。方法就是乘以一个参数$\beta$，通常其值为0.9.

$$ϵ=1e-10$$

$$s=\beta s+(1-\beta )\frac{\partial J}{\partial \theta }\odot \frac{\partial J}{\partial \theta }$$

$$\theta =\theta -\alpha \frac{\partial J}{\partial \theta }\oslash \sqrt{s+ϵ}$$

Python代码

def rmsprop(a,b,sa, sb, x,y):
    epsilon=1e-10
    beta = 0.9
    n = 5
    alpha = 1e-1
    y_hat = model(a,b,x)
    da = (1.0/n) * ((y_hat-y)*x).sum()
    db = (1.0/n) * ((y_hat-y).sum())
    sa=beta*sa+(1-beta)*da*da + epsilon
    sb=beta*sb+(1-beta)*db*db + epsilon
    a = a - alpha*da / np.sqrt(sa)
    b = b - alpha*db / np.sqrt(sb)
    return a, b, sa, sb

这里，仅仅用了11次，就达到了梯度下降同样的损失。

Adam

我们最后介绍Adam，Adam就是adaptive moment estimation。他是momentum和RMSProp的结合。

$$m={\beta }_{1}m-(1-{\beta }_1)\frac{\partial J}{\partial \theta }$$

$$s={\beta }_{2}s+(1-{\beta }_2)\frac{\partial J}{\partial \theta }\odot \frac{\partial J}{\partial \theta }$$

$$\hat{m}=\frac{m}{1-{\beta }_1^T}$$

$$\hat{s}=\frac{s}{1-{\beta }_2^T}$$

$$\theta =\theta +\alpha \hat{m}\oslash \sqrt{\hat{s}+ϵ}$$

这里的$\odot$和$\oslash$是点乘和点除，或者叫element-wise product 和 element-wise division。

Python实现

def adam(a, b, ma, mb, sa, sb, t, x, y):
    epsilon=1e-10
    beta1 = 0.9
    beta2 = 0.9
    n = 5
    alpha = 1e-1
    y_hat = model(a,b,x)
    da = (1.0/n) * ((y_hat-y)*x).sum()
    db = (1.0/n) * ((y_hat-y).sum())
    ma = beta1 * ma - (1-beta1)*da
    mb = beta1 * mb - (1-beta1)*db
    sa = beta2 * sa + (1-beta2)*da*da
    sb = beta2 * sb + (1-beta2)*db*db
    ma_hat = ma/(1-beta1**t)
    mb_hat = mb/(1-beta1**t)
    sa_hat=sa/(1-beta2**t)
    sb_hat=sb/(1-beta2**t)
    
    a = a + alpha*ma_hat / np.sqrt(sa_hat)
    b = b + alpha*mb_hat / np.sqrt(sb_hat)
    
    return a, b, ma, mb, sa, sb

Adam用了25次。

Nadam

Nadam就是Nesterov + Adam。nadam和adam相比，仅仅差在计算损失的时候用$\theta +m$替换了$\theta$：

$$m={\beta }_{1}m-(1-{\beta }_1)\frac{\partial J(\theta +{\beta }_{1}m)}{\partial \theta }$$

$$s={\beta }_{2}s+(1-{\beta }_2)\frac{\partial J(\theta +{\beta }_{1}m)}{\partial \theta }\odot \frac{\partial J(\theta +{\beta }_{1}m)}{\partial \theta }$$

$$\hat{m}=\frac{m}{1-{\beta }_1^T}$$

$$\hat{s}=\frac{s}{1-{\beta }_2^T}$$

$$\theta =\theta +\alpha \hat{m}\oslash \sqrt{\hat{s}+ϵ}$$

def nadam(a, b, ma, mb, sa, sb, t, x, y):
    epsilon=1e-10
    beta1 = 0.9
    beta2 = 0.9
    n = 5
    alpha = 1e-1
    # to modify adam to nadam, 
    # we only modify here
    # with a = a + ma 
    # and b = b + mb
    y_hat = model(a+ma,b+mb,x)
    da = (1.0/n) * ((y_hat-y)*x).sum()
    db = (1.0/n) * ((y_hat-y).sum())
    ma = beta1 * ma - (1-beta1)*da
    mb = beta1 * mb - (1-beta1)*db
    sa = beta2 * sa + (1-beta2)*da*da
    sb = beta2 * sb + (1-beta2)*db*db
    ma_hat = ma/(1-beta1**t)
    mb_hat = mb/(1-beta1**t)
    sa_hat=sa/(1-beta2**t)
    sb_hat=sb/(1-beta2**t)
    
    a = a + alpha*ma_hat / np.sqrt(sa_hat)
    b = b + alpha*mb_hat / np.sqrt(sb_hat)
    
    return a, b, ma, mb, sa, sb

总结

针对我们的一元线性回归。达到同样的效果（损失），各种优化器所有迭代次数：

优化算法	迭代次数	冲量	Nesterov	adaptive 自调节	备注
SGD	100	❌	❌	❌	–
Momentum	46	✔️	❌	❌	–
Nesterov	21	✔️	✔️	❌	–
AdaGrad	114	❌	❌	✔️	–
RMSProp	11	❌	❌	✔️	–
Adam	25	✔️	❌	✔️	深度学习默认值
Nadam	14	✔️	✔️	✔️	–

注意，这里仅仅是我这个数据集的表现。本文不是介绍优化用法的文章。这里简单说说。AdaGrad（以及其变种RMSProp）, Adam, Nadam这些名字里面带ada(adaptive)的，都能起到缩小(decay)学习率的效果。但是如果他们的学习率缩小的太快，会使得他们反而变慢，反而需要很长时间才达到最优，甚至永远达不到。我用tensorflow的时候，一般先用adam，如果效果不好，就用Learning Rate Scheduling技术，得到合适的学习率。然后改成SGD。也可以用Gradient Clipping技术。具体的请参考大牛作品。

参考资料

写作本文的时候，正好再看《hands-on machine learning (2nd Edition)》，所以就拿了这本书做参考了，文中截图均来自这本书。

我从来没看过你们经常说的西瓜书，也没有计划看它。机器学习应该从英文资料入门，而不是中文。看英文前期吃力，后期就轻松了。看中文前期轻松，后面就吃力了。

动手写优化函数，你也可以

这些优化函数，实现的时候，直接套用书上的公式即可。我一共用了三个小时，实现了所有的函数。其中，函数弄错了浪费一小时。查找点乘和点除的latex或者markdown表示浪费了半小时。

点乘和点除的markdown / latex：

\odot
\oslash

我觉得优化函数是我做了这么多手写算法里面最简单的了。基本上不怎么需要推导公式，直接拿来用即可。

你可以试着自己写一下，实在写不出来的，可以参考一下我的代码。

祝你机器学习顺利。

May the machine learn with you.

Github代码地址

https://github.com/EricWebsmith/machine_learning_from_scrach

大陆用户渲染github jupyter notebook 请使用jupyter notebook viewer：
https://nbviewer.jupyter.org/github/EricWebsmith/machine_learning_from_scrach/blob/master/optimizers.ipynb

python机器学习手写算法系列

python机器学习手写算法系列——线性回归

python机器学习手写算法系列——逻辑回归

python机器学习手写算法系列——优化函数

python机器学习手写算法系列——决策树

python机器学习手写算法系列——kmeans聚类

python机器学习手写算法系列——GBDT梯度提升分类

python机器学习手写算法系列——GBDT梯度提升回归

python机器学习手写算法系列——贝叶斯优化 Bayesian Optimization

python机器学习手写算法系列——PageRank算法