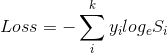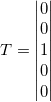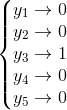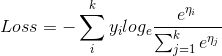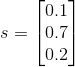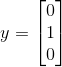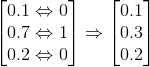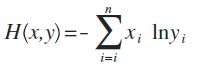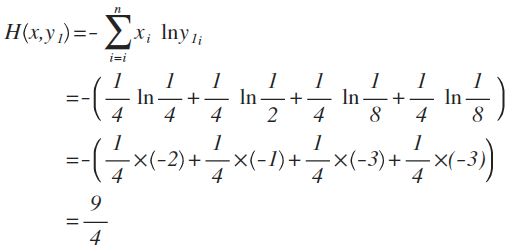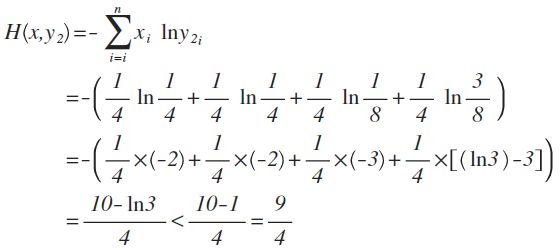BP神经网络中交叉熵作为损失函数的原理——softmax前世今生系列(4)

导读：

softmax的前世今生系列是作者在学习NLP神经网络时，以softmax层为何能对文本进行分类、预测等问题为入手点，顺藤摸瓜进行的一系列研究学习。其中包含：

1.softmax函数的正推原理，softmax的代数和几何意义，softmax为什么能用作分类预测，softmax链式求导的过程。

2.从数学的角度上研究了神经网络为什么能通过反向传播来训练网络的原理。

3.结合信息熵理论，对二元交叉熵为何适合作为损失函数进行了探讨。

通过对本系列的学习，你可以全面的了解softmax的来龙去脉。如果你尚不了解神经网络，通过本系列的学习，你也可以学到神经网络反向传播的基本原理。学完本系列，基本神经网络原理就算式入门了，毕竟神经网络基本的网络类型就那几种，很多变种，有一通百通的特点。

网上对softmax或是神经网络反向传播知识的整理，基本都通过一个长篇大论堆积出来，一套下来面面俱到但又都不精细。本文将每个环节拆开，分别进行详细介绍，即清晰易懂，又减轻了阅读负担，增加可读性。本文也借鉴了其他作者的内容，并列举引用，希望大家在学习过程中能有所收获

本章内容提要：

前三篇文章详细的介绍了softmax函数的概念和原理，softmax函数在神经网中扮演的角色，以及为什么softmax函数能解决分类问题。

分类问题一般来说属于数据的预测范畴，最初的预测往往和真实结果相差很远，而神经网络正是通过一遍遍的预测，一遍遍的评估预测结果，从而对整个网络模型进行修正，最终得到一个有效的分类模型。过程如下：

          

其中分类模型之前已经讲过了，本文就来讲一讲如何对神经网络的分类结果做评估，即如何判断分类的结果和真实的结果的差异。

一、损失函的概念

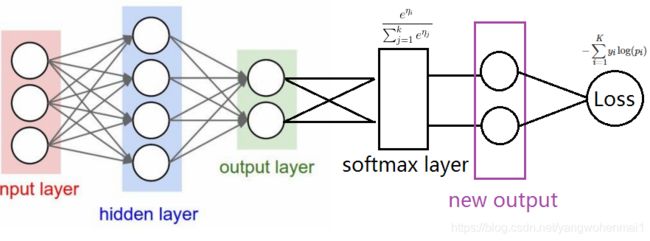
在预测模型中，评估神经网络预测结果的工具叫损失函数。损失指的就是预测值与真实值之间的差异，差异越小代表预测结果越接近真实值，损失函数在神经网络结构中的位置如下图：

                  

从图上可以看出，损失函数Loss的输入值，是经过softmax层计算得出的预测概率分布。

损失函数并不是一个具体的函数，他的形态多种多样，比如均方差，标准差，平均绝对误差等，在评估概率分布时，通常我们选择交叉熵作为损失函数。交叉熵公式为：

                                                                           

交叉熵是一个伟大的公式，提到交叉熵就引申出了信息熵的概念，网上有很多优秀的文章对此进行介绍。推导过程不再讲解，我们只利用其结论即可。参考资料：

https://www.cnblogs.com/liaohuiqiang/p/7673681.html

https://www.zhihu.com/question/22178202

 

二、交叉熵与神经网络的对应关系

首先我们来解释一下交叉熵的表达式意义：

                                                                            

这里我们要引入本系列教程中，第一篇文章中提到的分类模型：T向量

（参考链接：softmax函数的正推原理——softmax前世今生系列(1)）

                                                                                        

Loss函数中的i个y值，对应的就是T向量中的5个数字，对应关系为：

                                                                                      

此时对应的概率分布关系为：

                                                                                      

Loss函数中的S对应的是，经过softmax层计算后的概率分布，即：

                                                                                    

 因此交叉熵算法表达式为：

                                                                          

 

三、交叉熵作为损失函数的数学逻辑

我们假设有一个分类的预测结果为：

                                                                                       

其对应的真实分类结果为：

                                                                                        

预测结果看起来和真实结果很接近了，但是仍有差异，两者对应关系可以表示为：

                                                                               

左边的矩阵是预测值和真实值之间的对应关系，右边的矩阵就是预测值和真实值之间的差异。我们训练神经网络的目的就是使右侧差异矩阵中的数值越来越小。

计算一下y向量和s向量之间的交叉熵：

                                         

交叉熵代表这预测概率分布与真实概率分布之间的差异，所以差异越小越好，当差异为0时，预测值和真实值完全吻合。神经网络会根据这个原则，不断调整网络中的权重参数，使得计算出的交叉熵慢慢趋向于零。

根据对数函数定义知：

                                                                                       

因此，当预测结果s中的0.7趋向于1时，交叉熵趋向于0。由于s的所有概率之和为1，所以他项则趋向于0，此时预测结果s趋向于y，即：

                                                                   

以上就是神经网络中，交叉熵作为损失函数，评估预测结果的数学逻辑。

 

四、另一个计算方法例子

再贴网上一个的参考例子，巩固一下： 

                                                                       

这是公式定义，x、y都是表示概率分布（注：也有很多文章喜欢用p、q来表示），这个东西能干嘛呢？

假设x是正确的概率分布，而y是我们预测出来的概率分布，这个公式算出来的结果，表示y与正确答案x之间的错误程度（即：y错得有多离谱），结果值越小，表示y越准确，与x越接近。

比如：

x的概率分布为：{1/4 ，1/4，1/4，1/4}，现在我们通过机器学习，预测出来二组值：

y1的概率分布为  {1/4 ,  1/2 , 1/8 , 1/8}

y2的概率分布为  {1/4 ,  1/4 , 1/8 , 3/8}

从直觉上看，y2分布中，前2项都100%预测对了，而y1只有第1项100%对，所以y2感觉更准确，看看公式算下来，是不是符合直觉：

                                                     

 

                                                    

对比结果，H(x,y1)算出来的值为9/4，而H(x,y2)的值略小于9/4，根据刚才的解释，交叉熵越小，表示这二个分布越接近，所以机器学习中，经常拿交叉熵来做为损失函数(loss function)。 

五、总结

本文中我们学了一个新概念——损失函数。损失函数在神经网络中能对输出结果的准确性进行评判。神经网络根据损失函数的评判结果来修正网络模型。文中以交叉熵为例，演算了损失函数的计算过程。

下面问题来了，得到预测值和真实值之间的差异后，如何去修正我们的神经网络模型呢？那就是对神经网络求导了，也叫神经的反向传播。也是BP神经网络中BP的精髓所在。

可是为什么求导就能优化神经网络模型？我们究竟是对谁求导？对输出层求导？对隐藏层求导？对权重矩阵求导？甚至对softmax层求导？不同网络层之间的导数怎么传递？求导过程是什么样？

下篇文章我们一一道来。

传送门：神经网络正向传播及反向传播原理分析——softmax前世今生系列(5)

 

六、附学习笔记如下：

参考资料：

http://www.pianshen.com/article/8056145047/

https://segmentfault.com/a/1190000017320763?utm_source=tag-newest

https://www.cnblogs.com/lliuye/p/9549881.html

https://www.cnblogs.com/yjmyzz/p/7822990.html

交叉熵求导过程: https://blog.csdn.net/qian99/article/details/78046329