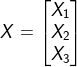神经网络正向传播及反向传播原理分析——softmax前世今生系列(5)
导读:
softmax的前世今生系列是作者在学习NLP神经网络时,以softmax层为何能对文本进行分类、预测等问题为入手点,顺藤摸瓜进行的一系列研究学习。其中包含:
1.softmax函数的正推原理,softmax的代数和几何意义,softmax为什么能用作分类预测,softmax链式求导的过程。
2.从数学的角度上研究了神经网络为什么能通过反向传播来训练网络的原理。
3.结合信息熵理论,对二元交叉熵为何适合作为损失函数进行了探讨。
通过对本系列的学习,你可以全面的了解softmax的来龙去脉。如果你尚不了解神经网络,通过本系列的学习,你也可以学到神经网络反向传播的基本原理。学完本系列,基本神经网络原理就算式入门了,毕竟神经网络基本的网络类型就那几种,很多变种,有一通百通的特点。
网上对softmax或是神经网络反向传播知识的整理,基本都通过一个长篇大论堆积出来,一套下来面面俱到但又都不精细。本文将每个环节拆开,分别进行详细介绍,即清晰易懂,又减轻了阅读负担,增加可读性。本文也借鉴了其他作者的内容,并列举引用,希望大家在学习过程中能有所收获
本章内容提要:
通过前四篇文章的学习,此时我们的知识体系里有了神经网络,分类函数,损失函数这三个重要模块。
掌握了数据从:输入→输出→预测分类→评估预测结果与真实结果差异;的原理以及推导过程。本文接着探讨在通过损失函数得到预测结果的误差后,下一步我们要怎么做,以及为什么要这么做。
得到损失函数计算出的损失值后,我们就要将损失值反响传播到网络中,网络会根据回传的损失值,修改网络模型参数,而后用修改后的网络模型对数据进行重新计算。修改网络模型的方法就是众所周知的求导(链式求导)了。这也是BP神经网络中back propagation的精髓了。在学习手动推导求导过程之前,我们先了解一下反响传播的本质,以及求导的目的。
一、神经网络反向传播示意图
拿出我们的经典图,图中新增了一些东西,图中红色的箭头表示神经网络反向传播的路线,网络部分多了两个黄色的区域,代表链接网络中层与层之间的权重矩阵,这也是后续要重点讨论的对象。
从图中可以看出,在损失函数Loss部分产生的损失值,随着网络正向传播来的方向,将误差值反向传播了回去。
 神经网络反向传播示意图
神经网络反向传播示意图
二、神经网络正向传播原理
下面是一个神经网的络构造图,此图便于我们对神经网络正向传播流程进行分析:
 神经网络内部结构图
神经网络内部结构图
首先,我们要搞清楚一个问题,求导是对谁求导。先回顾一下输入神经网络的输入X是怎么一步步传递到损失函数Loss的。输入层X到Loss要经过一下三个步骤:
第一步:输入层X与权重矩阵W相乘,得到输出z
第二步:输出z通过softmax函数转换成概率分布s
第三步:通过损失函数Loss,计算预测概率分布s和真实概率分布y之间的损失值loss
现在神经网络的原理是不是就很清楚了:
1.输入X为已知数据。
2.s是通过softmax函数计算而来,softmax函数为已知表达式
3.loss是通过交叉熵函数和真实的概率分布计算而来,交叉熵函数表达式已知,真实的概率分布已知。
4.矩阵W是未知数据
三、寻找求导目标及链式求导的应用
通过第二节的结论,显然,整个过程中只有一个未知量即W。
事实上我们所谓的训练神经网络最后的结果就是生成一个或多个参数矩阵W,所以我们反向传播损失值本质上也就是为了修改权重矩阵W。那么W就是我们要求导的终极目标,即:
![]()
但在损失函数和权重矩阵W之间,除损失函数以外,还间隔的有softmax层,以及输出层。那么我们就要以softmax层和输出层为桥梁,来对权重矩阵W求导,即所谓的链式求导:
因此,想求得权重矩阵的倒数,首先要求得损失函数与softmax层之间的倒数,再求softmax层与输出层z之间的导数,最后求得输出层与权重矩阵之间的导数。
原理流程图如下:
 反向传播示意图
反向传播示意图
四、总结
我们理清楚了神经网络的正向传播原理,恭喜你,可以说此时你已经从0到1的理解了神经网络原理,同时也明白了反向传播要求导的对象是谁,下一章就一起来手动推导神经网络反向传播公式吧~
传送门:手动推导softmax神经网络反向传播求导过程——softmax前世今生系列(6)