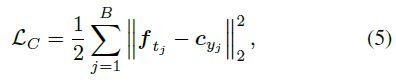Bag of Tricks and A Strong Baseline for Deep Person Re-identification

 

摘要

本文意在研究一个简单有效的行人重识别（ReID）baseline。近些年来基于深度学习的ReID取得了不错的进展，取得高光的表现。然而许多state-of-art的方式都是通过复杂的网络结构与多分枝特征拼接实现的。文献中有些高效的训练技巧简略的出现在一些论文或者源码中。本文将手机并且评估这些行人重识别的高效训练技巧。将这些技巧组合在一起，仅仅使用全局特征就可以在Market1501上达到85.9%的mAP。源码与模型可在github上找到。

 

背景

近些年来基于深度学习的ReID取得了不错的进展，取得高光的表现。然而许多state-of-art的方式都是通过复杂的网络结构与多分枝特征拼接实现的。文献中有些高效的训练技巧简略的出现在一些论文或者源码中。本文会收集并且评估这些ReID的训练技巧。使用所有训练技巧，ResNet50网络可以在Market1501上达到top1：94.5%，top5：85.9%的mAP。值得一提的是我们是用全局特征取得这样令人吃惊的表现的。

作为对比我们对去年ECCV2018与CVPR2018上发表的论文进行了综述。如图1所示，之前大多数工作都是在比较弱的baseline上进行扩展。在Market1501上23个baseline中只有2个超过了top1：90%的准确率。有4个baseline的top1准确率低于80%。在DukeMTMC-reID上所有baseline的rank-1都没有超过80%并且mAP不超过65%。我们认为强大的baseline对于推进研究的进展十分重要，因此我们对标准的baseline使用一些训练技巧得到了强baseline。我们的强baseline的源码已经开源出来了。

此外我们还发现有些文章与state-of-arts方法的比较并不公平。特别是改进的方式并不是方法本身，而是训练的技巧。但是训练技巧在文章中却轻描淡写的带过，让读者很容易错过这些信息。这会夸张了论文中方法的重要性。我们建议reviewers在审阅这些学术论文的时候也要将训练技巧考虑进去。

出去之前提到的原因，还有一个考虑是工业界更喜欢简单有效的模型，而不是在前向阶段将许多局部特征拼接在一起的方式。为了追求高精度，学术界经常结合多种局部特征或者利用语义信息进行姿态估计或者分割模型。大特征同样极大的降低了检索的速度。因此，我们希望使用一些技巧来改进ReID模型的能力，仅仅使用全局特征来得到好的表现。本文的目标总结如下：

1. 我们对许多发布在顶会的论文做了综述，发现他们大多数是建立在较差的baseline上的。
2. 对于学术界我们希望提供一个强baseline给研究人员作为取得更高行人ReId准确率的基础。
3. 对于社区来说，我们希望给reviewers一些参考，来判断哪些技巧会影响ReID模型的表现。我们建议在对比不同方式的效果的时候，reviewers也需要将这些技巧纳入考虑范围。
4. 对于工业界来说，我们希望提供一些有效的技巧从而在不消耗太多计算量的前提下获得更好的模型。

图1：在Market1501与DukeMTMC-reID数据集上不同baseline的表现。我们将自己的baseline与CVPR2018和ECCV2018上的baseline做了对比。

幸运的是，许多有效的训练技巧都呈现在一些论文或者开源项目中了。我们收集了许多技巧，并且在ReID数据集上对他们的效果进行了评估。经过许多试验，我们选择了六个技巧在本文进行介绍。有些方法是我们设计或者进行了一定改进的。我们将这些技巧应用到广为使用的baseline得到我们改进的baseline，在Market1501数据集上达到了94.5%与85.9%的mAP。此外，我们发现不同的论文选择不同的样本大小与batchsize大小，作为补充，我们也研究了这些因素对模型效果的影响。总结来说，本文的贡献总结如下：

1. 我们收集了一些在行人ReID领域有效的训练技巧。在这个基础上我们设计了一个新的瓶颈结构命名为BNNeck。此外，我们在两个应用广泛的数据集上评估每个技巧的改进。
2. 我们提供了一个强ReIDbaseline，在Market1501上达到了94.5%与85.9%的准确率。值得一提的是这个结果是利用ResNet50结构通过全局特征获得的。据我们所知，这是全局特征在行人ReID领域得到的最佳的表现。
3. 作为补充，我们评估输入样本尺寸与batchsize大小对ReID模型效果的影响。

 

标准Baseline

我们使用广泛使用的开源项目作为我们标准的baseline。标准baseline的backbone是ResNet50。训练阶段，pipline包括以下步骤：

1. 我们使用ImageNet下训练的参数来初始化ResNet50，将全连接参数改为N。N表示训练数据集中目标的个数。
2. 我们随机抽取P个对象，每个对象K张图来构成训练batch。最终的Batchsize为B=P×K。本文中，我们设置P=16，K=4。
3. 将每张样本resize成256×128像素大小，并pad10个像素0。随机crop成256×128矩形样本。
4. 样本以0.5的概率进行随机翻转。
5. 样本为值域范围为【0,1】之间的32位浮点数。RGB通道减去均值0.485,0.456,0.406，并分别处以0.229,0.224,0.225。
6. 模型输出ReID特征f与ID预测值logp。
7. ReID特征f用于计算triplet loss。ID预测值log p用于计算交叉熵损失函数。Triplet loss的权重设置为0.3。
8. Adam用于进行模型优化。初始化学习权重设置为0.00035并分别在第40次与70次epoch时下降0.1。整体训练120个epochs。

训练技巧

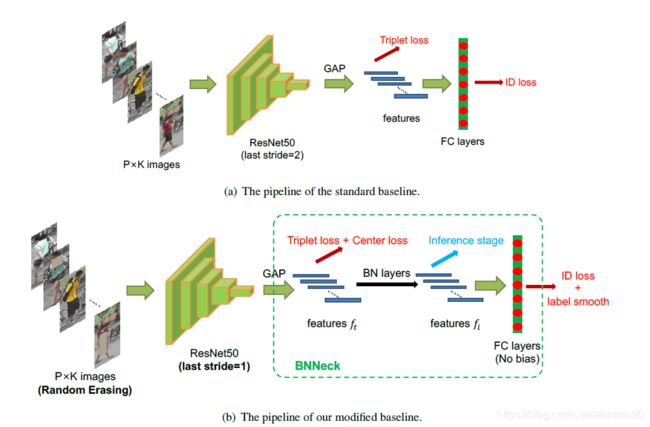
本章会介绍一些有效的行人ReID的训练技巧。大多数这样的训练技巧可以在不修改模型结构的前提下对标准baseline进行扩展。图2展示了本章使用的训练策略与模型结构。

 

图2 标准baseline与我们优化的baseline。

3.1 Warmup Learning Rate

学习率对ReID模型的表现会产生很大的影响。标准baseline是有一个大的常量学习率训练出来的。在【2】中warmup策略应用来增加网络的效果。如图3所示，在10epochs内线性的从3.5×10-5到3.5×10-4。此后，学习率分别在40epochs时下降到3.5×10-5，在70epochs时下降到3.5×10-6。学习率lr(t)在第7个epochs时计算如下：

3.2 随机擦除数据扩展（Random Erasing Augmentation）

在行人ReID中，图片中的行人有时会被其他物体遮挡。为了解决遮挡问题，提升ReID模型的鲁棒性，文献【27】提出了一种称为随机擦除数据扩展（Random Erasing Augmentation）的数据扩展方法。对于miniBatch中的一张图，Random Erasing的概率为pe,保持原样的概率为1-pe。REA在图片I中随机选择一个矩形区域Ie，大小为（We，He），将矩形的值随机抹去。假设图片I为S=W×H，区域为S=We×He，，我们将抹去区域表示为re = s/se。为了得到独一无二的区域，REA随机初始化一个点，如果且，那么我们将区域设置为选择的矩形区域。我们会持续迭代以上过程，直到选到理想的。选择出的擦除区域中每个像素分别设置为图像I的均值。

在本研究中，我们设置超参分别为。图4展示了其中一些例子。

3.3 标签平滑（Label Smoothing）

ID Embedding（IDE）【25】网络时行人重识别的一个基础baseline。IDE最后一层输出的是每张样本的ID预测值，是一个隐藏参数等于人的个数N的全连接层。一张样本，我们假设y为真实的ID标签，是第i类的预测概率。交叉熵损失函数计算如下：

由于分类的类别由人的ID决定，我们将这样的loss在本文中称为ID loss。

然而，行人重识别可以当做单步学习任务，因为测试集中的ID不会出现在训练集中。所以防止ReID模型过拟合训练数据中的ID就显得十分重要。Label smoothing(LS)在文献【17】中被提出，广泛应用在防止分类任务过拟合上。将表示如下：

这里是一个小常量，来降低模型在训练集上的置信度。本研究中，设置为0.1。当训练集非常大的时候，LS可以很大程度的改善模型的表现。

3.4 Last Stride

高分辨率总是可以丰富特征的粒度。文献【16】中，坐着溢出了backbone网络中最后一层降采样操作从而提升了featuremap的尺寸。为了方便表达，我们将骨干网络中的最后一个降采样操作表示为Last Stride。ResNet50中的Last Stride为2。当输入一张256×128的样本，ResNet50骨干网络输出的特征图尺寸大小为8×4。如果将last stride从2改为1，我们可以得到尺寸为（16×8）空间大小的特征图。这种操作仅仅增加了微小的计算量，并且没有引入更多的需要训练的参数。然而，高的空间分辨率带来了明显的改善。

3.5 BNNeck

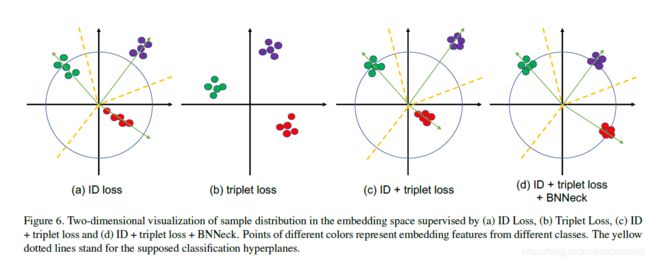
大多数ReID模型的训练会融合ID loss与triplet loss。如图5（a）中所示，标准的baseline中ID loss与triplet loss同时限制特征f。然而这两个loss从嵌入空间（Embedding Space）来说并不连续。

如图6（a）所示，ID loss构建了几个超平面来讲embedding space划分到不同子空间中。每一类的特征分布在不同的子空间中。本例前向运算中cosine距离会比欧式距离更加适用与ID loss优化的模型。另一方面，如图6（b）所示，triplet loss增强了类内的关系，类间的区分度在欧式空间更加分离。由于triplet loss不能提供全局优化约束，类内的距离有时候比类间的距离要小。广泛应用的方式是将ID loss与triplet loss组合在一起来训练模型。这种方式使得模型学习到更多的有区分度的特征。然而，对于embedding space中的杨比对来说，ID loss主要优化cosine距离，而triplet loss更加关注欧式距离。如果我们同时使用两个loss同时优化特征向量，他们的目标可能不一致。在训练过程中可能出现一个loss降低了另外一个loss一直在震荡或者甚至增加了的现象。

为了克服前面提到的问题，我们设计了一个如图5（b）所示的网络称为BNNeck。BNNeck仅仅在特征层后或者FC分类层后增加了一个BN层。BN层前的特征层表示为。我们使得通过BN层来得到正则化后的特征。在训练阶段，与用来计算triplet loss与ID loss。正则化平衡了各个维度的。特征是超平面的高斯分布。这样的分布使得ID loss更容易收敛。此外，BNNeck减少了ID loss在的限制。ID loss更少的约束使得triplet loss同时更容易收敛。第三，正则化使得同一个人的特征更加紧密。

由于超平面相对于原始坐标来说几乎是对称的，BNNeck的另外一个trick是去除分类FC层的bias。这约束了分类超平面穿过原始坐标系。我们使用文献【4】中提出的初始化方法来初始化FC层。

在前向阶段，我们选择来进行行人ReID任务。Cosine距离会比欧氏距离的度量表现更好。表格1中的实验结果展示了BNNeck可以在很大程度上改善ReID模型的效果。

3.6 Center Loss

Triplet loss计算如下：

这里与分别表示正样本对与负样本对的特征距离。α是triplet loss的权重，等价于max(z,0)，本文中α设置为0.3。然而triplet loss只考虑与的区别，不考虑他们的绝对值。举个例子，当时，triplet loss为0.1。另外一个例子，当时，triplet loss也是0.1。triplet loss由两个新人目标随机采样得到。很难保证在整个训练数据集中。

Center loss【20】同时学习每一类的深度特征中心，将深度特征的距离与他们对应的类中心作为惩罚项，弥补了triplet loss的缺点。Center Loss函数公式表达如下：

这里表示mini-batch中第j张样本的标签。表示深度特征第个类的中心。B是batchsize的个数。公式形象的展示了类内变化。最小化center loss增加了类内紧密度。我们模型总共包括如下三个loss：

β是center loss的平衡权重。在我们的实验中β设置成了0.0005。