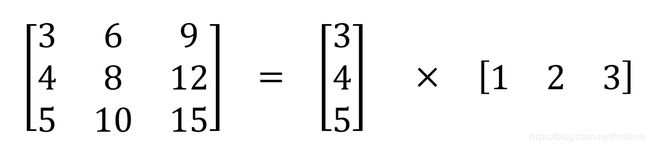Separable Convolutions: 可分离的卷积，让CNN再次伟大

1. 回顾传统 CNN 及它的不足之处

1.1 时间！时间！

传统的卷积神经网络已经在很多领域大显身手，在许多机器学习项目中取得了巨大的成就。但是它仍然存在一个最致命的问题——花费过大。

花费过大，主要体现在两种方面：

第一个方面是计算资源的消耗大
人们开玩笑说，深度学习到最后比的就是谁的孔方兄多，虽然有开玩笑的成分，但也不无道理。不过考虑到做项目的人往往都可以申请经费，最后花的是公家的钱，因此这个问题并不是最主要的问题——就算买不起豪华级别的显卡，也可以租一台云服务器用来跑算法嘛！能用钱解决的问题都不是问题。

真正处于瓶颈位置的问题，其实是第2个方面——也就是时间消耗过大。君不见随随便便跑一个算法，两三天都是好的，跑得慢一点的，甚至需要四五天、一个星期、半个月。也难怪人们把深度学习戏称为“炼丹术”，毕竟大家都没有绯红之王这种神器，跑算法的这段时间就只能像守着炼丹炉一样熬着，到最后才能看看算法效果怎么样。

奇怪，卷积神经网络不是号称什么“参数共享”“稀疏连接”，可以有效降低全连接网络的消耗吗？反正教学的时候各种听起来高大上的词给我们反复灌输CNN如何如何能减少参数，节省计算资源。听起来很勇的样子还是怎么像彬彬一样逊呢？

这个问题我们要从头开始考虑。

1.2 回顾：从 Dense 连接到 Conv 连接

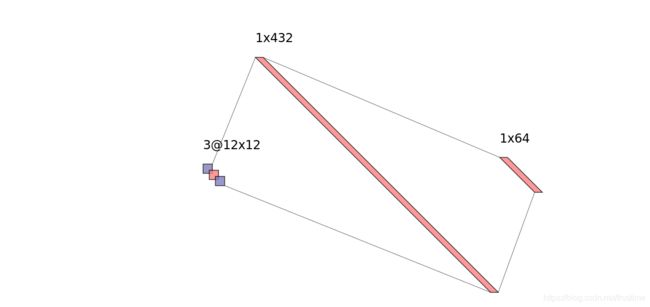
现在假设，我们不知道有 CNN 这种东西，而我们想要做一个简单的图像分类模型。输入是 $12\times 12\times 3$ 的图片，我们首先得把它展开成一个 432 维的向量，然后后面跟上一个 64 维的 hidden layer。网络的结构大致是下面这个样子的：

这个结构需要多少参数呢？我们在 keras 里面敲一敲：

input_layer = layers.Input(shape=(12, 12, 3))
flat = layers.Flatten()(input_layer)
hid = layers.Dense(64, use_bias=False)(flat)
model = keras.Model(input=input_layer, output=hid)
model.summary()

Model: "model_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 12, 12, 3)         0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 432)               0         
_________________________________________________________________
dense_1 (Dense)              (None, 64)                27648     
=================================================================
Total params: 27,648
Trainable params: 27,648
Non-trainable params: 0
_________________________________________________________________

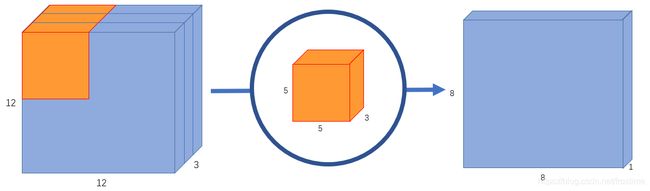
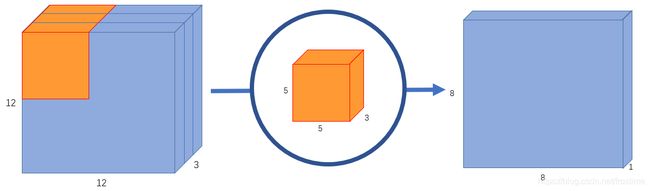
我去！这谁受得了？好在，后来我们知道了有卷积神经网络这么一个神奇的东西。于是我们把模型改成了这幅样子：

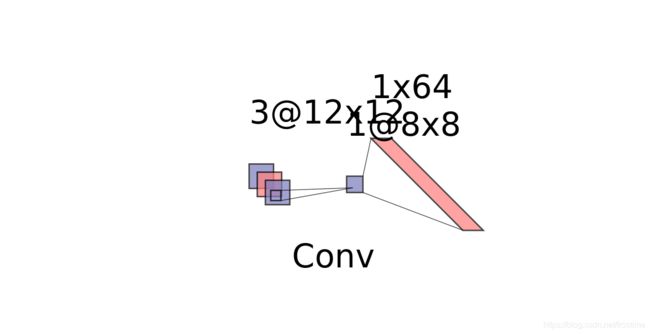
input_layer = layers.Input(shape=(12, 12, 3))
conv_layer = layers.Conv2D(1, (5, 5), use_bias=False)(input_layer)
flat = layers.Flatten()(conv_layer)
model = keras.Model(input=input_layer, output=flat)
model.summary()

Model: "model_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 12, 12, 3)         0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 8, 8, 1)           75        
_________________________________________________________________
flatten_1 (Flatten)          (None, 64)                0         
=================================================================
Total params: 75
Trainable params: 75
Non-trainable params: 0
_________________________________________________________________

注意到了吗？同样的输入，同样的输出，一个简单的 Conv 网络就把参数的数量从惨不忍睹的27648减到了75，“稀疏连接”恐怖如斯！由于神经网络的运算本质就是矩阵相乘，所以更少的参数，意味着更少的乘法、更少的时间开销。也正是因为传统的卷积神经网络层具有如此卓越的削减运算开销的功能，基于 CNN 的计算机视觉才能如火如荼的发展。

1.3 新时代、新挑战

我们现在来定量地考虑一个问题：上面两种网络分别需要多少的运算量？

首先看看全连接网络，Flatten 不算在计算中，所以核心的运算就是一个 $W_{64\times 432}\cdot x_{432\times 1}$ 的矩阵乘法，也就是 64 个 432 维向量乘以 432 维向量，也就是 $64\times (432\times 432)=11943936$
Dense 选手的表现很差劲呢。

下面来看卷积网络，同样 Flatten 是不算在计算量中的，所以我们抽出核心的卷积部分来分析。

一个 (5, 5, 3) 的卷积核，本身要做 $5\times 5\times 3=75$ 次的乘法操作，横着移动 8 次，竖着移动 8 次，一共是 $75\times 8\times 8=4800$ 次的乘法操作。

如果要输出 N 个通道，那么就是 $4800N$ 次乘法。

这个结果很好嘛？当然好了！把全连接和卷机两个一对比，简直就是数量级的差别，这是飞跃性的提升！
这个结果足够好吗？这就见仁见智了，如果是在10年前，我们会满心欢喜的接受这样的结果；但是10年后技术在不断发展，新的问题也在不断涌现。这时候我们再来看传统的卷积操作，就会有些不满了。因为处在新时代，我们处理的数据量越来越大、神经网络的层数越来越多，带来的结果是乘法运算的数量再次几何倍数地正常。尽管传统的CNN和单纯的全连接相比有了质的提升，但是越来越无法满足我们现在的需要。

现在我们再一次回到了 1.1 节，那一节的标题是“时间！时间！”。明白是什么意思了嘛？

面对这样的窘境，不少人开启了新的思考：既然从全连接层到传统的卷积层，我们削减了计算的开支；那我们能不能进一步改进网络，让它的计算量进一步的减少呢？

答案是——Separable Convolutions。

2. Separable Convolutions

Separable Convolutions，顾名思义，是“可分离”的卷积神经网络。有的童鞋可能就纳闷了：

干嘛叫 Separable?

在正式讲separable convolutions之前，我想谈一谈这个问题，因为我觉得这个方法的所体现出来的哲理具有一定的普适性。

以下部分是我自己的思考（胡诌），算是从一个感性的方面来认识所谓的 Separable 这个词。嫌我啰嗦的童鞋手动跳过。

---

我还记得在我小学的时候，有一天老师出了这样一道题，已知从北京到上海有多少多少种走法，从上海到广州又有多少多少种走法，那么从北京到上海再到广州有几种走法呢？
那时傻乎乎的我把从北京到上海再从上海到广州的路一条一条的列了出来，然而还没等我在草稿纸上列完，同桌就已经抢先报出答案了，算法很简单，把两个数字乘起来就行了。

这虽然是一个简单的小故事，但是其中却蕴含了一个深刻的哲理。那就是合而虑之，不如分而治之。这个道理在我进入大学学习计算机以后愈加的凸显——为了降低系统的复杂度，我们进行了模块化；为了简化问题的分析难度，我们使用了数学归纳法；为了提高系统的安全性，我们选择了去中心。

可以看到，“分”这个字简直有一股奇怪的魔力，任何东西只要一分，马上就不一样了。古人云“三个臭皮匠，顶一个诸葛亮”。虽然三个臭皮匠加起来可能都不如诸葛亮，却胜在普遍；昭烈皇帝三顾茅庐方得卧龙出山，而找三个臭皮匠却何其简单。

Separate，本质上就是把一个耦合严重的系统分离成多个高内聚低耦合的模块，多个模块组合在一起，比原来拧成一坨更精简高效。
——我说的

我仔细思考了如何利用 Separate 来做优化，我认为其中内在的道理和思路是这样的：

1. 给定一个任务 $O(N)$
2. 把 $O(N)$ 建模为 $O(P\times Q)$
3. 想办法变成 $O(P+Q)$

仔细观察，你会发现 Separable Convolutions 完美符合这个思路。

---

好了，废话完毕。现在我们来考虑怎么分解卷积操作，首先要搞清楚的问题卷积操作的过程是什么样的？$O(N)$到底是个什么东西？

1. 卷积核放在image上
2. 卷积核对 channel 1、2、3分别做卷积
3. 卷积核在 image 上移动

我们发现，卷积操作涉及到了两个维度：

1. 空间维度，卷积核是如何在一个 image 上跑来跑去的
2. 深度维度，卷积核在不同深度的 channel 上依次做卷积操作

两种维度，提供两种视角，基于两种不同的视角，人们提出了两种不同的 Separable Convolution 方法。

• 基于空间视角，人们提出了 Spatial Separable Convolutions
• 基于深度视角，人们提出了 Depthwise Separable Convolutions

2.1 Spatial Separable Convolutions

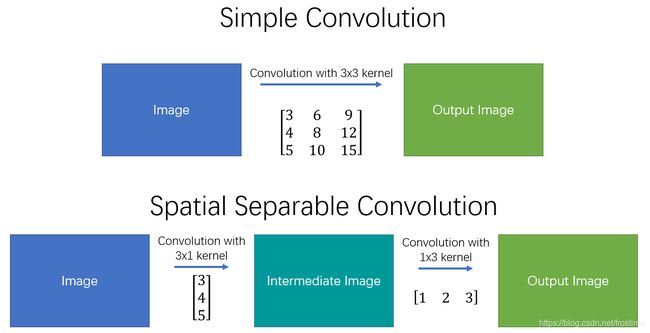
在这个视角下，人们尝试着 将卷积核分解为若干个小卷积核。譬如，我们可以将卷积核分解为两个（或者若干个）向量的外积，如下图所示：

怎么用呢？如下图所示，我们在原来的 image 上先用 kern1 做一次卷积，然后再在得到的结果上用 kern2 做一次卷积操作。

我们还是以之前 (12, 12, 3) 的图像举例，这次我们不用 (5, 5) 的卷积核，而是分别用两个维度为 5 的行列向量作为卷积核，看看效果如何：

input_layer = layers.Input(shape=(12, 12, 3))
conv1 = layers.Conv2D(1, (5, 1), use_bias=False)(input_layer)
conv2 = layers.Conv2D(1, (1, 5), use_bias=False)(conv1)
flat = layers.Flatten()(conv2)
model = keras.Model(input=input_layer, output=flat)
model.summary()

Model: "model_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 12, 12, 3)         0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 8, 12, 1)          15        
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 8, 8, 1)           5         
_________________________________________________________________
flatten_1 (Flatten)          (None, 64)                0         
=================================================================
Total params: 20
Trainable params: 20
Non-trainable params: 0
_________________________________________________________________

之前是 75，这一下变成了 20。输入输出的维度都没变，参数数量却只有原来的 1/3 ！那么乘法运算量变化如何？

显然，第一次的卷积需要用到 $(5\times 1\times 3)\times (8\times 12)=1440$；第二次卷积需要 $(1\times 5\times 3)\times (8\times 8)=960$。所以总共需要 $1440+960=2400$次。有了可观的削减。

但是有个坏消息：从实际情况而言，并不是所有的卷积核都可以被有效地分解为几个更小的卷积核的。所以这种卷积方法用的也不多[1]。

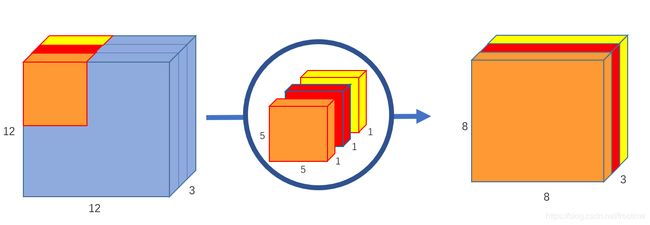
2.2 Depthwise Separable Convolutions

同 Spatial 相比，Depthwise 的可分离卷积网络着眼于 channel 这个维度。

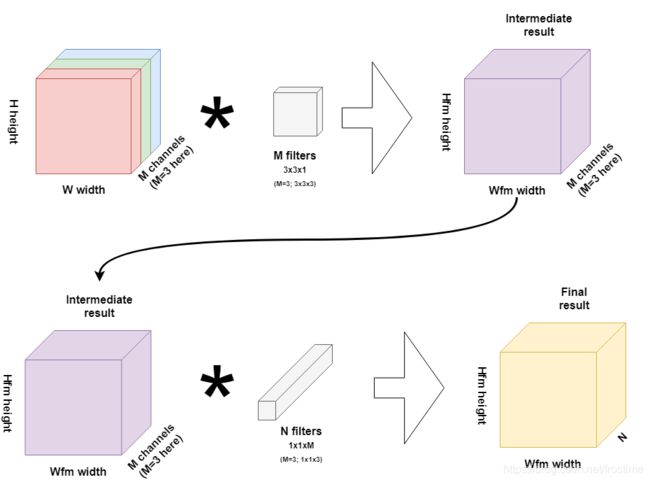
现在假定一个完整的卷积操作可以把一个 $H\times W\times C$ 的图像转变为$H^{\prime }\times W^{\prime }\times N$的输出，其中 (H, W) 是图像的尺寸， C 是输入的通道，通常是 RGB 为3； N 则是输出的通道。DSC 把一个完整的卷积过程分成了两步：

1. Depthwise convolutions

$H\times W\times C\Rightarrow H^{\prime }\times W^{\prime }\times C$

2. Pointwise convolutions

$H^{\prime }\times W^{\prime }\times C\Rightarrow H^{\prime }\times W^{\prime }\times N$

2.2.1 Depthwise convolutions

首先来回忆一下，传统的卷积的做法是不是每个卷积核一次性处理所有通道？就像这样：

Ok，DC 换了一种做法：一个卷积核只处理一个通道。
等等？一次只处理一个通道？这要怎么搞？那么我要使用多个卷积核使得输出有多个通道的时候该去处理哪个输入通道呢？

因为这只是 DSC 的第一步啊！都说了 Separable 了嘛！所以第一步就只考虑 In-Channels ，至于 Out-Channels 是第二步要考虑的。

Depthwise convolutions 做的事情只有一个：用 C （channels）个卷积核分别作用在图像的各个通道上：

keras里面有 DepthwiseConv 的 API，我们可以看一下效果如何：

input_layer = layers.Input(shape=(12, 12, 3))
conv1 = layers.DepthwiseConv2D((5, 5), use_bias=False)(input_layer)
model = keras.Model(input=input_layer, output=conv1)
model.summary()

Model: "model_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 12, 12, 3)         0         
_________________________________________________________________
depthwise_conv2d_1 (Depthwis (None, 8, 8, 3)           75        
=================================================================
Total params: 75
Trainable params: 75
Non-trainable params: 0
_________________________________________________________________

3 个卷积核，每个都是 (5, 5)，所以 75 个参数。

注意到：

1. DepthwiseConv2D 不需要指定 filters 也就是卷积核的数量参数，因为这个数量只会和输入的通道数量相同
2. 输出的 shape 为 (8, 8, 3) ，显然只改变了宽高并不改变通道

所以说，这一步完成了$H\times W\times C\Rightarrow H^{\prime }\times W^{\prime }\times C$的操作。

2.2.2 Pointwise convolutions

DepthwiseConv 后就是 Pointwise Conv。其实，别看叫得那么玄乎，这一步做的工作也很简单，就是用 (1, 1) 的卷积核在上一步的输出上做标准的卷积操作，就像这样：

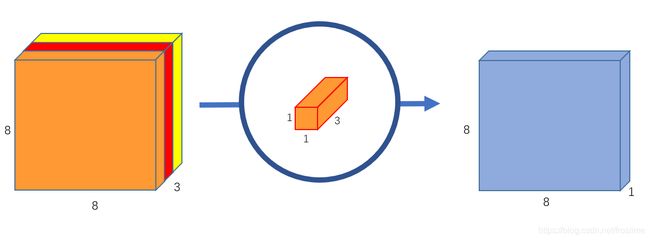
输出的只有一个通道，想要多个通道怎么办？很简单，用 N 个 1 x 1 卷积核就行了。

这一步完成了$H^{\prime }\times W^{\prime }\times C\Rightarrow H^{\prime }\times W^{\prime }\times N$的操作。

2.2.3 把两步加起来

把两步加起来，就得到了 Depthwise Separable Convolutions。

在 keras 中有现成的 SeparableConv API，完成了 DSC 的功能（然而没有 Spatial……），我们再来试一次：

input_layer = layers.Input(shape=(12, 12, 3))
conv1 = layers.SeparableConv2D(1, (5, 5), use_bias=False)(input_layer)
model = keras.Model(input=input_layer, output=conv1)
model.summary()

Model: "model_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 12, 12, 3)         0         
_________________________________________________________________
separable_conv2d_1 (Separabl (None, 8, 8, 1)           78        
=================================================================
Total params: 78
Trainable params: 78
Non-trainable params: 0
_________________________________________________________________

第一步 75 个参数；第二步中一个 (1, 1, 3) 的卷积核；一共 78 个参数。

那么，需要用到多少次的乘法运算呢？

首先第一步中，一共是 $((5\times 5)\times (8\times 8))\times 3=4800$次；第二步中，需要 $(3\times 8\times 8)\times N$次，所以一共是 $4800+192N$次。

还记得原始的卷积神经网络需要多少吗？$4800N$！我们成功地把 $O(P\times Q)$变成了 $O(P+Q)$！

Nice Job!

然而不要太得意，我们要注意到，4800N 并不是永远都比 4800 + 192N 大的，虽然二者在算法复杂度上确实有差距，但如果想让优化后的差距产生明显的效果，前提是 N 要足够大！这就意味着，DSC 只有在网络结构足够复杂时才能大显身手；如果网络结构本身很简单，那么使用 DSC 反而会拖后腿，这就是需要权衡的了！

总结

Separable Convolutions makes CNN GREAT AGAIN!!!

Reference

[1]
Chi-Feng Wang, 《A Basic Introduction to Separable Convolutions》, 24-4月-2018. [在线]. 载于: https://towardsdatascience.com/a-basic-introduction-to-separable-convolutions-b99ec3102728.

[2]
Chris, 《Creating depthwise separable convolutions in Keras》, 24-9月-2019. [在线]. 载于: https://www.machinecurve.com/index.php/2019/09/24/creating-depthwise-separable-convolutions-in-keras/.

[3]
Chris, 《Understanding separable convolutions》, 23-9月-2019. [在线]. 载于: https://www.machinecurve.com/index.php/2019/09/23/understanding-separable-convolutions/.