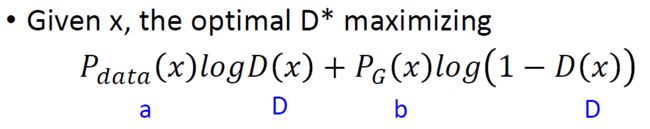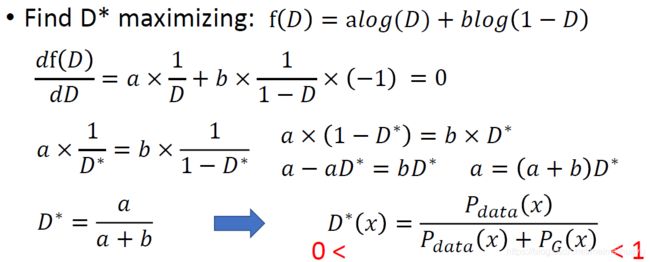生成对抗网络原始文章算法详细介绍

生成对抗网络的基本思想：

生成对抗网络中有两个模型Generator和Discriminator,生成模型可以比作counterfeiters，判别模型可以比做是police，生成模型通过自身的优化产生越来越像真钞的假币

，而判别模型也通过对自身不断的优化提高自己判别假币的能力，两者相互对抗，直到仿品不能从真品中分辨出来。

生成模型：

比如一个图片的生成输入是高维的vector，输出为图片

判别模型：输入为一张图片，输出一个标量值，判别器会给来自training 数据集的image高分，而对来自generator的image一个低分值

上图是生成对抗网络中给的图解释如下：

蓝色是D

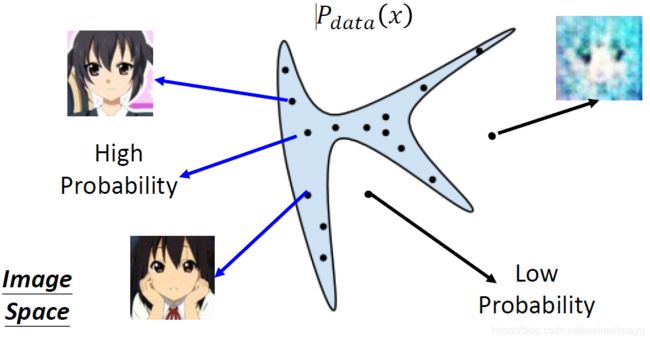
黑色圆点是Pdata分布

绿色实线是Pg

图a中D给来自Pdata中的数据给高分，来自G的数据低分

图b中在训练过程中迭代。

图c中，G根据判别器给的分不断调整G使得Pg接近Pdata

图d当当两者分布一致时，判别器没有坏掉，不起判别作用

生成对抗网络的基本原理：

假如x是一张图片，在这张图片内部有很多种分布，但是在上面的图片中蓝色的区域有很高的概率表示一张图片，蓝色以外的部分的分布产生的图片往往是模糊的（很低的概率），所以我们就试图找到蓝色区域的分布Pdata（x）

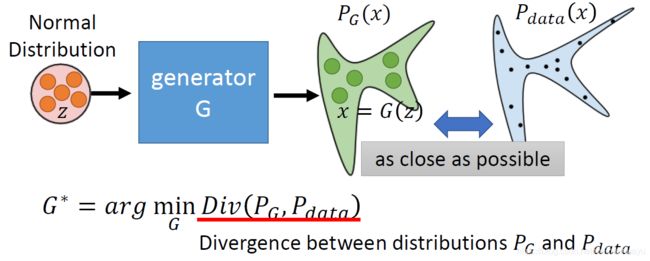
但是想要找到这样的分布十分的困难，只能从Pdata中采样，然后用最大似然法不断的逼近原始分布。（生成对抗网络从一个先验的分布中采样）

最大似然等价于最小化KL divergence衡量两个分布之间的的差异，越小说明两个分布之间的差异越小

 

 

所以求最大似然的过程就变成求两个分布之间的divergence的问题，但是目前Pdata和Pg我们都不知道，因为Pdata可以从training数据中采样从而得到分布，但是Pg是不能从任何分布中得到的，所以我们不能事先给定一个固定的分布因为：

假设我们的Pg只是一个高斯分布，那么其有很多的限制，我们希望Pg是一个一般化的分布，可以不是高斯，也可以是比高斯分布更复杂的分布，但是如果他比高斯更复杂，我们将不能计算他的最大似然？

那么我们如何定义一个一般化的Pg?

如果把generator定义成一个network则可以产生任何形式的分布：因为network内部有很多hidden layer，所以他可以产生任何的一些复杂的分布，我们就可以根据网络产生的分布和原始training数据的分布作比较。

 

那么问题变成：怎样计算Pg和Pdata两者的Divergence？

生成对抗网络通过Discriminator计算两者之间的divergence（为什么Disriminator可以用来用来计算两者间的divergence呢？）

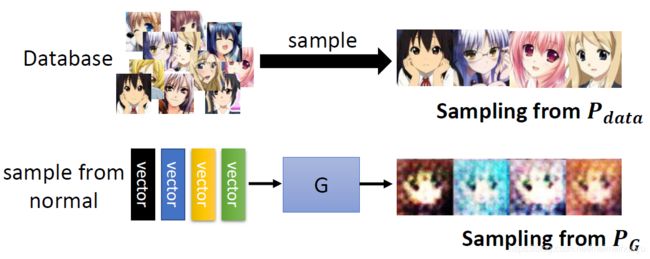
虽然我们事先都不知道Pg和Pdata的分布，但是我们可以采样：

判别模型对于来自database的数据给高分，来自生成模型的数据给低分

 

 

根据训练的目标函数：训练Disrimimator的过程为：将从Pdata的数据x通过D，并给其高分，将从Pg中抽取的数据x通过D并给其低分，以使得目标函数最大，Discrimimator实际上是一个二分类的分类器。

那么为什么这样的Discriminator可以表示两个分布之间的Divergence呢？

proof如下：

如下图当两个分布很接近的时候，其divergence很小，而这样的两个分布中通过Discriminator的时候也很难得到小的目标函数值，如果两个分布之前相差跟大，divergence很大，Discriminator的目标函数的值也很大

所以我们优化的D的目标函数的时候，其实就是找到使得两个分布的divergence最大的D

找G的过程就是找使得两个分布的divergence最小的那个那个G

所以生成对抗网络是一个极小化极大值的游戏

 

上面讨论了通过计算Discriminator的目标函数可以得到两个分布之间的divergence，那么如何计算这个目标函数

上图中，通过假设D(x)是任意的函数，那么input一个x，他可以输出任意的值，所以对于

中括号的式子带不同的x再求和

把某个x拿出来，然后找一个D，保证式子

的值越大越好，所有不同的x分开算

 

那么现在的问题变成怎样找到这样的D(x)?

方法是把D(x)当做自变量，然后对其求梯度，在梯度等于0的时候找到最大的D*

为什么又进一步说求目标函数的过程是求JS divergence？proof：

 

 

以上证明Discrimimator实际上是求两个分布之间的divergence（JS divergence）所以在找最佳Generator的时候：

 

等于：

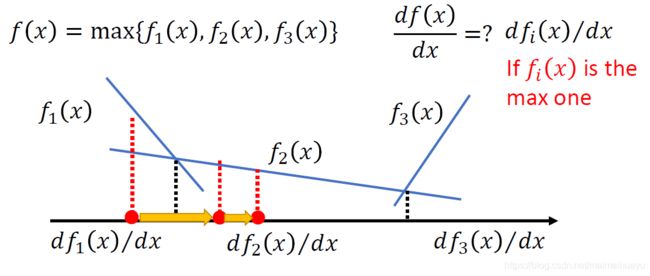
上图三条曲线的解释为：对于固定的G找到最大的V,然后对于所有的G找到使得max V最小的那个，图片中符合条件的是G3

 

2014年生成对抗网络文章中算法的介绍：

算法的初始化：对生成器和判别器分别给初值

 

首先固定G对L(G)求参数：（为什么带有max的函数可以求梯度呢？）

为什么可以对含有max的函数求梯度是可行的？

L(G)是一个函数的集合，对其求梯度是可能的，proof如下：对每个函数，f在这一区间是做大的，则对其求梯度

 

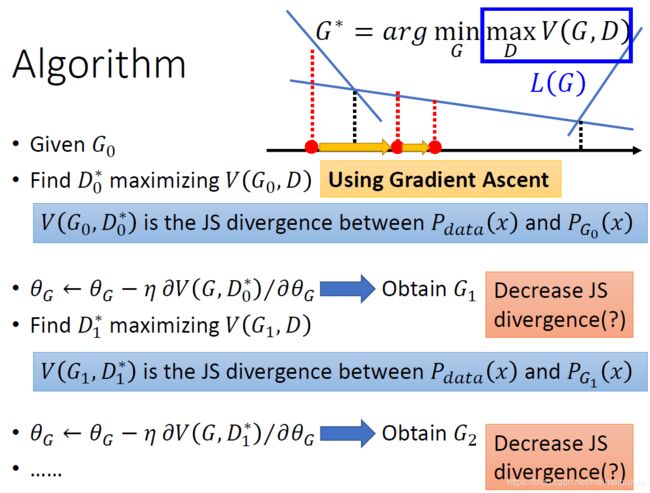
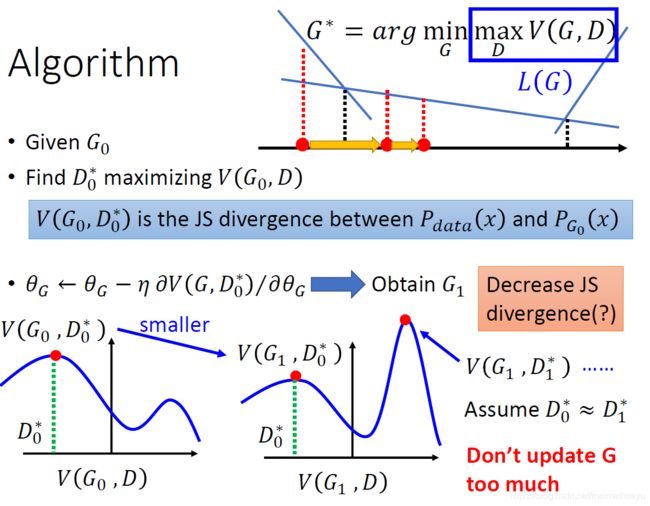
首先固定G然后，找到迭代找到最适合的D*，（寻找D*的过程是类似于二分类中找到最优的判别器）然后在更新G的时候用D*去当裁判

按照上图中给定的算法步骤，能确定每次都减少Decrease JS divergence呢，实际上，不一定每次都是减少了这个值，proof如下：

图中G2的divergence并不比G0中的小，原因在于G1并不是G2,我们在每次迭代中都改变了G，所以在实际的操作中我们是假设G是非常像的

并且不能频繁更新G

 

完整算法：

总结：

根据上述描述：

0.对于Pdata和Pg我们事先并不知道他的分布，但是我们可以通过采样获得分布

1.生成对抗模型包含两个网络，Generator和Disriminator，而且两个都为neural nework

2.Generator负责生成分布，使得分布不断接近training数据的分布

3.Disriminator负责判别数据是来自training数据还是来自generator，并给来自training的数据高分，来自generator的数据低分

4.D的目标实际上是最大化两个分布的JS divergence

5.算法在训过程中是先固定G然后找到最优的D，然后用这个最优的D去判别G得到新的G(D在训练过程中迭代k次,然而G不能频繁更新）

以上图片来自2014年的文章 https://arxiv.org/abs/1406.2661

以及李宏毅老师的课件： http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS18.html