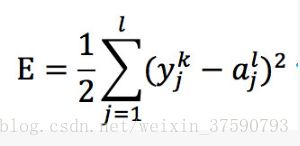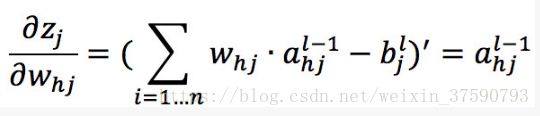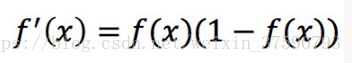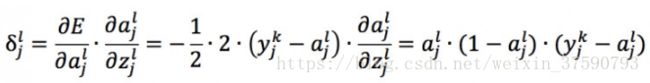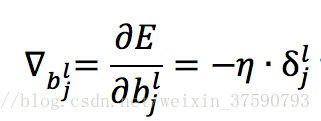盒马唠机器学习之BP神经网络
对于大多数的人来说刚接触神经网络的时候都会先碰到BP算法的问题,如何形象快速地理解BP神经网络,尤其是理解当中的逆向反馈,很多人总是会在这里的大量公式觉得好像很难就退缩了,其实不难,就是一个链式求导法则反复用。如果不想看公式,可以直接把数值带进去,实际的计算一下,体会一下这个过程之后再来推导公式,这样就会觉得很容易了。
神经网络的结构
神经网络由大量的节点(或称神经元)之间相互联接构成,每个节点代表一种特定的输出函数,称为激活函数(activation function);每两个节点间的连接都代表一个对于通过该连接信号的加权值,称之为权重(weight),神经网络就是通过这种方式来模拟人类的记忆。网络的输出则取决于网络的结构、网络的连接方式、权重和激活函数。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达,是对传统逻辑学演算的进一步延伸。
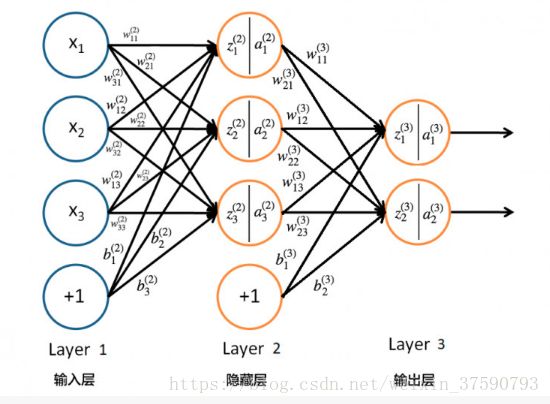
下面,我们通过上面的3层的神经网络去推导神经网络,里面有输入层、一个隐藏层和一个输出层。除了输入层的神经元,每个神经元都会有加权求和得到的输入值 z 和将 z 通过 Sigmoid 函数(也即是激活函数)非线性转化后的输出值 a,他们之间的计算公式如下:
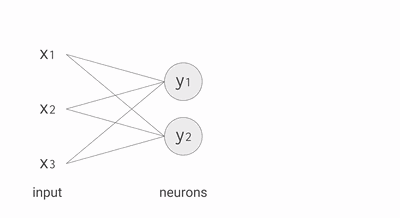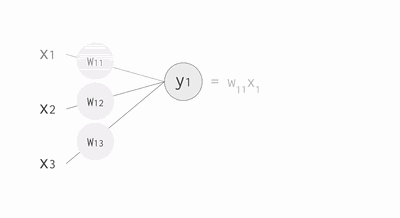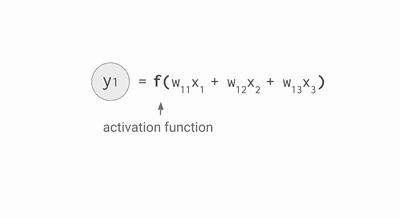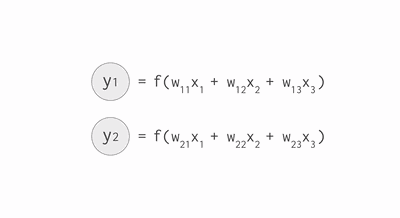
其中,公式里面的变量l和j表示的是第l层的第 j 个神经元,ij 则表示从第 i 个神经元到第 j 个神经元之间的连线,w 表示的是权重,b 表示的是偏置,后面这些符号的含义大体上与这里描述的相似,所以不会再说明。下面的 Gif 动图可以更加清楚每个神经元输入输出值的计算方式(注意,这里的动图并没有加上偏置,但使用中都会加上)
激活函数
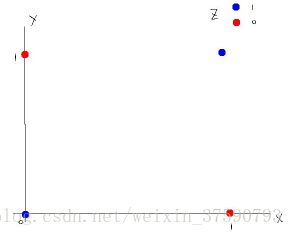
使用激活函数的原因是因为线性模型(无法处理线性不可分的情况)的表达能力不够,所以这里通常需要加入 Sigmoid 函数来加入非线性因素得到神经元的输出值。为啥线性模型(无法处理线性不可分的情况)的表达能力不够呢?我下面简单的说下。某些数据是线性可分的,意思是,可以用一条直线将数据分开。比如下图:
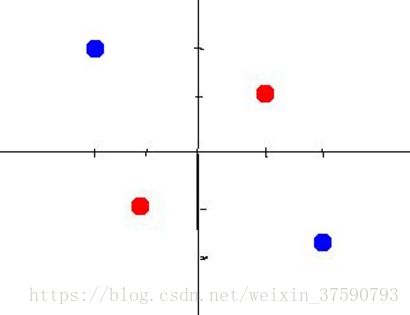
但是有些数据不是线性可分的。比如如下数据:
第二组数据你就没有办法画出一条直线来将数据区分开。这时候有两个办法,第一个办法,是做线性变换(linear transformation),比如讲x,y变成x^2,y^2,这样可以画出圆形。如图所示:
你会发现数据经过这样的变换后是线性可分的了。
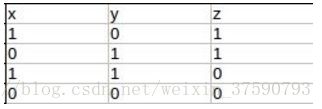
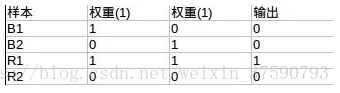
另外一种方法是引入非线性函数。我们来看异或问题(xor problem)。以下是xor真值表
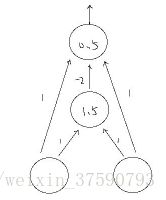
我们也可以设计一种神经网络,通过激活函数来使得这组数据线性可分。激活函数我们选择阀值函数,也就是大于某个值输出1(被激活了),小于等于则输出0(没有激活)。这个函数是非线性函数。
其中直线上的数字为权重。圆圈中的数字为阀值。第二层,如果输入大于1.5则输出1,否则0;第三层,如果输入大于0.5,则输出1,否则0.
第一层到第二层(阀值1.5)
第二层到第三层(阀值0.5)
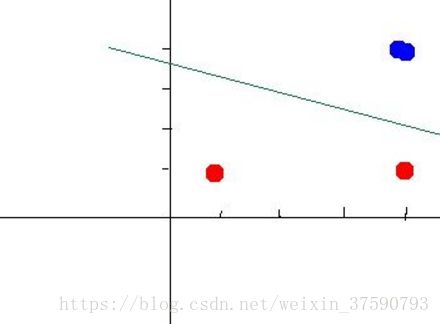
可以看到第三层输出就是我们所要的xor的答案。经过变换后的数据是线性可分的(n维,比如本例中可以用平面),如图所示:
总而言之,激活函数可以引入非线性因素,解决线性模型所不能解决的问题。如果不加入激活函数,啧啧,估计大家都可以发现了,不管神经网络的权值怎么组合,最多就是线性方程的组合,最后得到的分类器本质还是一个线性方程,该处理不了的非线性问题,它还是处理不了。
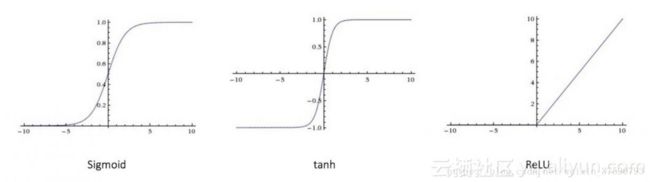
激活函数(Activation function),不要误解是指这个函数去激活什么,而是指如何把“激活的神经元的特征”通过函数把特征保留并映射出来,这是神经网络能解决非线性问题关键。激活函数众所周知有tanh,sigmoid和ReLU等。
tanh(双切正切函数),取值范围[-1,1]。
sigmoid采用S形函数,取值范围[0,1]。
ReLU简单而粗暴,大于0的留下,否则一律为0。
因为神经网络的数学基础是处处可微的,所以选取的激活函数要能保证数据输入与输出也是可微的。神经网络中,运算特征是不断进行循环计算,所以在每代循环过程中,每个神经元的值也是在不断变化的。这就导致了tanh特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果显示出来。但有时候,特征相差比较复杂或是相差不是特别大时,需要更细微的分类判断的时候,sigmoid效果就好了。而Relu,它就是取的max(0,x),因为神经网络是不断反复计算,实际上变成了它在尝试不断试探如何用一个大多数为0的矩阵来尝试表达数据特征,结果因为稀疏特性的存在,反而这种方法变得运算得又快效果又好了。所以,目前大多在用max(0,x)来代替sigmod函数了。
本文是通过sigmod函数去讲神经网络的。
BP 算法执行的流程(前向传递和逆向更新)
在手工设定了神经网络的层数,每层的神经元的个数,学习率 η(下面会提到)后,BP 算法会先随机初始化每条连接线权重和偏置,然后对于训练集中的每个输入 x 和输出 y,BP 算法都会先执行前向传输得到预测值,然后根据真实值与预测值之间的误差执行逆向反馈更新神经网络中每条连接线的权重和每层的偏好。在没有到达停止条件的情况下重复上述过程。
其中,停止条件可以是权重的更新低于某个阈值的时候、预测的错误率低于某个阈值和达到预设一定的迭代次数。
例如,譬如说,手写数字识别中,一张手写数字1的图片储存了28*28 = 784个像素点,每个像素点储存着灰度值(值域为[0,255]),那么就意味着有784个神经元作为输入层,而输出层有10个神经元代表数字0~9,每个神经元取值为0~1,代表着这张图片是这个数字的概率。每输入一张图片(也就是实例),神经网络会执行前向传输一层一层的计算到输出层神经元的值,根据哪个输出神经元的值最大来预测输入图片所代表的手写数字。然后根据输出神经元的值,计算出预测值与真实值之间的误差,再逆向反馈更新神经网络中每条连接线的权重和每个神经元的偏好。
在讲前向传输和逆向反馈的时候,我们先将前面的3层神经网络图和对应的公式复制下来方便对照。
前向传输(Feed-Forward)
从输入层=>隐藏层=>输出层,一层一层的计算所有神经元输出值的过程。
逆向反馈(Back Propagation)
因为输出层的值与真实的值会存在误差,我们可以用均方误差来衡量预测值和真实值之间的误差。
逆向反馈的目的就是让E函数的值尽可能的小,而每个神经元的输出值是由该点的连接线对应的权重值和该层对应的偏好所决定的,因此,要让误差函数达到最小,我们就要调整w和b值, 使得误差函数的值最小。
其中 η 为学习率,取值通常为 0.1 ~ 0.3,可以理解为每次梯度所迈的步伐。注意到 w_hj 的值先影响到第 j 个输出层神经元的输入值a,再影响到输出值y,根据链式求导法则有:
目标函数 E 求 w 和 b 的偏导可以得到 w 和 b 的更新量(其本质就是梯度下降),下面拿求 w 偏导来做推导。要注意了下面的说难不难,说简单又不简单。其主要的原理就是链式求导法则:
根据神经元输出值 a 的定义有:
Sigmoid 求导数的式子如下,从式子中可以发现其在计算机中实现也是非常的方便:
所以
则权重 w 的更新量为:
类似可得 b 的更新量为:
但这两个公式只能够更新输出层与前一层连接线的权重和输出层的偏置,原因是因为 δ 值依赖了真实值y这个变量,但是我们只知道输出层的真实值而不知道每层隐藏层的真实值,导致无法计算每层隐藏层的 δ 值,所以我们希望能够利用 l+1 层的 δ 值来计算 l 层的 δ 值,而恰恰通过一些列数学转换后可以做到,这也就是逆向反馈名字的由来,公式如下:
在推导之前请先观察下面这张图:
首先我们看到 l 层的第 i 个神经元与 l+1 层的所有神经元都有连接,那么我们可以将 δ 展开成如下的式子:
也即是说我们可以将 E 看做是 l+1 层所有神经元输入值的 z 函数,而上面式子的 n 表示的是 l+1 层神经元的数量,再进行化简后就可以得到上面所说的式子。
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
network.py
~~~~~~~~~~
A module to implement the stochastic gradient descent learning
algorithm for a feedforward neural network. Gradients are calculated
using backpropagation. Note that I have focused on making the code
simple, easily readable, and easily modifiable. It is not optimized,
and omits many desirable features.
"""
#### Libraries
# Standard library
import random
# Third-party libraries
import numpy as np
class Network(object):
def __init__(self, sizes):
"""
:param sizes: list类型,储存每层神经网络的神经元数目
譬如说:sizes = [2, 3, 2] 表示输入层有两个神经元、
隐藏层有3个神经元以及输出层有2个神经元
"""
# 有几层神经网络
self.num_layers = len(sizes)
self.sizes = sizes
# 除去输入层,随机产生每层中 y 个神经元的 biase 值(0 - 1)
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
# 随机产生每条连接线的 weight 值(0 - 1)
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
def feedforward(self, a):
"""
前向传输计算每个神经元的值
:param a: 输入值
:return: 计算后每个神经元的值
"""
for b, w in zip(self.biases, self.weights):
# 加权求和以及加上 biase
a = sigmoid(np.dot(w, a) + b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""
随机梯度下降
:param training_data: 输入的训练集
:param epochs: 迭代次数
:param mini_batch_size: 小样本数量
:param eta: 学习率
:param test_data: 测试数据集
"""
test_data = list(test_data)
training_data = list(training_data)
if test_data: n_test = len(test_data)
n = len(training_data)
for j in range(epochs):
# 搅乱训练集,让其排序顺序发生变化
random.shuffle(training_data)
# 按照小样本数量划分训练集
mini_batches = [
training_data[k:k+mini_batch_size]
for k in range(0, n, mini_batch_size)]
for mini_batch in mini_batches:
# 根据每个小样本来更新 w 和 b,代码在下一段
self.update_mini_batch(mini_batch, eta)
# 输出测试每轮结束后,神经网络的准确度
if test_data:
print("Epoch {%d}: {%d} / {%d}"%(j, self.evaluate(test_data), n_test))
else:
print ("Epoch {%d} complete"%(j))
def update_mini_batch(self, mini_batch, eta):
"""
更新 w 和 b 的值
:param mini_batch: 一部分的样本
:param eta: 学习率
"""
# 根据 biases 和 weights 的行列数创建对应的全部元素值为 0 的空矩阵
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
# 根据样本中的每一个输入 x 的其输出 y,计算 w 和 b 的偏导数
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
# 累加储存偏导值 delta_nabla_b 和 delta_nabla_w
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
# 更新根据累加的偏导值更新 w 和 b,这里因为用了小样本,
# 所以 eta 要除于小样本的长度
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""
:param x:
:param y:
:return:
"""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# 前向传输
activation = x
# 储存每层的神经元的值的矩阵,下面循环会 append 每层的神经元的值
activations = [x]
# 储存每个未经过 sigmoid 计算的神经元的值
zs = []
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# 求 δ 的值
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
# 乘于前一层的输出值
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
for l in range(2, self.num_layers):
# 从倒数第 **l** 层开始更新,**-l** 是 python 中特有的语法表示从倒数第 l 层开始计算
# 下面这里利用 **l+1** 层的 δ 值来计算 **l** 的 δ 值
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
# 获得预测结果
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
# 返回正确识别的个数
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
"""
二次损失函数
:param output_activations:
:param y:
:return:
"""
return (output_activations-y)
#### Miscellaneous functions
def sigmoid(z):
"""
求 sigmoid 函数的值
:param z:
:return:
"""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""
求 sigmoid 函数的导数
:param z:
:return:
"""
return sigmoid(z)*(1-sigmoid(z))
"""
mnist_loader
~~~~~~~~~~~~
A library to load the MNIST image data. For details of the data
structures that are returned, see the doc strings for ``load_data``
and ``load_data_wrapper``. In practice, ``load_data_wrapper`` is the
function usually called by our neural network code.
"""
#### Libraries
# Standard library
import pickle
import gzip
# Third-party libraries
import numpy as np
def load_data():
"""Return the MNIST data as a tuple containing the training data,
the validation data, and the test data.
The ``training_data`` is returned as a tuple with two entries.
The first entry contains the actual training images. This is a
numpy ndarray with 50,000 entries. Each entry is, in turn, a
numpy ndarray with 784 values, representing the 28 * 28 = 784
pixels in a single MNIST image.
The second entry in the ``training_data`` tuple is a numpy ndarray
containing 50,000 entries. Those entries are just the digit
values (0...9) for the corresponding images contained in the first
entry of the tuple.
The ``validation_data`` and ``test_data`` are similar, except
each contains only 10,000 images.
This is a nice data format, but for use in neural networks it's
helpful to modify the format of the ``training_data`` a little.
That's done in the wrapper function ``load_data_wrapper()``, see
below.
"""
f = gzip.open('E:/机器学习与深度学习/mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = pickle.load(f,encoding='iso-8859-1')
f.close()
return (training_data, validation_data, test_data)
def load_data_wrapper():
"""Return a tuple containing ``(training_data, validation_data,
test_data)``. Based on ``load_data``, but the format is more
convenient for use in our implementation of neural networks.
In particular, ``training_data`` is a list containing 50,000
2-tuples ``(x, y)``. ``x`` is a 784-dimensional numpy.ndarray
containing the input image. ``y`` is a 10-dimensional
numpy.ndarray representing the unit vector corresponding to the
correct digit for ``x``.
``validation_data`` and ``test_data`` are lists containing 10,000
2-tuples ``(x, y)``. In each case, ``x`` is a 784-dimensional
numpy.ndarry containing the input image, and ``y`` is the
corresponding classification, i.e., the digit values (integers)
corresponding to ``x``.
Obviously, this means we're using slightly different formats for
the training data and the validation / test data. These formats
turn out to be the most convenient for use in our neural network
code."""
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = zip(validation_inputs, va_d[1])
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return (training_data, validation_data, test_data)
def vectorized_result(j):
"""Return a 10-dimensional unit vector with a 1.0 in the jth
position and zeroes elsewhere. This is used to convert a digit
(0...9) into a corresponding desired output from the neural
network."""
e = np.zeros((10, 1))
e[j] = 1.0
return e
training_data, validation_data, test_data = load_data_wrapper()
net = Network([784, 30, 10])
net.SGD(training_data, 30, 10, 3.0, test_data = test_data)