神经网络常见优化算法(Momentum, RMSprop, Adam)的原理及公式理解, 学习率衰减
参考资料: 吴恩达Coursera深度学习课程 deeplearning.ai (2-2) 优化算法–课程笔记
1. 指数加权平均(指数加权移动平均)

指数加权平均是统计一个波动的指标在一段时间内的平均变化趋势, 具体公式为: v t = β v t − 1 + ( 1 − β ) θ t v_t = \beta v_{t-1} + (1 - \beta)\theta_t vt=βvt−1+(1−β)θt其中 β \beta β是对过去的权重, ( 1 − β ) (1-\beta) (1−β)是对当前值的权重, 两者之和就是对一个变化指标的移动加权平均.
结果大体相当于平均了近 1 ( 1 − β ) \frac{1}{(1-\beta)} (1−β)1天的值, 例如 β = 0.95 \beta = 0.95 β=0.95相当于平均了近20天的值, β = 0.9 \beta = 0.9 β=0.9相当于平均了近10天的值.
解释: 如下图
因为 β 1 ( 1 − β ) = 1 e ≈ 1 3 \beta ^{\frac{1}{(1-\beta)}} = \frac{1}{e} \approx \frac{1}{3} β(1−β)1=e1≈31
所以权重小于 0.1 ∗ β 1 ( 1 − β ) 0.1 * \beta ^{\frac{1}{(1-\beta)}} 0.1∗β(1−β)1的数据我们可以忽略不计, 得到的就是平均了近 1 ( 1 − β ) \frac{1}{(1-\beta)} (1−β)1天的值.
偏差修正
由于加权平均的前期, 历史数据不足, 所以前期的数值会非常小, 需要进行偏差修正:
v t = β v t − 1 + ( 1 − β ) θ t v_t = \beta v_{t-1} + (1 - \beta)\theta_t vt=βvt−1+(1−β)θt v t = v t 1 − β t v_t = \frac{v_t}{1-\beta^t} vt=1−βtvt经过修正后, 前期的值不再变得很小, 并且后期 ( 1 − β t ) (1-\beta^t) (1−βt)的值趋向于1, 从而使得修正值与原值重合.
2. 动量梯度下降(Momentum)
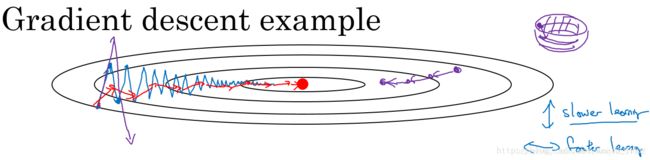
梯度下降如上图蓝线所示,梯度下降过程中有纵向波动,由于这种波动的存在,我们只能采取较小的学习率,否则波动会更大。
而使用动量梯度下降法(指数加权平均)后,经过平均,相当于抵消了上下波动,使波动趋近于零(如图中红线所示),这样就可以采用稍微大点的学习率加快梯度下降的速度。
算法实现
v d W = β v d W + ( 1 − β ) d W v_{dW} = \beta v_{dW} + (1-\beta)dW vdW=βvdW+(1−β)dW W : = W − α v d W W := W - \alpha v_{dW} W:=W−αvdW v d b = β v d b + ( 1 − β ) d b v_{db} = \beta v_{db} + (1-\beta)db vdb=βvdb+(1−β)db b : = b − α v d b b := b - \alpha v_{db} b:=b−αvdb
3. RMSprop(root mean square prop)
另一种加快梯度下降的算法, 调整更新参数时的步伐大小, 在变化剧烈的方向上步伐会比较小, 在变化平缓的方向上步伐较大, 因此学习率可以设置比较大.
S d W = β 2 S d W + ( 1 − β 2 ) d W 2 S_{dW} = \beta_2 S_{dW} + (1-\beta_2) dW^2 SdW=β2SdW+(1−β2)dW2 W : = W − α d W S d W + ϵ W := W - \alpha \frac{dW}{\sqrt{S_{dW}} + \epsilon} W:=W−αSdW+ϵdW S d b = β 2 S d b + ( 1 − β 2 ) d b 2 S_{db} = \beta_2 S_{db} + (1-\beta_2) db^2 Sdb=β2Sdb+(1−β2)db2 b : = b − α d b S d b + ϵ b := b - \alpha \frac{db}{\sqrt{S_{db}} + \epsilon} b:=b−αSdb+ϵdb
- RMSprop的原理是对 d W 2 dW^2 dW2和 d b 2 db^2 db2做加权移动平均, 假设纵轴方向为 b b b, 横轴方向为 W W W, 可以发现 d b db db变化剧烈, d W dW dW平缓, 因此 d W 2 dW^2 dW2的加权平均就会较小, d b 2 db^2 db2的加权平均较大, 对应的 S d W S_{dW} SdW的值就较小, S d b S_{db} Sdb的值较大.
- 为了与 Momentum 的参数 β ( β 1 ) \beta(\beta_1) β(β1)相区分,这里使用 β 2 \beta_2 β2
- ϵ \epsilon ϵ是为了防止除数为0, 一般 ϵ = 1 0 − 8 \epsilon = 10^{-8} ϵ=10−8
4. Adam优化算法(Adaptive moment estimation)
Adam 是 Momentum 和 RMSprop 的结合
算法实现:
i n i t i a l i z a t i o n : V d W = 0 , V d b = 0 , S d W = 0 , S d b = 0 initialization: V_{dW} = 0, V_{db} = 0, S_{dW} = 0, S_{db} = 0 initialization:VdW=0,Vdb=0,SdW=0,Sdb=0 v d W = β 1 v d W + ( 1 − β 1 ) d W v_{dW} = \beta_1 v_{dW} + (1-\beta_1)dW vdW=β1vdW+(1−β1)dW v d b = β 1 v d b + ( 1 − β 1 ) d b v_{db} = \beta_1 v_{db} + (1-\beta_1)db vdb=β1vdb+(1−β1)db v d W c o r r e c t e d = v d W 1 − β 1 t v_{dW}^{corrected} = \frac{v_{dW}}{1-\beta_1^t} vdWcorrected=1−β1tvdW v d b c o r r e c t e d = v d b 1 − β 1 t v_{db}^{corrected} = \frac{v_{db}}{1-\beta_1^t} vdbcorrected=1−β1tvdb S d W = β 2 S d W + ( 1 − β 2 ) d W 2 S_{dW} = \beta_2 S_{dW} + (1-\beta_2) dW^2 SdW=β2SdW+(1−β2)dW2 S d b = β 2 S d b + ( 1 − β 2 ) d b 2 S_{db} = \beta_2 S_{db} + (1-\beta_2) db^2 Sdb=β2Sdb+(1−β2)db2 S d W c o r r e c t e d = S d W 1 − β 2 t S_{dW}^{corrected} = \frac{S_{dW}}{1-\beta_2^t} SdWcorrected=1−β2tSdW S d b c o r r e c t e d = S d b 1 − β 2 t S_{db}^{corrected} = \frac{S_{db}}{1-\beta_2^t} Sdbcorrected=1−β2tSdb W : = W − α V d W c o r r e c t e d S d W c o r r e c t e d + ϵ W := W - \alpha \frac{V_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}} + \epsilon} W:=W−αSdWcorrected+ϵVdWcorrected b : = b − α V d b c o r r e c t e d S d b c o r r e c t e d + ϵ b := b - \alpha \frac{V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}} + \epsilon} b:=b−αSdbcorrected+ϵVdbcorrected
超参的选择
- α \alpha α: 需要调试
- β 1 \beta_1 β1: 推荐0.9, d W dW dW的加权平均
- β 2 \beta_2 β2: 推荐0.999, d W 2 dW^2 dW2的加权平均
- ϵ \epsilon ϵ: 推荐 1 0 − 8 10^{-8} 10−8
5. 学习率衰减
如果设置一个固定的学习率LR, 值较大的话, 很难收敛, 最后会在最低点附近波动; 值较小的话, 起初下降太慢. 因此, 为了下降快, 一开始学习率可以比较大; 为了能收敛, 学习率应该逐渐变小, 这就是学习率衰减
常用实现:
α = 1 1 + d e c a y _ r a t e ∗ e p o c h _ n u m α 0 \alpha = \frac{1}{1+ decay\_rate * epoch\_num}\alpha_0 α=1+decay_rate∗epoch_num1α0 α = 0.9 5 e p o c h _ n u m α 0 \alpha = 0.95^{epoch\_num}\alpha_0 α=0.95epoch_numα0 α = k e p o c h _ n u m α 0 \alpha = \frac{k}{epoch\_num}\alpha_0 α=epoch_numkα0
或者固定几个epoch之后, 衰减为原来的0.1(指数级衰减)