机器学习之回归算法(线性回归推导和实战)
1、主要回归算法
2、什么是回归算法
3、线性回归推导
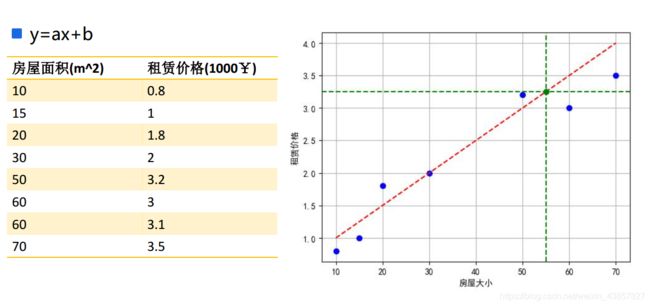
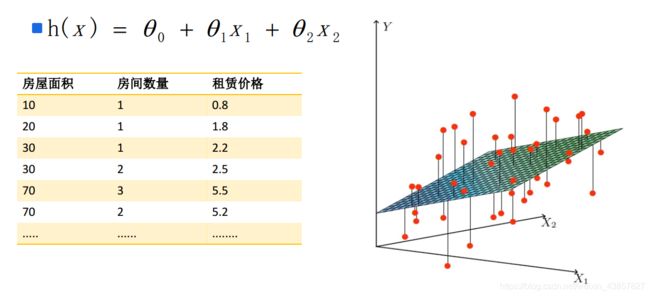


参考
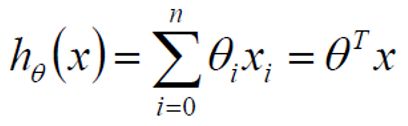
其中n为特征值的个数
误差
众所周知,当我们吧数据进行拟合后,不可能所有的数据均落在拟合线或者拟合平面内,因此拟合值跟实际值之间肯定会产生一个误差(我们用ε来表示误差),因此对于每个样本点来说:

一般来说误差具有独立同分布的特点,并且符合正态分布,其均值为0,方差为θ的平方:
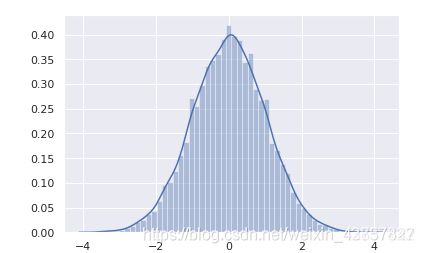
由于误差服从正态分布:
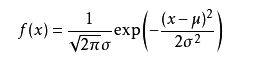
我们将误差函数与正态分布的公式组合(其中μ为0 ):
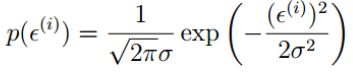
将误差公式代入上述式子中:

在这里我们引入似然函数,似然函数在统计学中扮演着重要的角色,我们可以简单理解为什么样的参数跟我们的数据组合后恰好是真实值:
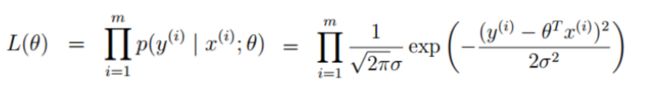
因为这个函数是一个累乘的式子,为了方便计算,我们将其取对数,将乘法变成加法,即为对数似然:
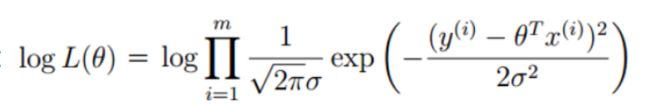
将式子展开化简:
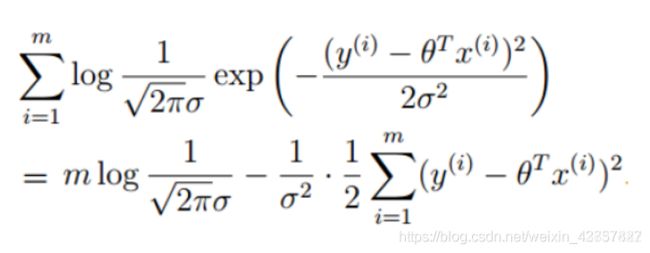
根据概率和统计中所学的知识,我们知道,对同一个似然函数,如果存在一个参数值,使得它的函数值达到最大的话,那么这个值就是最为“合理”的参数值。 化简后减数和被减数均为正数,要使函数获得最大值,那么我们就要使减数越小越好:

此时我们要求的就是J(θ)的极小值:
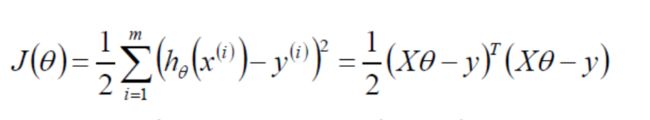
因为这个函数本质上来说是一个面,因此它的极值一般会出现在偏导为0的地方,于是我们对J(θ)分别对x和y求偏导:

如果偏导为0,则:
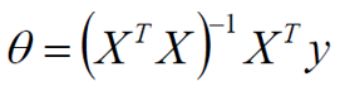
评估方法
我们最常用的评估方法为:

其取值越接近于1,我们认为模型的拟合程度越好。
先用最大似然函数求出目标函数,然后利用对目标函数利用最小二乘法求出参数
4、案例1:预测家庭用电(时间和电压的关系)
思路:
将时间划分为6个特征X,预测电压Y,设置回归函数为:![]()
目标:求参数θ
导包
#导包
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import time
import sklearn
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression #底层为最小二乘的线性包
from sklearn.preprocessing import StandardScaler # 标准化
from sklearn.metrics import mean_absolute_error,r2_score #评估标准
加载数据
# 加载数据
path='C:/Users/hubert/Desktop/Python零基础人工智能就业25G视频教程/5、机器学习/data/household_power_consumption_1000.txt' ## 1000行数据
'''
pandas读取csv文件默认是按块读取的,即不一次性全部读取;
另外pandas对数据的类型是完全靠猜的,所以pandas每读取一块数据就对csv字段的数据类型进行猜一次,
所以有可能pandas在读取不同块时对同一字段的数据类型猜测结果不一致。
low_memory=False 参数设置后,pandas会一次性读取csv中的所有数据,
然后对字段的数据类型进行唯一的一次猜测。这样就不会导致同一字段的Mixed types问题了。
'''
df = pd.read_csv(path, sep=';', low_memory=False) #当文件中的数据类型为单一类型时,low_memory能提高效率
# 异常数据处理(异常数据过滤)
new_df = df.replace('?', np.nan) #用nan替换 有问题的数据,方便进行dropna操作
datas = new_df.dropna(axis=0,how = 'any') # any只要该行有数据为nan,就进行删除操作;all是全为nan时才删除行
展示
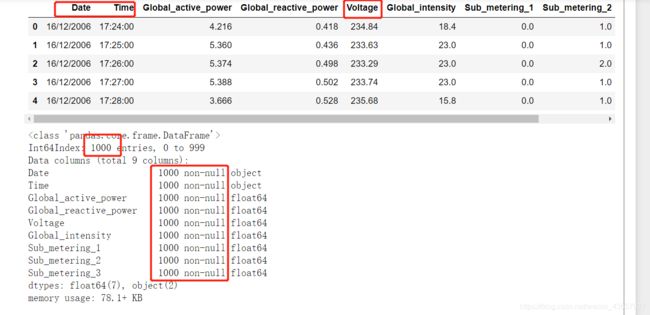
display(datas.head(5))
display(datas.info())
# 提取特征数据
## 创建一个时间字符串格式化字符串
def date_format(dt):
#dt在这里是一行,是Series类型,这一行有两个数据
#接下来要把这两个数据拼成字符串,再提取其中的‘年月日时分秒’
import time
t = time.strptime(' '.join(dt), '%d/%m/%Y %H:%M:%S') #函数根据指定的格式把一个时间字符串解析为时间元组。
return pd.Series([t.tm_year, t.tm_mon, t.tm_mday, t.tm_hour, t.tm_min, t.tm_sec])
## 时间和电压之间的关系(Linear)
# 获取x和y变量, 并将时间转换为数值型连续变量
X = datas.iloc[:,0:2] # 选取datas中前三列
X = X.apply(date_format, axis=1) #1代表按行,默认的是0代表列
Y = datas['Voltage']
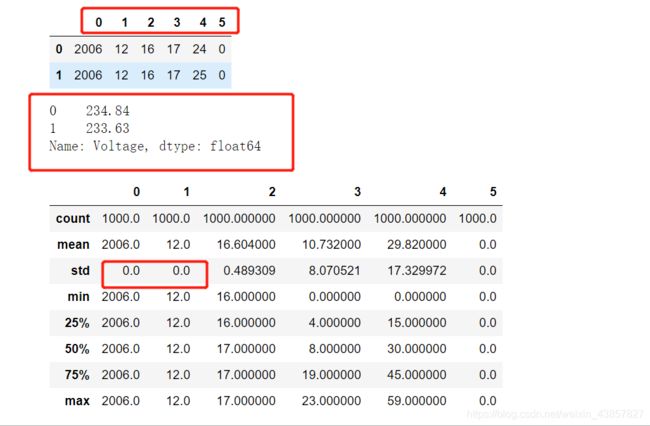
display(X.head(2))
display(Y.head(2))
display(X.describe())
# 划分数据集,标准化,模型训练,并使用模型预测
# 对数据集进行测试集和训练集划分
X_train,X_test,Y_train,Y_test = train_test_split(X, Y, test_size=0.2, random_state=0) # 训练集80%
# 数据标准化,必须先fit_transform(X_train),然后transform(X_test),保证归一化标准一样
# fit,训练模型,没有返回值
#transform,对数据进行转化
#fit_transform,先训练,再转换
ss = StandardScaler()
X_train = ss.fit_transform(X_train) # 对训练集进行训练并标准化
X_test = ss.transform(X_test) #在训练集的fit标准下,用X_test进行的标准化模型训练,用训练好的模型,再对X_test进行转换
# 模型训练
lr = LinearRegression()
lr.fit(X_train, Y_train) ## 训练模型
# 模型校验
y_pred = lr.predict(X_test) ## 预测结果
评估
# 模型效果(R^2)
#第一种方式,用lr.score
print("训练集R^2:",lr.score(X_train, Y_train)) #测训练集准确率
print("测试集R^2:",lr.score(X_test, Y_test)) #测试集准确率
#第二种方式,用metrics里的r2_score
print('测试集R^2:',r2_score(Y_test,y_pred))
#测试集均方误差MAE
print('测试集均方误差:',mean_absolute_error(Y_test,y_pred))
#测试集平均方差MSE和RMSE
MSE=np.average((y_pred-Y_test)**2)
RMSE=np.sqrt(MSE)
print("MSE:",MSE)
print("RMSE:",RMSE)
## 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False
## 预测值和实际值画图比较
t=np.arange(len(X_test)) #用测试集数据量200作为横轴
plt.figure(facecolor='w') # 背景颜色白色
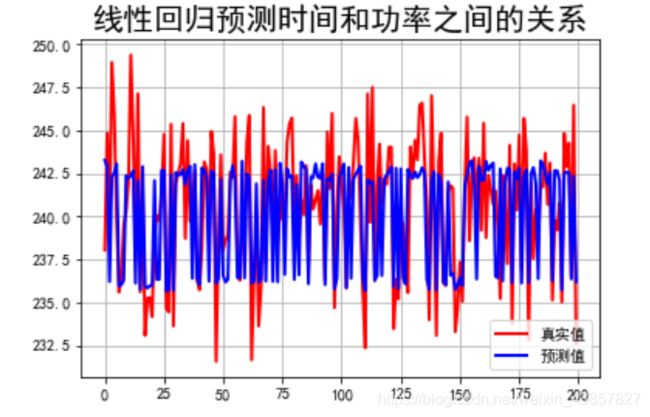
plt.plot(t, Y_test, 'r-', linewidth=2, label=u'真实值')
plt.plot(t, y_pred, 'b-', linewidth=2, label=u'预测值')
plt.legend(loc = 'lower right')
plt.title(u"线性回归预测时间和功率之间的关系", fontsize=20)
plt.grid(b=True)#网格
plt.show()
#打印参数y=239.92665+0*x1+0*x2+3.97781449*x3+0.87333465*x4+0.17064799*x5+0*x6
print(lr.coef_) #打印参数项
print(lr.intercept_) #打印截距项
5、案例5:预测家庭用电(电流和功率的关系)
不利用线性回归模块,直接用上面推导的
求出每个特征的参数,特征X为功率两个,电压Y为一个,该方法没有考虑截距,得到y=θ1*x+θ2*x
导包读数据
#导包
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import time
import sklearn
from sklearn.model_selection import train_test_split
## 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False
# 加载数据
path='C:/Users/hubert/Desktop/Python零基础人工智能就业25G视频教程/5、机器学习/data/household_power_consumption_1000.txt' ## 1000行数据
df = pd.read_csv(path, sep=';', low_memory=False) #当文件中的数据类型为单一类型时,low_memory能提高效率
df.head(2)
## 功率和电流的关系
X=df.iloc[:,2:4]
Y=df.iloc[:,5]
display(X.head(2))
display(Y.head(2))
# 对数据集进行测试集和训练集划分
X_train,X_test,Y_train,Y_test = train_test_split(X, Y, test_size=0.2, random_state=0) # 训练集80%
最小二乘法需要是矩阵,但是dataframe不是矩阵
# 最小二乘法需要是矩阵,但是dataframe不是矩阵
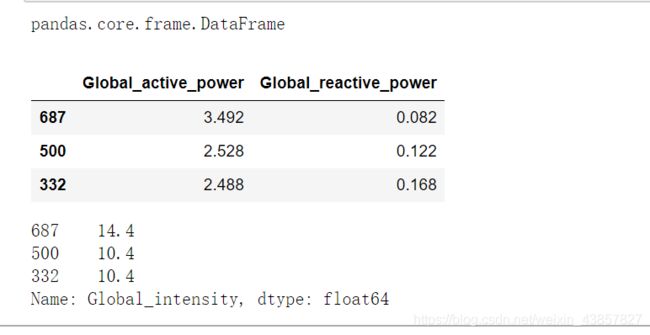
display(type(X_train))
display(X_train.head(3))
display(Y_train.head(3))
# 将X和Y转换成矩阵
X_train1=np.mat(X_train) # X_train1:800*2
display(type(X_train1))
Y_train1=np.mat(Y_train) # Y_train1:800*1
display(type(Y_train1))
# X*Y,需要维数对应,所以把Y转置
Y_train1=Y_train1.reshape(-1,1)
计算 θ = ( X T X ) − 1 ( X T X ) θ=(X^TX)^{-1}(X^TX) θ=(XTX)−1(XTX)
Theta=(X_train1.T*X_train1).I*X_train1.T*Y_train1
print(Theta)
# 对测试集进行预测y=Theta*x
X_test1=np.mat(X_test)
y_pre = X_test1*Theta
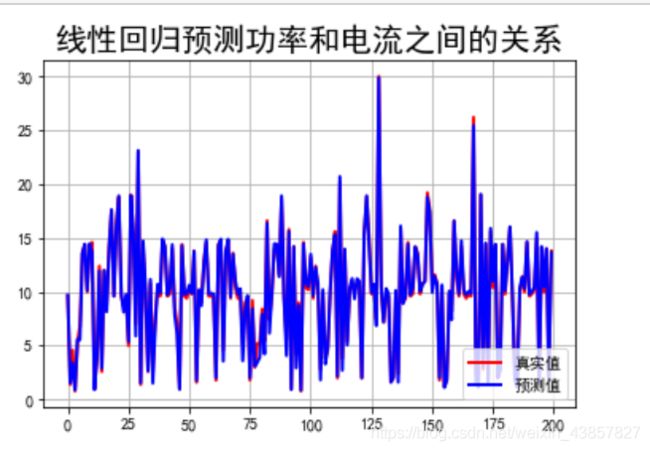
可视化
# 可视化
t=np.arange(len(X_test1)) #用测试集数据量200作为横轴
plt.figure(facecolor='w') # 背景颜色白色
plt.plot(t, Y_test, 'r-', linewidth=2, label=u'真实值')
plt.plot(t, y_pre, 'b-', linewidth=2, label=u'预测值')
plt.legend(loc = 'lower right')
plt.title(u"线性回归预测功率和电流之间的关系", fontsize=20)
plt.grid(b=True)#网格
plt.show()
6、模型保存
import sklearn
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler # 标准化
ss = StandardScaler()
lr = LinearRegression()
# 模型保持/持久化
# 在机器学习部署的时候,实际上其中一种方式就是将模型进行输出;
# 另一种方式就是直接将预测结果进行输出。
# 模型输出一般是将模型直接输出到磁盘文件。
from sklearn.externals import joblib
# 保存文件要求指定的文件夹存在,默认是当前路径
joblib.dump(ss,'data_ss.model') # 保存标准化模型
joblib.dump(lr,'data_lr.model') # 保存线性模型
# 加载模型
ss1 = joblib.load('data_ss.model') # 加载模型
lr1 = joblib.load('data_lr.model')
# 用模型进行预测
data1=[[2006,12,17,12,25,0]]
data2=[[2006,12,1,17,24,0]]
data11=[234.84]
data22=[233.63]
data1=ss1.fit_transform(data1)
data2=ss1.transform(data2)
lr1.fit(data1, data11) ## 训练模型
y_pred = lr1.predict(data2) ## 预测结果
print([data22,y_pred])