二叉排序树（Binary Sort Tree，二叉查找树，二叉搜索树）--【算法导论】

今天的收获就是二叉搜索树，“好记性不如烂笔头”，写下来加深一下印象；

1、首先是了解了二叉搜索树（Binary Sort Tree）又称二叉查找树，亦称二叉排序树。 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉搜索树。

2、接下来看的是查询二叉搜索树，查询二叉搜索树的内容比较多；

（1）查找：即是查询关键字，若存在，返回该节点的指针；否则，返回空；这个书中给了两段伪码，迭代、递归随意；

（2）最大关键字及最小关键字元素：顾名思义，肯定是二叉搜索树的最大最小值，以最大关键字为例，一直查询树的右孩子，直到改节点无右孩子为止，该节点就是最大关键字，当然，最小关键字同理；

（3）后继与前驱：对一个节点来说，最大的小于该节点值的即是前驱，最小的大于该节点值的即是后继。以后继为例，如果该节点的右子树不为空，那么后继就是右子树中最小关键字元素；若是该节点右孩子不存在，这时，只需由该节点往上寻找，直到这个节点是其父节点的左孩子即可。当然，前驱也是类似情况；

3、然后看的是插入与删除，这一节也挺关键的；

（1）插入：插入我们都知道，建立的二叉搜索树就是一个节点一个节点的进行插入的。遍历该树，找到适合的位置，就将节点插入了；

（2）删除：这个就比较复杂了，考虑的情况比较多；

一：该节点是叶子节点，这个删除是最简单的，将其改为空，并修改父节点即可；

二：该节点只有一个孩子（左孩子或右孩子，这个在具体实现时不同操作），这时只要将该节点的孩子节点放在该节点上，同时修改该节点的父节点即可；

三：该节点有两个孩子，这个是最复杂的，不过由于后来没思路，编代码的时候参考一位仁兄，他的思想是直接找到该节点的后继节点，将其删除（这个后继节点一定是存在的，因为它有两个孩子啊，至少右孩子就比它大，故而存在），然后将该节点的值改为后继节点的值即可（当然提前把后继的值留下...）

4、最后看的是随机构建二叉搜索树，貌似这样二叉树的高度比较理想，平均深度是lgn，不会发生“过激”的情况。

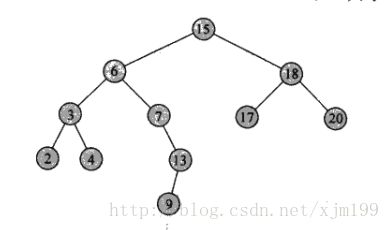
如上时间复杂度皆为O(h)，这一章是《算法导论》的内容，书中写得还是比较详细的，伪码也给了不少，建的二叉搜索树如下；

    ElemType nodeArray[11] = {15, 6, 18, 3, 7, 17, 20, 2, 4, 13, 9};  //二叉数
    Create(root, nodeArray, 11);  //创建二叉搜索数

    cout<<"该节点的值"<key<right->right)->key<left->right->right)->key<key<right->right)->key<left->right->left)->key<

进行如上操作，创建二叉搜索树就不多说了，另外如查找关键字返回该指针也是直接使用，并未判断，在实际程序中需要写出，如上只是简单测试一下；

首先是cout<<"该节点的值"<key<输入关键字15这个节点的值，即15；

接下来cout<<"min = "<key<root->right->right的值20，故而它的前驱cout<<"前驱"<right->right)->key<是18；

root->left->right->right是13，故而它的后继是cout<<"后继"<left->right->right)->key<  是15；

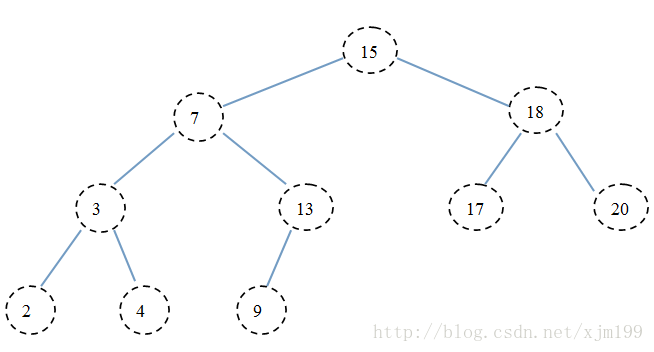
这时删除节点值为6的节点DeleteNode(root, 6);成了一个新的二叉搜索树；

按照之前删除的思想，因为删除的是节点6，它的后继是7，这时删除7，此时是第二种情况，直接将13，9移上来，将6改为7；

这时cout<<"该节点的值"<key<依然是15；

最大最小也依然没变，cout<<"min = "<key<root->left的值是7，它的前驱cout<<"前驱"<left)->key<是4；
root->left->right->left是9，它的后继cout<<"后继"<left->right->left)->key<是13；

运行如下：

大致就是这样的，代码如下（补丁不少）：

#include 
#include 
#include 

using namespace std;
typedef int ElemType;
typedef struct Node
{
    ElemType key;        //关键字
    struct Node *left;   //左孩子
    struct Node *right;  //右孩子
    struct Node *parent; //父节点
} Node, *PNode;

//插入
void Insert(PNode &root, ElemType key)
{
    //初始化b被插入结点
    PNode p=(PNode)malloc(sizeof(Node));
    p->key = key;
    p->left = NULL;
    p->right = NULL;
    p->parent = NULL;
    //空树
    if(root == NULL)
    {
        root = p;
        return;
    }
    //左孩子
    if(root->left == NULL && root->key > key)
    {
        p->parent = root;
        root->left = p;
        return;
    }
    //右孩子
    if(root->right == NULL && root->key < key)
    {
        p->parent = root;
        root->right = p;
        return;
    }

    //关键值小于此时的节点值，放在左树
    //准备改回迭代的，今晚没成功...
    if(key < root->key)
        Insert(root->left,key);
    else
        Insert(root->right,key);
}

//查找元素,找到返回关键字的结点指针，没找到返回NULL
PNode Search(PNode root, ElemType key)
{
    if(root == NULL || root->key == key)
        return root;

    if(key < root->key) //查找左子树
        return Search(root->left,key);
    else //查找右子树
        return Search(root->right,key);
}

//查找最小关键字,空树时返回NULL
PNode SearchMin(PNode root)
{
    if(root == NULL)
        return root;

    while(root->left != NULL)
        root = root->left;
    return root;
}

//查找最大关键字,空树时返回NULL
PNode SearchMax(PNode root)
{
    if(root == NULL)
        return root;

    while(root->right != NULL) //迭代
        root = root->right;
    return root;
}

//查找前驱
PNode SearchPredecessor(PNode x)
{
    if(x == NULL)  //空
        return x;

    //若存在左孩子，前驱是其左子树中最大的
    if(x->left != NULL)
        return SearchMax(x->left);

    PNode y = x->parent;
    while(y != NULL && x == y->left)
    {
        x = y;
        y = x->parent;
    }
    return y;
}

//查找后继
PNode SearchSuccessor(PNode x)
{
    if(x == NULL)  //空
        return x;

    //若存在右孩子，后继是其右子树中最小的
    if(x->right != NULL)
        return SearchMin(x->right);

    PNode y = x->parent;
    while(y != NULL && x == y->right)
    {
        x = y;
        y = x->parent;
    }
    return y;
}

int DeleteNode(PNode &root,ElemType key)
{
    PNode q;
    //查找到要删除的结点
    PNode p = Search(root, key);

    //没查到此关键字
    if(p == NULL)
        return 0;
    //一共有四种情况，该节点是叶子节点、只有左孩子、只有右孩子、左右孩子都有
    //叶子结点
    if(p->left == NULL && p->right == NULL)
    {
        //只有根节点
        if(p->parent == NULL)
        {
            free(p);
            root = NULL;
        }
        else
        {
            //删除的结点是左孩子
            if(p->parent->left == p)
                p->parent->left = NULL;
            else
                p->parent->right = NULL;
            free(p);
        }
    }

    //左孩子
    else if(p->left != NULL && p->right == NULL)
    {
        p->left->parent = p->parent;
        //如果删除是根结点
        if(p->parent == NULL)
            root = p->left;
        //父节点的左孩子
        else if(p->parent->left == p)
            p->parent->left = p->left;
        else
            p->parent->right = p->left;
        free(p);
    }
    //右孩子
    else if(p->right != NULL && p->left == NULL)
    {
        p->right->parent = p->parent;
        //如果删除是根结点
        if(p->parent == NULL)
            root = p->right;
        //是父节点的左孩子
        else if(p->parent->left == p)
            p->parent->left=p->right;
        else
            p->parent->right=p->right;
        free(p);
    }
    //左右孩子都有
    //该结点的后继结点肯定无左子树
    //删掉后继结点,后继结点的值代替该结点
    else
    {
        //找到要删除结点的后继
        q = SearchSuccessor(p);
        ElemType temp = q->key;    //暂存后继结点的值

        //删除后继结点
        DeleteNode(root, q->key);
        p->key = temp;
    }
    return 1;
}

//创建树
void Create(PNode& root, ElemType *keyArray, int length)
{
    for(int i = 0; i < length; i++)
        Insert(root, keyArray[i]);  //插入
}

int main()
{
    PNode root = NULL;
    ElemType nodeArray[11] = {15, 6, 18, 3, 7, 17, 20, 2, 4, 13, 9};  //二叉数
    Create(root, nodeArray, 11);  //创建二叉搜索数

    cout<<"该节点的值"<key<right->right)->key<left->right->right)->key<key<left)->key<left->right->left)->key<

o(∩_∩)o