Armstrong基础拓扑学读书笔记——第二章:连续性
2.1 开集和闭集
拓扑空间
(定义2.1) X X X是一个拓扑空间,如果它存在一组非空子集(称为开集)族,满足
- 无限个开集的并是开集
- 有限个开集的交是开集
- 全集和空集是开集
无限开集是不是开集的例子。
设 X X X是定义在 R 2 R^2 R2上的欧式拓扑,开集取常规定义下的开圆,取其中无数个开集
( x , y ) ∣ x 2 + y 2 < 1 n , n = 1 , 2 , ⋯ {(x,y)|x^2+y^2<\frac{1}{n}}, n=1,2,\cdots (x,y)∣x2+y2<n1,n=1,2,⋯。
显然这无限个开集的交是原点,而原点不是开集。
邻域
对拓扑空间 X X X中的一个点(元素) p p p,任何一个包含 p p p的开集都是 p p p的一个邻域。
子空间诱导的拓扑
X X X是一个拓扑空间(背景集合和开集族), Y Y Y是 X X X上(背景集合)的一个子集,若定义 Y Y Y中的开集为 X X X中开集和 Y Y Y的交,则 Y Y Y为 X X X在子空间上诱导(induce)的拓扑。
离散拓扑
X X X中所有的子集均为开集构成的拓扑空集。
闭集
X X X是一个拓扑空间, X X X的一个子集称为一个闭集,如果这个子集的补为开集。
一个子集可以同时为开集和闭集。比如在 X = { 0 , 1 } X=\{0,1\} X={ 0,1}上赋予离散拓扑,则由定义, { 0 } \{0\} { 0}和 { 1 } \{1\} { 1}显然同时为开集和闭集。
极限点
A A A是拓扑空间 X X X的一个子集。一个点(元素) p ∈ X p \in X p∈X被称为 A A A的极限点,当且仅当对于任意 p p p的邻域,均包含至少一个点,它属于 A − { p } A-\{p\} A−{ p}。
例1: X X X是定义在 R 1 R^1 R1上的欧式拓扑, A A A取所有 1 / n , n = 1 , 2 , ⋯ 1/n, n=1,2,\cdots 1/n,n=1,2,⋯点组成的点集,则 A A A中唯一的极限点是原点。
例2: X X X是定义在 R 1 R^1 R1上的欧式拓扑, A A A取 [ 0 , 1 ) [0,1) [0,1),则 A A A中任一点均为极限点,且1也是一个 A A A的极限点。
例3: X X X是定义在 R 3 R^3 R3上的欧式拓扑, A A A取 R 3 R^3 R3中所有的有理点,则 X X X全体都是极限点。
例4: X X X是定义在 R 3 R^3 R3上的欧式拓扑, A A A取 R 3 R^3 R3中所有的整数点,则 A A A没有极限点。
闭集和极限点的定理
(定理2.2) 一个集合是闭集,当且仅当它包含了它自身所有的极限点。
闭集和闭包的关系
(定理2.3) 子集 A A A的闭包为包含 A A A的最小闭集,或者说,子集 A A A的闭包为所有包含 A A A的闭集的交。
(推论2.4) 一个子集为闭集,当且仅当它的闭包为自身。
集合 A A A的闭包写作 A ˉ \bar{A} Aˉ。
稠密
如果一个子集的闭包为整个拓扑空间,则称这个子集是稠密的。
如上述例3中 R 3 R^3 R3上所有的有理点的集合是稠密的。
稠密集和空间中任意一个开集相交。
内部点(集)
子集 A A A的内部点(interior),通常写作 A ˚ \mathring{A} A˚,指所有包含 A A A的集合的交。
一个点 x x x属于集合 A A A的内部点,当且仅当集合 A A A是点 x x x的邻域。
开集的内部点集就是开集本身。
边界点(集)
拓扑空间 X X X中的子集 A A A的边界点(frontier)定义为 A A A的闭包和 X − A X-A X−A的闭包的交。
一个等价的定义为 X X X减去 A A A的内部点,再减去 X − A X-A X−A的内部点。
拓扑基
如果有一个拓扑空间 X X X,以及一组 X X X中的开集 β \beta β,如果 X X X中任何一个开集都可以表示成若干个 β \beta β中开集的并,则 β \beta β构成 X X X中的一个拓扑基。
一个等价的定义是,对于任何一个点 x x x,取它的邻域 N N N, N N N中总有一个点,这个点属于 β \beta β中某一个开集。
例:对于 R 2 R^2 R2上的欧式拓扑,开圆盘是其中一个拓扑基,开矩形也是其中的一个拓扑基。
(定理2.5) 设 β \beta β是集合 X X X中的一个子集族,若有限个 β \beta β中的集合相交仍在 β \beta β中,且 ⋃ β = X \bigcup \beta = X ⋃β=X,则 β \beta β为 X X X的一个拓扑基,形成 X X X的拓扑空间。
证明:取开集族为所有 β \beta β中集合并成的集合,验证这样的开集族满足拓扑空间的三个条件即可。按开集族的取法,无限并在开集族中;按定理的条件,有限交在开集族中;按定理的条件,全集在开集族中;人工添加空集到开集族中。显然赋予这样开集族的 X X X是拓扑空间。得证。
2.2 连续函数
连续函数
(定理2.6) 拓扑空间 X X X到拓扑空间 Y Y Y的函数是连续的(continuous),当且仅当 Y Y Y中开集的原像(inverse image)在 X X X中是开集。
映射
连续函数通常被称为映射(map)。
(定理2.7) 映射的复合还是映射。即 f : X → Y f: X \rightarrow Y f:X→Y是连续函数, g : Y → Z g: Y \rightarrow Z g:Y→Z是连续函数,则 f ∘ g : X → Z f \circ g: X \rightarrow Z f∘g:X→Z也是连续函数。
子空间诱导拓扑下的连续函数
(定理2.8) 设 f : X → Y f: X \rightarrow Y f:X→Y是连续函数, A A A是 X X X的子集,且赋予子空间诱导的拓扑,则 f ∣ A : A → Y f|A: A \rightarrow Y f∣A:A→Y也是连续函数。
连续函数的性质
(定理2.9) 以下5个命题等价:
(a). f : X → Y f: X \rightarrow Y f:X→Y连续
(b). β \beta β是 Y Y Y的一个拓扑基,任何一个 β \beta β中的集合的原像是 X X X中的开集
©. ∀ A ⊆ X , f ( A ˉ ) ⊆ f ( A ) ‾ \forall A \subseteq X, f(\bar{A}) \subseteq \overline{f(A)} ∀A⊆X,f(Aˉ)⊆f(A)
(d). ∀ B ⊆ Y , f − 1 ( B ) ‾ ⊆ f − 1 ( B ˉ ) \forall B \subseteq Y, \overline{f^{-1}(B)} \subseteq f^{-1}(\bar{B}) ∀B⊆Y,f−1(B)⊆f−1(Bˉ)
(e). Y Y Y中闭集的原像都是 X X X中的闭集。
证明:证明命题等价的方法为 ( a ) ⇒ ( b ) ⇒ ( c ) ⇒ ( d ) ⇒ ( e ) ⇒ ( a ) (a) \Rightarrow (b) \Rightarrow (c) \Rightarrow (d) \Rightarrow (e) \Rightarrow (a) (a)⇒(b)⇒(c)⇒(d)⇒(e)⇒(a)。
( a ) ⇒ ( b ) (a) \Rightarrow (b) (a)⇒(b),由定义显然。
( b ) ⇒ ( c ) (b) \Rightarrow (c) (b)⇒(c),在 A ˉ \bar{A} Aˉ中任取一点 x x x,若 x ∈ A x \in A x∈A,则显然 f ( x ) ∈ f ( A ) ⊆ f ( A ) ‾ f(x) \in f(A) \subseteq \overline{f(A)} f(x)∈f(A)⊆f(A);若 x ∉ A x \notin A x∈/A,则 x x x是 A A A的一个极限点。因此,我们只需要证明 x x x是 A A A的一个极限点时, f ( x ) f(x) f(x)是 f ( A ) f(A) f(A)的极限点的情况。任取 f ( x ) f(x) f(x)的一个邻域 N N N,由(b),可取 Y Y Y中一个拓扑基 B ∈ β B \in \beta B∈β,使得 f ( x ) ∈ B ⊆ N f(x) \in B \subseteq N f(x)∈B⊆N。要证 f ( x ) f(x) f(x)是 f ( A ) f(A) f(A)的极限点,即证存在一点 f ( x ′ ) f(x') f(x′), f ( x ′ ) ∈ N f(x') \in N f(x′)∈N且 f ( x ′ ) ∈ f ( A ) f(x') \in f(A) f(x′)∈f(A)。由(b), f − 1 ( B ) f^{-1}(B) f−1(B)是 X X X中的开集,因为 x ∈ f − 1 ( B ) x \in f^{-1}(B) x∈f−1(B)且 x x x为极限点,故存在一点 x ′ ∈ A x' \in A x′∈A且 x ′ ∈ f − 1 ( B ) x' \in f^{-1}(B) x′∈f−1(B)。因此显然, f ( x ′ ) ∈ f ( A ) f(x') \in f(A) f(x′)∈f(A)且 f ( x ′ ) ∈ B ⊆ N f(x') \in B \subseteq N f(x′)∈B⊆N。命题得证。
( c ) ⇒ ( d ) (c) \Rightarrow (d) (c)⇒(d), ∀ B ⊆ Y \forall B \subseteq Y ∀B⊆Y, ∃ A ⊆ X \exist A \subseteq X ∃A⊆X,使得 A = f − 1 ( B ) A = f^{-1}(B) A=f−1(B)。代入©,得到 f ( f − 1 ( B ) ‾ ) ⊆ f ( f − 1 ( B ) ) ‾ = B ˉ f(\overline{f^{-1}(B)}) \subseteq \overline{f(f^{-1}(B))} = \bar{B} f(f−1(B))⊆f(f−1(B))=Bˉ,两侧同时取 f − 1 f^{-1} f−1,则(d)得证。
( d ) ⇒ ( e ) (d) \Rightarrow (e) (d)⇒(e),如果 B B B是 Y Y Y中的闭集,则 B = B ˉ B=\bar{B} B=Bˉ。由(d), f − 1 ( B ) ‾ ⊆ f − 1 ( B ˉ ) = f − 1 ( B ) \overline{f^{-1}(B)} \subseteq f^{-1}(\bar{B}) = f^{-1}(B) f−1(B)⊆f−1(Bˉ)=f−1(B),因此(e)得证。
( e ) ⇒ ( a ) (e) \Rightarrow (a) (e)⇒(a),设 U U U是 Y Y Y中的开集,则 f − 1 ( U ) ⨿ f − 1 ( Y − U ) = X f^{-1}(U) \amalg f^{-1}(Y-U) = X f−1(U)⨿f−1(Y−U)=X,其中 ⨿ \amalg ⨿表示无交并。(这里等号成立,是因为函数的性质决定了 f f f和 f − 1 f^{-1} f−1为一一映射且为满射。)因为闭集的原像是闭集,且因为 Y − U Y-U Y−U是闭集,因此 f − 1 ( Y − U ) f^{-1}(Y-U) f−1(Y−U)是闭集。因此 f − 1 ( U ) = X − f − 1 ( Y − U ) f^{-1}(U) = X - f^{-1}(Y-U) f−1(U)=X−f−1(Y−U),因此开集的原像是开集。(a)得证。
连续函数的逆不一定为连续函数。
例: X X X为 [ 0 , 1 ) [0,1) [0,1)赋予 R 1 R^1 R1欧式拓扑的子空间拓扑, Y Y Y为单位圆赋予 R 2 R^2 R2欧式拓扑的子空间拓扑。 f : X → Y = e 2 π i x f:X \rightarrow Y = e^{2\pi ix} f:X→Y=e2πix为连续函数,因为任取 X X X上的开区间,都是 Y Y Y上的开曲线区间。但 f − 1 f^{-1} f−1不是连续函数,因为 Y Y Y中取跨越 ( 1 , 0 ) (1,0) (1,0)点的一段开曲线区间,对应于 X X X左右两侧一段开区间和一段闭区间。见图2.1。
同胚
如果存在 X X X到 Y Y Y上一一对应、满射且连续的函数,且其逆函数也连续,则 X X X和 Y Y Y同胚。
例:球极投影。去掉北极点的球和平面同胚。可构造从北极点向球面各点发射的射线,总是能和赤道平面相交在一点,它们显然一一对应、满射、连续、逆函数连续,因此同胚。
2.3 充满面的曲线
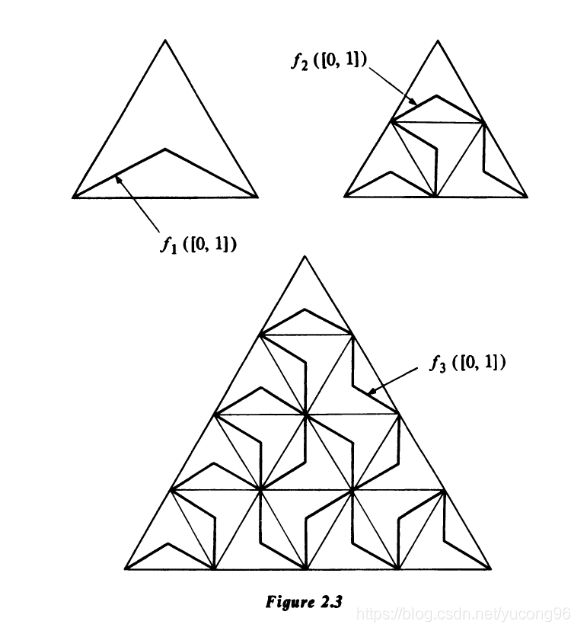
皮亚诺曲线
构造方法如图2.3所示。
可证明皮亚诺曲线充满了整个三角形。另外由于皮亚诺曲线是 [ 0 , 1 ] [0,1] [0,1]到整个面的连续映射,因此,单方向的连续映射不能推出同胚。
2.4 Tietze扩张定理
暂跳过
参考
- Basic Topology, M. A. Armstrong
- Bilibili基础拓扑学公开课