可解释的卷积滤波器 SincNet

可解释的卷积滤波器 SincNet

Ravanelli, M. 在 NIPS 2018 进一步讨论了 SincNet 可解释意义，令人感觉该模型已经能够胜任在说话人识别的基础上胜任更多的语音处理任务。因此，在先前的 SincNet 讲解基础上，笔者进一步分析 SincNet 的可解释性、相关的无监督方法和潜在的安全威胁。

Notes from Speaker Recognition from Raw Waveform with SincNet:

In particular, we propose SincNet, a novel Convolutional Neural Network (CNN) that encourages the first layer to discover more meaningful filters by exploiting parametrized sinc functions.

This inductive bias offers a very compact way to derive a customized filter-bank front-end, that only depends on some parameters with a clear physical meaning.

The proposed architecture converges faster, performs better, and is more interpretable than standard CNNs.

摘要

2018 年以后，SincNet 具有更快的收敛速度、更佳的表示能力和更好的可解释性，但也暴露出其对抗攻击的脆弱性。笔者详细分析 SincNet 四部分：设计原理、可解释性、无监督学习应用和对抗攻击。考虑到 SincNet 在频域方面的物理意义，它将为语音处理应用的研发提供极大的便利，例如说话人识别与语音识别。

SincNet 设计

在先前的 SincNet 讲解基础上，该部分着重分析参数化滤波器的设计，及其相关物理含义。值得重视的是：信号处理技术中的带通滤波器是启发 SincNet 设计的主要来源，因此，笔者从带通滤波器的角度来描述参数化滤波器的设计原理。

为了更好的理解参数化滤波器的设计原理，可以通过传统卷积函数中的一维卷积来看待该滤波器，例如 PyTorch 的 nn.Conv1d。在此基础上，可以任务该滤波器就是一个长度为 $L$ 的一维向量，这些向量的权重，可以通过参数更新的方法学习获得。

根据上图给出第一行图片，可以理解为三个不同的一维卷积 $c=\{c_i{\}}_{i=0}^{250}$，它们的长度都为 $L=251$。通过这样的数学符号，可以将其与二维卷积直接联系起来。简单来说，SincNet 带通滤波器就是一种特定的一维卷积。

那么如何设计这样一个特定的一维卷积函数呢？**直觉地，让滤波器去学习特定频域范围内的信息。**为设计这样的滤波器，需要了解一下内容：

1. 为什么希望 SincNet 参数化滤波器来学习特定频率范围的内容？

   • 问题：音调和基频是帮助识别说话人身份的重要线索，也是非常重要且具有物理含义的声学特性。Mel-Scale 滤波器组提供了提取这类信息类似的功能。然而，传统的频谱提取方法，例如 MFCC、PLP、FBANK 等，是依据以往经验提取的信号信息，无法直接证明这些信息的所有组成成分都是有利于特定语音处理任务的。
   • SincNet 参数化滤波器：为了适应特定的语音处理任务，设计可学习的滤波器，来替换人工提取的滤波器组或者频谱相关系数。因此，该学习滤波器满足一下设计要求：
     • 处理原始信号：在深度学习框架中，它位于与原始波形直接关联的位置，即网络第一层，替代 MFCC、FBANK 或者 PLP 的功能。
     • 提取频率相关的信息：频谱分析提供了非常重要的信息，例如音调和基频，或者特定频带的信息。
     • 要具有物理含义：“数字信号处理”从物理的角度提供了大量的数字信号滤波器设计相关的知识，例如高通滤波器、低通滤波器、带通滤波器等。

2. 为什么带通滤波器可以学习特定频率范围内的内容？

   • 带通滤波器：在“数字信号处理”领域，带通滤波器的属性是让特定频带（连续频率范围）的数字信号通过。上图的第二行描述了三种带通滤波器的频域特性——通带。它往往可以用于噪声过滤，例如高频噪声过滤。

   • 数字信号：在“数字信号处理”领域，有一个关于傅里叶的观点：**任何周期函数，都可以看作是不同振幅，不同相位正弦波的叠加。**就像在“高等数学”的范畴下，把一个周期函数展开成傅里叶级数。

     根据经验，把说话人的语音看作一个周期信号是可行的，

     或者说，忽略语音信号的非周期成分不会显著影响语音处理效果。

   • 通过与衰减：根据傅里叶理论，带通滤波器将通带以外的频率都衰减掉了，而留下的通带内的频率。

3. 如何设计这样的滤波器？

   • $c=\{c_i{\}}_{i=0}^{250}$：为了使一维卷积满足带通滤波器的特性，需要构建与两个截至频（低、高）相关的参数化模型。这里已知滤波器频域特性，可以通过逆向傅里叶变换来获得滤波器 $g(n,f_1,f_2)$ 在频域上的参数 ($f_1$ 与 $f_2$)，相应的数学公式为：

     $$g(n,f_1,f_2)=2f_2\text{sinc}(2\pi f_{2}n)-2f_1\text{sinc}(2\pi f_{1}n)$$

     其中 $n$ 表示滤波器长度 $L$，上图中，$n=L=251$。

   • 窗函数 (window)：带通滤波器的矩形窗特性无法通过有限的傅里叶成分精准的描述，且这样的矩形窗特性存在突变不连续性。为此，“数字信号处理”领域采用 window 来克服。

根据上述原理，带通滤波器的一维卷积提供了一种提取信号特定频率范围信息的功能，它的截至频的可学习的特性，使得该一维卷积可以通过数据来自适应地学到带通滤波器的通带。本质上，SincNet 的参数化滤波器是借鉴了带通滤波器的设计，并使其可学习化。

SincNet 中第一层滤波器，即参数话带通滤波器，其精简后的代码（完整代码参考链接）如下。特别地，SincNet 的输入语音通常采用 200 ms 长与 10 ms 间隔的采样方式。

class SincConv_fast(nn.Module):
    @staticmethod
    def to_mel(hz):
        return 2595 * np.log10(1 + hz / 700)

    @staticmethod
    def to_hz(mel):
        return 700 * (10 ** (mel / 2595) - 1)

    def __init__(self, out_channels, kernel_size, sample_rate=16000, in_channels=1,
                 stride=1, padding=0, dilation=1, bias=False, groups=1, min_low_hz=50, min_band_hz=50):
        super(SincConv_fast,self).__init__()
        self.out_channels = out_channels
        self.kernel_size = kernel_size
        # Forcing the filters to be odd (i.e, perfectly symmetrics)
        if kernel_size%2==0:
            self.kernel_size=self.kernel_size+1
        self.stride = stride
        self.padding = padding
        self.dilation = dilation
        self.sample_rate = sample_rate
        self.min_low_hz = min_low_hz
        self.min_band_hz = min_band_hz

        # initialize filterbanks such that they are equally spaced in Mel scale
        low_hz = 30
        high_hz = self.sample_rate / 2 - (self.min_low_hz + self.min_band_hz)

        mel = np.linspace(self.to_mel(low_hz),
                          self.to_mel(high_hz),
                          self.out_channels + 1)
        hz = self.to_hz(mel)
        
        # filter lower frequency (out_channels, 1)
        self.low_hz_ = nn.Parameter(torch.Tensor(hz[:-1]).view(-1, 1))

        # filter frequency band (out_channels, 1)
        self.band_hz_ = nn.Parameter(torch.Tensor(np.diff(hz)).view(-1, 1))

        # Hamming window
        # computing only half of the window
        n_lin=torch.linspace(0, (self.kernel_size/2)-1, steps=int((self.kernel_size/2))) 
        self.window_=0.54-0.46*torch.cos(2*math.pi*n_lin/self.kernel_size);

        # (1, kernel_size/2)
        n = (self.kernel_size - 1) / 2.0
        # Due to symmetry, I only need half of the time axes
        self.n_ = 2*math.pi*torch.arange(-n, 0).view(1, -1) / self.sample_rate 

    def forward(self, waveforms):
        self.n_ = self.n_.to(waveforms.device)
        self.window_ = self.window_.to(waveforms.device)
        low = self.min_low_hz  + torch.abs(self.low_hz_)
        high = torch.clamp(low + self.min_band_hz + torch.abs(self.band_hz_),self.min_low_hz,self.sample_rate/2)
        band=(high-low)[:,0]
        
        f_times_t_low = torch.matmul(low, self.n_)
        f_times_t_high = torch.matmul(high, self.n_)

        # Equivalent of Eq.4 of the reference paper (SPEAKER RECOGNITION FROM RAW WAVEFORM WITH SINCNET). 
        # I just have expanded the sinc and simplified the terms. This way I avoid several useless computations. 
        band_pass_left=((torch.sin(f_times_t_high)-torch.sin(f_times_t_low))/(self.n_/2))*self.window_ 
        band_pass_center = 2*band.view(-1,1)
        band_pass_right= torch.flip(band_pass_left,dims=[1])
        band_pass=torch.cat([band_pass_left,band_pass_center,band_pass_right],dim=1)
        band_pass = band_pass / (2*band[:,None])

        self.filters = (band_pass).view(
            self.out_channels, 1, self.kernel_size)

        return F.conv1d(waveforms, self.filters, stride=self.stride,
                        padding=self.padding, dilation=self.dilation,
                         bias=None, groups=1) 

SincNet 可解释性

带通滤波器源自数字信号处理，这使得 SincNet 第一层滤波器具有很好的可解释性，在频率上的可解释意义。

频域上的物理意义

• SincNet 第一层滤波器，即参数化、可学习的带通滤波器，复制了带通滤波器的特性与功能，因此，它的物理意义可以与带通滤波器相当——一维卷积的截至频 $f_1$ 与 $f_2$ 表示了特定任务所需的频域信息。

• 与二维卷积相同，SincNet 可以同时学习多个一维卷积，例如 SincNet 第一层滤波器是 80 个，这就使得该带通滤波器组具有物理统计意义——累积频率响应（下图红色实线 SincNet），即将 80 个滤波器组的通带累加，并归一化。此外，先前的 SincNet 讲解描述了 SincNet 相比较其与 CNN 学习的优势。

  

• 在累积频率响应的基础上，可以发现特定频率的信息对特定任务的重要性——占比小/归一化累积值低的频域范围的（针对任务的）重要性较低，例如下图 2 kHz - 2.5 kHz。

  

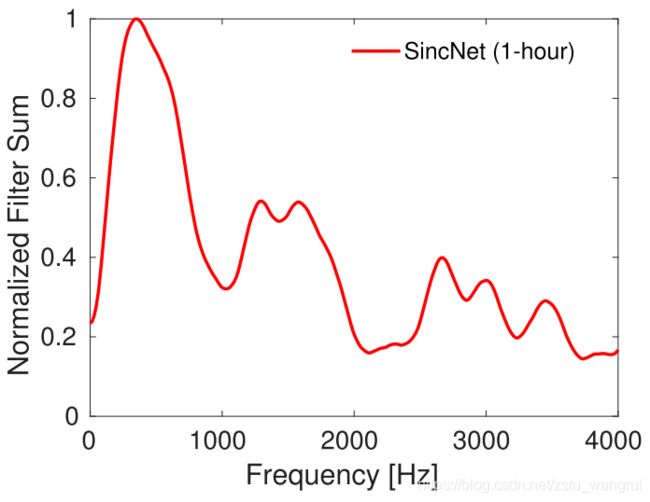
噪声场景的解释

噪声场景的语音处理任务是常见的问题，通常设计噪声鲁棒的表示学习和远距离/远场的语音处理，包含语音识别和说话人识别。

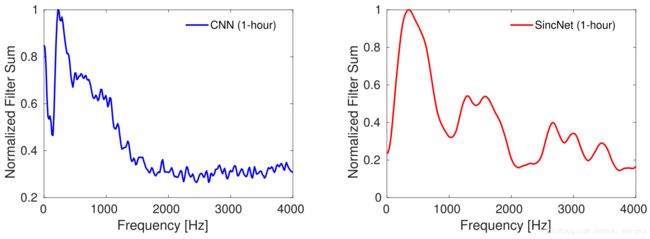
针对人为的特定频带的噪声，如上时频谱图，2 kHz - 2.5kHz 范围内有一个噪声。SincNet 可以更早（对比CNN）避免噪声带宽，如下图 1 小时训练后的累积频率响应。

基于 SincNet 无监督学习

根据 SincNet 作为说话人的紧凑表示形式，Ravanelli, M. 将其作为语音编码器，建立了一种无监督学习方法——Local Info Max (LIM)。在 TIMIT、Librispeech 与 VoxCeleb1 三个语料上，LIM 的性能超过了多种监督学习技术，该结论意味着一种潜在的可能：无监督学习方法获得的说话人嵌入，可以获得与监督学习更优或者相当的结果。

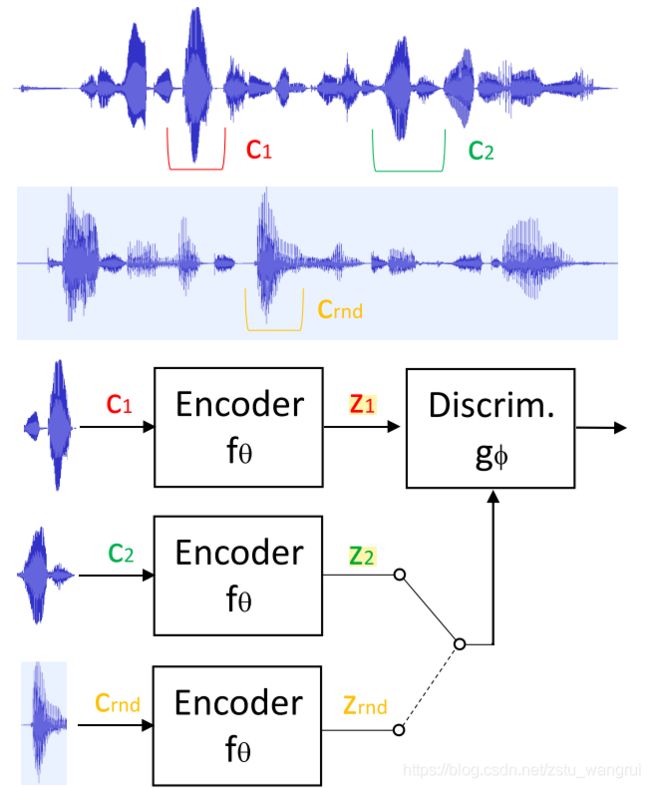
此外，在 LIM 的研究中，Ravanelli, M. 建立了两个巧妙假设：

1. 两个随机的语音段可能属于不同的说话人，
2. 每一段语音仅包含当个说话人。

第 2 个假设在常见的训练集中，通常都是成立的，因为大多数语音段都是按照不同说话人划分的；而第 1 个假设并不一定成立，特别是在每个说话人都包含大量语音段都时候，有可能来个随机的语音段可能属于相同的说话人，其概率大致为 $(n-1)/(m-1)$，其中 $n$ 为训练集中该说话人拥有的语音段数，$m$ 为总的语音段数。例如 $n=101,m=10001$，两个不同的语音段选择到同一说话人的概率为 $0.1$，即

$$(101-1)/(10001-1)=100/10000=0.01$$

由此可知，这一假设在“多目标说话人鉴别”或者大规模数据集中，其概率非常小，**这意味着假设 1 是显著可行的。**根据这两个假设，可以进一步形成一类无监督/自监督学习方法。

值得注意的是，本文采用了互信息 (Mutual Information, MI) 作为测量两个随机变量距离的方法，它不仅可以用作无监督学习的优化目标，仍可以作为监督学习模式的正则器。此外，MI 与判别器优化目标的一致性（都是最大化），使得该学习模型的优化过程相对容易，不会产生类似 GANs 的 min-max 博弈的优化问题。

这里列出 MI 数学模型 $MI(z_1,z_2)$ 和最简单有效的判别器损失 binary cross-entropy (BCE) $L(\Theta ,\Phi )$ 分别为：

$$MI(z_1,z_2)={\int }_{z_1}{\int }_{z_2}p(z_1,z_2)\log \left(\frac{p(z_1,z_2)}{p(z_1)p(z_2)}\right)d_{z_1}{d}_{z_2}=D_{KL}(p(z_1,z_2)\Vert p(z_1)p(z_2)),$$

$$L(\Theta ,\Phi )={\mathbb{E}}_{X_p}\left[\log (g(z_1,z_2))\right]+{\mathbb{E}}_{X_n}\left[1-\log (g(z_1,z_{rnd}))\right].$$

SincNet 对抗样本

研究说话人识别的对抗攻击具有两个主要应用：

1. 攻击应用：在非系统期望的情况下，扰动说话人识别系统；

2. 防御应用：帮助改善说话人识别系统的性能与鲁棒性。

考虑到 SincNet 是以原始波形作为输入，因而对抗攻击生成的扰动可以直接作用在原始波形上，产生攻击行为，这意味着 SincNet 的对抗攻击是可实现的，研究 SincNet 的对抗攻击具有必要性。

攻击者行为如下图所示，从模型的角度，攻击行为是建立一个攻击者模型，该模型在原始波形上加入对抗扰动，从而产生目标模型的误分类效果。其中攻击模型采用 adversarial transformation networks (ATNs)，该模型无需测试阶段的梯度信息。

另一方面，对抗攻击加入的扰动会对原有的声音造成影响，因此，单纯采用 $L_2$ 距离来衡量对抗扰动量并不合理，Li, J. 引入“心理声学” (psychoacoustic) 的感知质量和噪声扰动量来评价语音变化，具体地，PESQ (Perceptual Evaluation of Speech Quality) 与 SNR (Signal-to-Noise Ratio)。Non-targeted 攻击实现 99.2% 分类误差，扰动条件高达 57.2 dB SNR 与 4.2 PESQ。

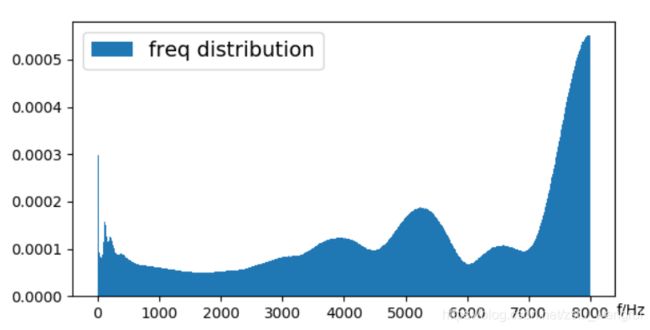
根据扰动的频谱分布可知，如上图，高频段（7 kHz - 8 kHz）较为显著，这一信息可以结合 SincNet 滤波器组的累积频率响应曲线进行分析，但论文中并未做进一步的研究。

这里有一个概念上的偏差，根据通俗的“累积频率响应(cumulative frequency response)或者累积频率图”的描述：累积频率用于确定位于数据集中特定值之上（或之下）的观察次数。
从这一点来看，SincNet 原文中的累积频率响应更像是一个频率统计分布：不同频率区间的滤波器数量统计，即横轴为频率，纵轴为频数的柱状分布图(hist)。

参考文献

本文中的所有图片来自参考文献。

1. Ravanelli, M., Bengio, Y., 2019. Speaker Recognition from Raw Waveform with SincNet, in: Proceedings of 2018 IEEE Spoken Language Technology Workshop (SLT). IEEE, Athens, Greece, pp. 1021–1028. https://doi.org/10.1109/SLT.2018.8639585
2. Ravanelli, M., Bengio, Y., 2018. Interpretable Convolutional Filters with SincNet, in: 32nd Conference on Neural Information Processing Systems (NIPS 2018) IRASL Workshop. Montréal, Canada.
3. Ravanelli, M., Bengio, Y., 2019. Learning speaker representations with mutual information, in: Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH. Graz, Austria, pp. 1153–1157. https://doi.org/10.21437/Interspeech.2019-2380
4. Li, J., Zhang, X., Xu, J., Zhang, L., Wang, Y., Ma, S., Gao, W., 2020. Learning to Fool the Speaker Recognition, in: ICASSP 2020 - 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). pp. 2937–2941. https://doi.org/10.1109/ICASSP40776.2020.9053058

---

作者信息：

CSDN：https://blog.csdn.net/i_love_home

Github：https://github.com/mechanicalsea

联系方式：2019 级同济大学博士研究生 王瑞 [email protected]

研究方向：说话人识别、说话人分离