《GPU高性能编程 CUDA实战》(CUDA By Example)读书笔记
写在最前
这本书是2011年出版的,按照计算机的发展速度来说已经算是上古书籍了,不过由于其简单易懂,仍旧被推荐为入门神书。先上封面:
![]()
由于书比较老,而且由于学习的目的不同,这里只介绍了基础代码相关的内容,跳过了那些图像处理的内容。
另外这本书的代码这里:csdn资源
前两章 科普
就各种讲CUDA的变迁,然后第二章讲如何安装CUDA。不会安装的请移步这里:安装CUDA.
第三章 CUDA C简介
输出hello world
#include__global__ void kernel() { printf("hello world"); } int main() { kernel<<<1, 1>>>(); return 0; } 这个程序和普通的C程序的区别值得注意
- 函数的定义带有了__global__这个标签,表示这个函数是在GPU上运行
- 函数的调用除了常规的参数之外,还增加了<<<>>>修饰。而其中的数字将传递个CUDA的运行时系统,至于能干啥,下一章会讲。
进阶版
#include__global__ void add(int a,int b,int *c){ *c = a + b; } int main(){ int c; int *dev_c; cudaMalloc((void**)&dev_c,sizeof(int)); add<<<1,1>>>(2,7,dev_c); cudaMemcpy(&c,dev_c,sizeof(int),cudaMemcpyDeviceToHost); printf("2 + 7 = %d",c); return 0; } 这里就涉及了GPU和主机之间的内存交换了,cudaMalloc是在GPU的内存里开辟一片空间,然后通过操作之后,这个内存里有了计算出来内容,再通过cudaMemcpy这个函数把内容从GPU复制出来。就是这么简单。
第四章 CUDA C并行编程
这一章开始体现CUDA并行编程的魅力。
以下是一个数组求和的代码
#include// copy the arrays 'a' and 'b' to the GPU
cudaMemcpy( dev_a, a, N * sizeof(int),
cudaMemcpyHostToDevice );
cudaMemcpy( dev_b, b, N * sizeof(int),
cudaMemcpyHostToDevice );
add<<1>>>( dev_a, dev_b, dev_c );
// copy the array 'c' back from the GPU to the CPU
cudaMemcpy( c, dev_c, N * sizeof(int),
cudaMemcpyDeviceToHost );
// display the results
for (int i=0; iprintf( "%d + %d = %d\n", a[i], b[i], c[i] );
}
// free the memory allocated on the GPU
cudaFree( dev_a );
cudaFree( dev_b );
cudaFree( dev_c );
return 0;
} 重点也是对于初学者最难理解的就是kernel函数了:
__global__ void add( int *a, int *b, int *c ) {
int tid = blockIdx.x;
if (tid < N)
c[tid] = a[tid] + b[tid];
}GPU编程和CPU编程的最大区别也就在这里体现出来了,就是数组求和竟然不要循环!为什么不要循环,就是因为这里的tid可以把整个循环的工作做了。这里的tid也就是thread的id,每个thread负责数组一个数的操作,所以将10个循环操作拆分成了十个线程同时搞定。这里的kernel函数也就是可以同时并发执行,而里面的tid的数值是不一样的。
第五章 线程协作
GPU逻辑结构
这章就开始介绍线程块和网格的相关知识了,也就是<<<>>>这里面数字的含义。首先讲一下什么叫线程块,顾名思义就是线程组成的块咯。GPU的逻辑结构如下图所示:
![]()
这个图来自NVIDIA官方文档,其中CTA就是线程块,Grid就是线程块组成的网格,每个线程块里有若干线程束warp,然后线程束内有最小的单位线程(文档里会称其为lanes,翻译成束内线程)。
基础知识稍微介绍一下,就开始介绍本章的内容了,本章的内容主要基于以下这个事实:
我们注意到硬件将线程块的数量限制为不超过65535.同样,对于启动核函数每个线程块中的线程数量,硬件也进行了限制。
由于这种限制的存在,我们就需要一些更复杂的组合来操作更大长度的数组,而不仅仅是使用threadIdx这种naive的东西了。
我们提供了以下的kernel来操作比较长的数组:
__global__ void add(int *a, int *b, int *c) {
int tid = threadIdx.x + blockIdx.x * blockDim.x;
while (tid < N) {
c[tid] = a[tid] + b[tid];
tid += blockDim.x * gridDim.x;
}
}嗯,理解透了int tid = threadIdx.x + blockIdx.x * blockDim.x;这句话,这章就算胜利完工了。首先,为啥是x,那有没有y,z呢,答案是肯定的,但是这里(对,就这本书里),用不上。其实线程块和网格都并不是只有一维,线程块其实有三个维度,而网格也有两个维度。因此存在.x的现象。当然我们不用管这些事,就当做它们只有一维好了。那就看下面这个图:
![]()
这就是只有一维的线程网格。其中,threadIdx.x就是每个线程在各自线程块中的编号,也就是图中的thread 0,thread 1。但是问题在于,每个block中都有thread 0,但是想让这不同的thread 0操作不同的位置应该怎么办。引入了blockIdx.x,这个就表示了线程块的标号,有了线程块的标号,再乘上每个线程块中含有线程的数量blockDim.x,就可以给每个线程赋予依次递增的标号了,程序猿们就可以操作比较长的数组下标了。
但是问题又来了,要是数组实在太大,我用上所有的线程都没办法一一对应咋办,这里就用tid += blockDim.x * gridDim.x;这句话来让一个线程操作很好几个下标。具体是怎么实现的呢,就是在处理过当前的tid位置后,让tid增加所以线程的数量,blockDim.x是一块中线程总数,而gridDim.x则是一个网格中所有块的数量,这样乘起来就是所有线程的数量了。
至此,线程协作也讲完了。再上一个更直观的图:
![]()
共享内存
共享内存是个好东西,它只能在block内部使用,访问速度巨快无比,好像是从离运算器最近的L1 cache中分割了一部分出来给的共享内存,因此巨快。所以我们要把这玩意用起来。
这里的例子是点积的例子,就是:
![]()
最后得到一个和。主要思想如下:
- 前一半加后一半:
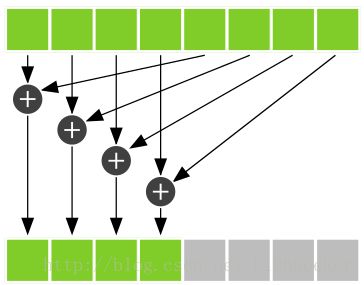
- 要同步,别浪
- 把最后的并行度小的工作交给CPU
具体代码是酱婶儿的:
__global__ void dot(float *a, float *b, float *c) {
//建立一个thread数量大小的共享内存数组
__shared__ float cache[threadsPerBlock];
int tid = threadIdx.x + blockIdx.x * blockDim.x;
int cacheIndex = threadIdx.x;
float temp = 0;
while (tid < N) {
temp += a[tid] * b[tid];
tid += blockDim.x * gridDim.x;
}
//把算出的数存到cache里
cache[cacheIndex] = temp;
//这里的同步,就是说所有的thread都要达到这里之后程序才会继续运行
__syncthreads();
//下面的代码必须保证线程数量的2的指数,否则总除2会炸的
int i = blockDim.x / 2;
while (i != 0) {
if (cacheIndex < i)
cache[cacheIndex] += cache[cacheIndex + i];
//这里这个同步保证了0号线程不要一次浪到底就退出执行了,一定要等到都算好才行
__syncthreads();
i /= 2;
}
if (cacheIndex == 0)
c[blockIdx.x] = cache[0];
}其中这个数组c其实只是所以结果中的一部分,最后会返回block数量个c,然后由cpu执行最后的加法就好了。
第九章 原子性操作
原子性操作,就是,像操作系统的PV操作一样,同时只能有一个线程进行。好处自然是不会产生同时读写造成的错误,坏处显而易见是增加了程序运行的时间。
计算直方图
原理:假设我们要统计数据范围是[0,255],因此我们定义一个unsigned int histo[256]数组,然后我们的数据是data[N],我们遍历data数组,然后histo[data[i]]++,就可以在最后计算出直方图了。这里我们引入了原子操作
__global__ void histo_kernel(unsigned char *buffer, long size,
unsigned int *histo) {
int i = threadIdx.x + blockIdx.x * blockDim.x;
int stride = blockDim.x * gridDim.x;
while (i < size) {
atomicAdd(&(histo[buffer[i]]), 1);
i += stride;
}
}这里的atomicAdd就是同时只能有一个线程操作,防止了其他线程的骚操作。但是,巨慢,书里说自从服用了这个,竟然比CPU慢四倍。因此我们需要别的。
升级版计算直方图
使用原子操作很慢的原因就在于,当数据量很大的时候,会同时有很多对于一个数据位的操作,这样操作就在排队,而这次,我们先规定线程块内部有256个线程(这个数字不一定),然后在线程内部定义一个临时的共享内存存储临时的直方图,然后最后再将这些临时的直方图加总。这样冲突的范围从全局的所有的线程,变成了线程块内的256个线程,而且由于也就256个数据位,这样造成的数据冲突会大大减小。具体见以下代码:
__global__ void histo_kernel(unsigned char *buffer, long size,
unsigned int *histo) {
__shared__ unsigned int temp[256];
temp[threadIdx.x] = 0;
//这里等待所有线程都初始化完成
__syncthreads();
int i = threadIdx.x + blockIdx.x * blockDim.x;
int offset = blockDim.x * gridDim.x;
while (i < size) {
atomicAdd(&temp[buffer[i]], 1);
i += offset;
}
__syncthreads();
//等待所有线程完成计算,讲临时的内容加总到总的直方图中
atomicAdd(&(histo[threadIdx.x]), temp[threadIdx.x]);
}第十章 流
- 页锁定内存
这种内存就是在你申请之后,锁定到了主机内存里,它的物理地址就固定不变了。这样访问起来会让效率增加。 - CUDA流
流的概念就如同java里多线程的概念一样,你可以把不同的工作放入不同的流当中,这样可以并发执行一些操作,比如在内存复制的时候执行kernel:
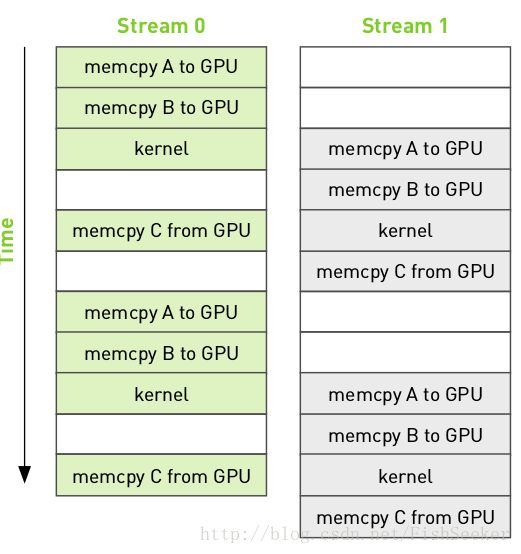
文后讲了一些优化的方法,但是亲测无效啊,可能是cuda对于流的支持方式变了,关于流的知识会在以后的博文里再提及。
十一章 多GPU
这章主要看了是第一节零拷贝内存,也十分好理解就是,在CPU上开辟一片内存,而GPU可以直接访问而不用复制到GPU的显存里。至于和页锁定内存性能上的差距和区别,需要实验来验证
===================2017.7.30更新========================
在阅读代码时发现有三种函数前缀:
(1)__host__ int foo(int a){}与C或者C++中的foo(int a){}相同,是由CPU调用,由CPU执行的函数
(2)__global__ int foo(int a){}表示一个内核函数,是一组由GPU执行的并行计算任务,以foo<<>>(a)的形式或者driver API的形式调用。目前global函数必须由CPU调用,并将并行计算任务发射到GPU的任务调用单元。随着GPU可编程能力的进一步提高,未来可能可以由GPU调用。
(3)__device__ int foo(int a){}则表示一个由GPU中一个线程调用的函数。由于Tesla架构的GPU允许线程调用函数,因此实际上是将__device__ 函数以__inline形式展开后直接编译到二进制代码中实现的,并不是真正的函数。
具体来说,device前缀定义的函数只能在GPU上执行,所以device修饰的函数里面不能调用一般常见的函数;global前缀,CUDA允许能够在CPU,GPU两个设备上运行,但是也不能运行CPU里常见的函数;host前缀修饰的事普通函数,默认缺省,可以调用普通函数。