Dijkstra算法Java实现

题目描述：

给定一个图，给定各个顶点之间的路径长度，求解从图中一个节顶点出发到任意节顶点的最短距离。

解题思路：

我们采用Dijkstra算法求解最短路径，Dijkstra算法采用广度优先搜索和贪心策略实现求解单源最短路径。选择离出发顶点最近的顶点并以这个顶点为中心调整出发顶点到那些周边顶点的最短距离，不断遍历并且修正，直到从出发顶点到任意顶点的权重修正完全。
例题图示：

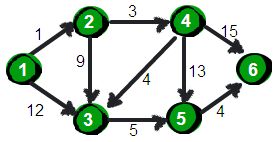
详细解题步骤：
1、把各个顶点之间的路径长度信息存入一个二维数组，再确定一个出发点，作为参数并调用获取最短路径的方法。

	public static void main(String[] args)
	{
		Test test = new Test();
		int MAX=Integer.MAX_VALUE-10000;
		int[][] weight={
				{0,1,12,MAX,MAX,MAX},
                {MAX,0,9,3,MAX,MAX},
                {MAX,MAX,0,MAX,5,MAX},
                {4,0,13,15,MAX,MAX},
                {MAX,MAX,MAX,MAX,0,4},
                {MAX,MAX,MAX,MAX,MAX,0}				
		};		
		int start=0;  //选择出发点
		int[] sp = test.getShortPath(weight,start);
		System.out.println(Arrays.toString(sp));
	}

2、定义一个数组保存各顶点是否被访问过，初始化为0,。因为我们从0号节点出发，设置0号顶点为已访问。

int[] visit = new int[weight.length]; //标记某节点是否被访问过
       for(int i:visit) //初始标记为未访问
    	   visit[i]=0;
       visit[start]=1; 

3、在循环中逐个访问每个顶点，并不断修正权重。

for(int k=1;k<=weight.length-1;k++) //循环中每次确定一个新的确定最短路径的节点

4、选择一个未标记的且离出发点最近的顶点。

 int dmin=Integer.MAX_VALUE;
    	   int position=0;
    	   //找出一个未标记的离出发点最近的节点
    	   for(int i=0;i<weight.length;i++)
    	   {
    		   if(visit[i]==0&&weight[start][i]<dmin&&i!=start)
    		   {
    			   dmin=weight[start][i];
    			   position=i;
    		   }
    	   }
    	   System.out.println("选出一个最短的路径："+dmin+"它是位置是："+position);
    	   //标记该节点为已经访问过
    	   visit[position]=1;

5、修正从出发顶点经由此顶点，再到其他顶点的最短路径。

 for(int i=1;i<weight.length;i++)
    	   {
    		  
    		   if(weight[start][position]+weight[position][i]<weight[start][i]&&i!=position)
    		   { 	
    			   System.out.println("原先的最短路径到"+i+"距离是:"+weight[start][i]);
    			   System.out.println("两者分别是"+weight[start][position]+","+weight[position][i]);
    			   weight[start][i]=weight[position][i]+weight[start][position]; //更新最短路径
    			   System.out.println("更新最短路径到"+i+"距离是:"+weight[start][i]);
    		   }
    	   }  	   

6、循环直到所有顶点被访问完。最后获取出发顶点到各个顶点的最短路径数组并返回。

int[] shortPath = new int[weight.length];
		for(int i=0;i<weight.length;i++)
			shortPath[i]=weight[0][i];
		return shortPath;

运行结果：
[0, 1, 10, 4, 15, 19]
顶点到自身的最短路径为0，到其余顶点的最短路径分别是1、10、4、15、19。