传统机器学习模型解说01：一元线性回归模型

引入

年薪和工作年限有关吗？

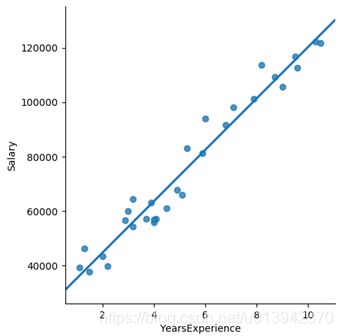
可见两个变量之间存在明显的线性关系，而根据常识，工作年限是因，年薪是果。
那么，是否存在某个模型，如图中的一次函数直线，来描述两个变量之间的关系呢？

原理简述与背景介绍

一元线性回归模型也被称为简单线性回归模型，指模型中只有一个自变量和一个因变量。
其原理可以简述为：用一个（二维中的）直线（以及高维中的超平面）去最大程度地拟合样本特征和样本输出标记（即数据点）之间的关系。
一元线性回归思想简单，但背后有强大的数学理论支持，具有很好的可解释性，是许多强大的非线性模型的基础。

算法推导

基本设定

给定数据集$$T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_N,y_N\right)\right\}$$其中$x_i\in \mathcal{X}\subseteq \mathbb{R}$，$y_i\in \mathcal{Y}\subseteq \mathbb{R}$，$i=1,2,\cdots ,N$
假设决策函数为$$f(x)=ax+b$$其中$a,b$称为回归系数。
可知第$i$个元素$x_i$的预测值为$$\widehat{y_i}=f(x_i)=a{x}_i+b$$使用平方损失函数作为损失函数：$$L\left(y,f(x)\right)={\left(y-f(x)\right)}^2$$求以下经验风险最小化$$J(a,b)=\sum _{i=1}^N(y_i-\widehat{y_i}{)}^2=\sum _{i=1}^N{\left(y_i-a{x}_i-b\right)}^2$$即目标是求取使目标函数$J$最小的回归系数$a,b$.

参数求解

1. 求解$b$

对$b$求偏导并另令其等于$0$
$$\frac{\partial J(a,b)}{\partial b}=\sum _{i=1}^{N}2\left(y_i-a{x}_i-b\right)(-1)=0$$去除系数，即得$$\sum _{i=1}^N\left(y_i-a{x}_i-b\right)=0$$展开得到$$\sum _{i=1}^N{y}_i-a\sum _{i=1}^N{x}_i-\sum _{i=1}^{N}b=0$$由于$b$是常数，最后一项可以改写为$$\sum _{i=1}^N{y}_i-a\sum _{i=1}^N{x}_i-Nb=0$$因此移项得到$$Nb=\sum _{i=1}^N{y}_i-a\sum _{i=1}^N{x}_i$$注意到左边有所有$y$值的和与所有$x$的值，因此如果左右两边都除以$N$值，将得到$$b=\overline{y}-a\overline{x}$$其中$\overline{y},\overline{x}$分别是所有$y,x$的均值。

2. 求解$a$

对$a$求偏导并令其等于$0$
$$\frac{\partial J(a,b)}{\partial a}=\sum _{i=1}^{N}2\left(y_i-a{x}_i-b\right)\left(-x_i\right)=0$$去除系数得到$$\sum _{i=1}^N\left(y_i-a{x}_i-b\right)x_i=0$$将$b=\overline{y}-a\overline{x}$代入得到$$\sum _{i=1}^N\left(y_i-a{x}_i-\overline{y}+a\overline{x}\right)x_i=0$$将$x_i$乘入得到$$\sum _{i=1}^N\left[y_i{x}_i-a(x_i{)}^2-\overline{y}{x}_i+a\overline{x}{x}_i\right]=0$$可以看到系数$a$在第二项和第四项，拆开并提取$a$得到$$\sum _{i=1}^N(y_i{x}_i-\overline{y}{x}_i)-a\sum _{i=1}^N[(x_i{)}^2-\overline{x}{x}_i]=0$$移项并作除法得到$$a=\frac{{\sum }_{i=1}^N\left(x_i{y}_i-x_i\overline{y}\right)}{{\sum }_{i=1}^N\left[(x_i{)}^2-x_i\overline{x}\right]}$$计算结束。

3. 优化

考虑到$\overline{y},\overline{x}$都是定值，有以下等式：
$$\sum _{i=1}^N{x}_i\overline{y}=\overline{y}\sum _{i=1}^N{x}_i=N\overline{y}\overline{x}=\overline{x}\sum _{i=1}^N{y}_i=\sum _{i=1}^N\overline{x}{y}_i=\sum _{i=1}^N\overline{x}\ast \overline{y}$$
同理有$$\sum _{i=1}^N{x}_i\overline{x}=\overline{x}\sum _{i=1}^N{x}_i=\overline{x}N\overline{x}=N(\overline{x}{)}^2=\sum _{i=1}^N(\overline{x}{)}^2$$因此对于$a$有$$a=\frac{{\sum }_{i=1}^N\left(x_i{y}_i-x_i\overline{y}\right)}{{\sum }_{i=1}^N\left[(x_i{)}^2-x_i\overline{x}\right]}=\frac{{\sum }_{i=1}^N\left(x_i{y}_i-x_i\overline{y}-\overline{x}{y}_i+\overline{x}\ast \overline{y}\right)}{{\sum }_{i=1}^N\left[{\left(x_i\right)}^2-\overline{x}{x}_i-\overline{x}{x}_i+(\overline{x}{)}^2\right]}=\frac{{\sum }_{i=1}^N\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{{\sum }_{i=1}^N{\left(x_i-\overline{x}\right)}^2}$$
可见这样可以极大地提升计算效率。

4. 答案

以下为答案：
$$\{\begin{array}{l}a=\frac{{\sum }_{i=1}^N\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{{\sum }_{i=1}^N{\left(x_i-\overline{x}\right)}^2}\\ b=\overline{y}-a\overline{x}\end{array}$$

代码实现

数据介绍

使用seaborn自带的tips数据集

import pandas as pd
import seaborn as sns
tips=sns.load_dataset('tips')
tips.head()

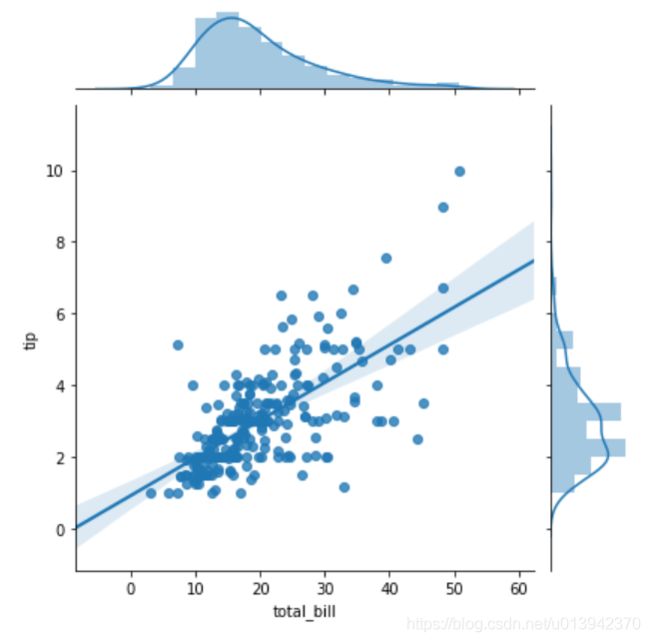
我们选取前两列，total_bill总消费作为自变量x，tip小费作为因变量y，画出两者的关系图如下：

sns.jointplot(x='total_bill',y='tip',data=tips,kind='reg')

可见两者存在线性关系，且可以用一条直线大致拟合。

自制代码实现

def simpleRegression(x,y):
    xMean=x.mean()
    yMean=y.mean()
    a=((x-xMean)*(y-yMean)).sum()/(x-xMean).pow(2).sum()
    b=yMean-xMean*a
    return a,b

simpleRegression(tips['total_bill'],tips['tip'])

前者是$a$的值，后者是$b$的值。

sklearn代码实现

from sklearn import linear_model
lr=linear_model.LinearRegression()
x=tips[['total_bill']]#注意这里必须要加两个方括号，xy都是
y=tips[['tip']]
res=lr.fit(x,y)

res.coef_[0][0],res.intercept_[0]

可见两组答案数字在小数点后10位都是一样的，可以说是基本一致。

参考资料

1. https://blog.csdn.net/thfyshz/article/details/83589836
2. https://zhuanlan.zhihu.com/p/76580358
3. 《从零开始学Python数据分析与挖掘》，第7章