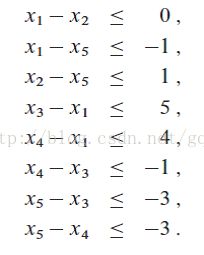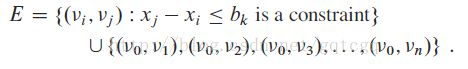最短路径问题:一个带权重的有向图G = (V, E)和权重函数w: E->R,该权重函数将每条边映射到实数值的权重上。一条路径p的权重w(p)是构成该路径的所有边的权重之和,定义从节点u到结点v的最短路径权重δ (u, v)如下:
在实际应用中,可以用一张图表示道路交通图,结点代表城市,边代表城市之间的道路,边上的权重代表道路的长度。目标就是找出一条从城市A到城市B的最短路径,边上的权重还可以表示时间、费用、罚款、损失或者任何随路径长度的增加而线性积累的,并且需要最小化的数量。
广度优先搜索算法就是一个求取最短路径的算法,但该算法只能用于无权重的图,即每条边的权重都是单位权重的图。
本章讨论单源最短路径问题:给定图G=(V, E),希望找到从给定源节点s到每个结点v的最短路径。单源最短路径可以有下面的变体:
单目的地最短路径问题:找出从每个顶点v到指定终点t的最短路径。把图中的每条边反向,就可以把这一问题变为单源最短路径问题。
单结点对最短路径问题:找到从给定结点u到给定结点v的最短路径。解决了单源最短路径问题,则这一问题也就获得解决。
所有节点对最短路径问题:对于每对顶点u和v,找出从u到v的最短路径。虽然将每个顶点作为源点,运行一次单源算法就可以解决这一问题,但通常可以更快地解决这一问题,下一章将详细讨论这个问题。
一:概述
1:最短路径的最优子结构
最短路径具有最优子结构性质:两个结点之间的一条最短路径包含其他的最短路径:
给定带权重的有向图G=(V, E)和权重函数w。设p=<![]() >为从节点
>为从节点![]() 到结点
到结点![]() 的一条最短路径,并且对于任意的i, j, 0 <= i <= j <= k,设
的一条最短路径,并且对于任意的i, j, 0 <= i <= j <= k,设![]() = <
= <![]() >为路径p中从节点
>为路径p中从节点![]() 到结点
到结点![]() 的子路径。那么
的子路径。那么![]() 是从
是从 到节点
到节点![]() 的一条最短路径。
的一条最短路径。
2:负权重的边
边的权重可以为负值,即使边的权重为负值,对于所有节点v,最短路径权重 (u, v)都可以有精确定义。但是,如果图G=(V, E)包含从源节点s可以到达的,权重为负值的环路,则最短路径权重无定义,从s到该环路上的任意节点的路径都不可能是最短路径。如果从节点s到节点v的某条路径上存在权重为负值的环路,则(u, v) = -∞。
如下图所示:
从节点s到节点c有无数条路径;
从节点s到节点e也有无数条路径:
节点
4:环路
最短路径不能包含权重为负值的环路。而且,最短路径也不能包含权重为正值得环路。因为只要将环路从路径上删除就可以得到一条权重更小的路径。
如果从s到节点v存在一条包含权重为0的环路的最短路径,则将该环路删除之后,就可以得到另外一条最短路径。
所以,假定找到的最短路径上没有环路,即它们都是简单路径。由于图G=(V, E)的任意无环路径最多包含|V|个不同的节点,因而最多包含|V|-1条边。
5:最短路径的表示
除了需要计算最短路径的权重,还需要计算最短路径上的节点。给定图G=(V, E),对于每个节点v,需要维持前驱节点v.π 。本章的最短路径算法将对每个节点的π属性进行设置,给定节点v,如果v.π != NULL,则PRINT-PATH(G, s, v)就能打印出从节点s到v的一条最短路径。
定义图G 的前驱子图![]() = (
= ( ![]() ),其中
),其中![]() 是图G中的前驱节点不是NULL的节点的集合。同时,还包含源节点s,所以:
是图G中的前驱节点不是NULL的节点的集合。同时,还包含源节点s,所以:![]() = {v ∈ V;v.π != NULL} ∪ {s}。而
= {v ∈ V;v.π != NULL} ∪ {s}。而 ![]() = {(v.π, v) ∈ E;v ∈ v-{s} }。
= {(v.π, v) ∈ E;v ∈ v-{s} }。
当算法终止时,![]() 是一颗“最短路径树”,非形式化的说,最短路径树是一颗根节点为s的树,该树包括了从源节点s到每个可以从s到达的节点的一条最短路径。更精确的定义如下:
是一颗“最短路径树”,非形式化的说,最短路径树是一颗根节点为s的树,该树包括了从源节点s到每个可以从s到达的节点的一条最短路径。更精确的定义如下:
设图G=(V, E)是一条带权重的有向图,权重函数为w,并假定G中不包含从源点s可以到达的权重为负值的环路,因此所有的最短路径都有定义。一颗根节点为s的最短路径树是一个有向子图G’ = (V’ , E’),V’![]() , E’
, E’![]() E,满足:
E,满足:
a:V’是图G中从源节点s可以到达的所有节点的集合
b:G’形成一颗根节点为s的树
c:对于所有的节点v ∈ V’,图G’中从节点s到v的唯一简单路径是G中从节点s到v的一条最短路径。
另外,最短路径不是唯一的,最短路径树也不一定是唯一的。
6:松弛操作
每个节点v,维持一个属性v.d,表示从源节点s到节点v的最短路径权重的上届。通过下面的运行时间为O(V)的算法来对v.d和v.π 进行初始化:
INITIALIZE-SINGLE-SOURCE(G, s)
for each vertex v ∈ G.V
v.d = ∞
v.π = NIL
s.d = 0
下面的算法就是对边(u, v)在O(1)时间内进行的松弛操作:
RELAX(u, v, w)
if v.d > u.d + w(u, v)
v.d = u.d + w(u, v)
v.π = u
如下图就是对一条边进行松弛的例子,第一个例子,v.d因松弛操作而减少了,第二个例子却没有变化:
本章中的每个算法都会调用INITIALIZE-SINGLE-SOURCE,然后重复对边进行松弛的过程。另外,松弛是改变最短路径估计v.d和前趋v.π的唯一方式。本章中的算法之间的区别在于对每条边进行松弛操作的次数,以及对边执行松弛操作的次序有所不同。
7:最短路径和松弛操作的性质
a:三角不等式性质:对于任何边(u,v) ∈ E,有 δ(s, v)<= δ(s, u) +w(u, v)。
b:上届性质:对于所有的节点v∈ V,我们总有v.d >= δ(s, v)。一旦v.d的取值达到 δ(s, v),其值将不再发生变化。
c:非路径性质:如果从节点s到节点v之间不存在路径,则总有v.d = δ(s, v) = ∞。
d:收敛性质:对于某些节点u, v ∈V,如果s ~> u-> v是图G中的一条最短路径,并且对边(u, v)进行松弛前的任意时间有u.d = δ(s, u),则在对边(u, v)松弛之后的所有时间v.d =δ(s, v)。
e:路径松弛性质:如果p=<![]() >是从源节点s =
>是从源节点s =![]() 到
到![]() 的一条最短路径,并且对p中的边进行松弛的次序为(
的一条最短路径,并且对p中的边进行松弛的次序为(![]() ), (
), (![]() ), ..., (
), ..., (![]() ),则
),则![]() .d =δ(s, v)。该性质的成立与任何其他的松弛操作无关,即使这些松弛操作是与对p上的边所进行的松弛操作穿插进行的。
.d =δ(s, v)。该性质的成立与任何其他的松弛操作无关,即使这些松弛操作是与对p上的边所进行的松弛操作穿插进行的。
f:前驱子图性质:对于所有的节点v∈ V,一旦v.d =δ(s, v),则前驱子图是一颗根节点为s的最短路径树。
注意:假定对于任意实数a != -∞,有a +∞ =∞ + a =∞ ,如果a !=∞ ,有a +(-∞) = (-∞)+ a =-∞ 。
本章所有的算法都假设有向图G用邻接表的形式存储。
二:Bellman-Ford算法
Bellman-Ford算法解决的是一般情况下的单源最短路径问题,边的权重可以为负值,同时,该算法返回一个布尔值,来表明是否存在一个从源节点可以到达的权重为负值的环路。如果存在负值环路,则算法没有解决方案,如果不存在,算法给出最短路径以及权重。
BELLMAN-FORD(G,w, s)
INITIALIZE-SINGLE-SOURCE(G, s)
for i = 1 to |G.V|-1
for each edge (u, v)∈ E
RELAX(u, v, w)
for each edge (u, v) ∈ E
if v.d > u.d + w(u, v)
return FALSE
return TRUE
该算法返回TRUE表明图中不包含从源节点可达的负值环路。算法对图中的每条边进行|G.V|-1的处理,下图为实例:
该算法第一行的初始化需要O(V)的时间,第2-4行的循环时间为O(E),且一共需要|G.V|-1 次循环,第5-7行的时间为O(E),所以,Bellman-Ford算法的总运行时间为O(VE)。
该算法的正确性证明:在该算法的2-4行的for循环中,每次循环对每条边都进行松弛。在第i次循环中,被松弛的边肯定包括(![]() ),所以根据松弛定理得证正确。对于是否具有环路而返回TURE或FALSE,参见P380。
),所以根据松弛定理得证正确。对于是否具有环路而返回TURE或FALSE,参见P380。
三:有向无环图中的单源最短路径问题
该算法针对有向无环图,根据结点的拓扑排序的次序来进行边的松弛操作,可以在O(V+E)时间内计算出源节点到所有节点的最短路径。有向无环图中的边权重可以为负值。
DAG-SHORTEST-PATHS(G,w, s)
topologically sort the vertices of G
INITIALIZE-SINGLE-SOURCE(G,s)
for each vertex u, taken in topologically sorted order
for each vertex v∈ G.Adj[u]
RELAX(u,v, w)
下图描述了概算法的一个实例:
该算法第一行的拓扑排序时间为O(V+E),初始化时间为O(V),外循环针对每个结点,因此内循环针对每条边,所以算法的总运行时间为O(V+E)。该算法之所以正确,就是因为拓扑排序![]() ,表明了存在边(
,表明了存在边(![]() ),所以根据松弛定理可证。
),所以根据松弛定理可证。
四:Dijkstra算法
该算法要求所有边的权重为非负值,如果采用合适的实现方式,Dijkstra算法的运行时间要比Bellman-Ford算法快。
该算法维护集合S,从源节点s到S中每个节点的最短路径已经被找到,该算法要用到最小优先队列:
DIJKSTRA(G, w, s)
INITIALIZE-SINGLE-SOURCE(G, s)
S = ∅
Q =G.V
while Q != ∅
u = EXTRACT-MIN(Q)
S= S ∪ {u}
for each vertex v ∈ G.Adj[u]
RELAX(u, v, w)
该算法维持的不变式是Q=V-S,该算法总是选择Q中最近的节点加入到S中,使用的是贪心策略。下图为算法执行示例:
虽然贪心策略不一定能够得到最优解,但是使用贪心策略的Dijkstra算法确实能够得到最优解,这是因为每次选择节点u加入到集合S时,都有u.d = δ(s,u)。
该算法执行三种优先队列:INSERT, EXTRACT-MIN, DECREASE-KEY(隐含在RELAX中)。对每个节点调用一次INSERT和EXTRACT-MIN,最多对每条边进行一次DECREASE-KEY操作。
如果对图中的节点进行从1到|V|的编号,然后用|V|大小的数组来维持优先队列,将v.d存放在数组的第v个索引中,则每次INSERT和DECREASE-KEY执行时间为O(1),每次EXTRACT-MIN的操作时间为O(V)。所以,算法运行总时间为O(![]() )= O(
)= O(![]() )
)
如果讨论的是稀疏图,则可以使用二叉堆,算法总运行时间为O((V+E)lg V)。如果使用斐波那契堆实现最小队列,则时间可以减少到O(Vlg V + E)。
五:差分约束和最短路径
给定一个m*n的矩阵A,一个m维的向量b,希望找到一个n维向量x,满足Ax<= b。也需要能够分析不出存在这样的解的情况。
这种问题的特例是差分约束系统,其中矩阵A的每一行包括一个1和一个-1,其他所有项为0。因此,Ax <= b所给出的约束条件变为m个涉及n个变量的差额限制条件,每个约束条件的形式为:![]() <=
<=![]() 。比如,下面的问题:
。比如,下面的问题:
这个问题与寻找满足下列8个差分约束条件的变量![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的问题等价:
的问题等价:
这样的问题答案有多个:如果向量x=(![]() ,
, ![]() )是差分约束系统Ax<=b的一个解,设d为任意常数,则x+d = (
)是差分约束系统Ax<=b的一个解,设d为任意常数,则x+d = (![]() +d,
+d,![]() )也是该差分约束系统的一个解。
)也是该差分约束系统的一个解。
差分约束系统可以用许多不同的应用:例如, ![]() 可以是事件将要发生的时刻,每个约束条件可以解释为两件事情之间必须间隔的最短时间或者最长时间。
可以是事件将要发生的时刻,每个约束条件可以解释为两件事情之间必须间隔的最短时间或者最长时间。
可以从图论的角度来解决差分约束系统,可以把m*n的矩阵A看做n个节点,m条边的有向图,图中每个节点![]() 对应于某个
对应于某个 ![]() ,每条边则对应一个不等式。正式的说:
,每条边则对应一个不等式。正式的说:
给定差分约束系统Ax <= b,其对应的约束图是一个带权重的有向图G=(V, E),这里:
约束图中包含一个额外的节点 ![]() ,从其出发可以到达所有其他的节点。如果
,从其出发可以到达所有其他的节点。如果![]() <=
<= ![]() 是一个差分约束条件,则边(
是一个差分约束条件,则边(![]() ,
, ![]() )的权重为
)的权重为![]() 。所有从节点
。所有从节点![]() 发出的边权重为0,如下图:
发出的边权重为0,如下图:
可以通过在约束图中寻找最短路径来得到差分约束系统的一个解,如果G不包含权重为负值的环路,则![]() 是一个可行解,如果G中包含负值环路,则该系统没有可行解。
是一个可行解,如果G中包含负值环路,则该系统没有可行解。
可以用Bellman-Ford算法解决差分约束系统,如果该算法返回TRUE,则最短路径权重给出的是一个可行解,否则,表明没有可行解。因为约束图有n+1个节点和m+n条边,所以算法运行时间为O(![]() ),可以对该算法进行优化使得时间为O(nm)。
),可以对该算法进行优化使得时间为O(nm)。