记一下机器学习笔记 最小均方（LMS）算法

这里是《神经网络与机器学习》第三章的笔记…
最小均方算法，即Least-Mean-Square，LMS。其提出受到感知机的启发，用的跟感知机一样的线性组合器。
在意义上一方面LMS曾被用在了滤波器上，另一方面对于LMS的各种最优化方式为反向传播算法提供了思想基础。

于是这章书主要是简单介绍LMS算法的原理，并介绍几个简单的最优化方法，然后用物理热力学原理描述LMS算法的学习过程（这个部分太过高深只好跳过）

LMS滤波结构

原理上跟感知机也差不多，也是对包含一组共 M 个元素的 x1,x2,...,xM 的输入用一个线性组合器处理，也就是对其进行加权求和，得出结果 y ，与期望响应 d 相比较，获得误差信号 e ，并由此修正权值，如下图：

这里比感知机还要简单的，直接将局部诱导域 v 作为输出 y 。因此可以表述成：

y(i)=w1(i)x1(i)+w2(i)x2(i)+...+wM(i)xM(i)=∑k=1Mwk(i)xk(i)

或者写成向量的形式：

y(i)=x(i)Tw(i)

w(i) 即权值向量 [w1(i),w2(i),...,wM(i)]T ， i 表示迭代次数。
误差信号为期望响应跟输出的差，即：

e(i)=d(i)−y(i)

无约束最优化问题

LMS算法的目标就是找到一组权值向量，使其输出响应跟期望响应最接近。

设立一个代价函数 E(w) ，其对权值向量连续可微，用来描述输出响应跟期望响应的差距，也就是值越小越好。于是我们的目标就是酱紫：
找到一个最优的权值向量 w∗ ，对于任何 w 都有：

E(w∗)≤E(w)

这是一个无约束最优化问题。其解决的一个必要条件就是 ∇E(w)=0 。
也就是：

[∂E∂w1,∂E∂w2,...,∂E∂wM]T=0

一般的解决方法是从一个初始权值向量 w(0) 开始，不断迭代产生新的权值向量 w(i) ，对于每一个权值向量其代价函数都要小于上一个的代价函数，即 E(w(i))<E(w(i−1)) ，如此往复直到代价函数足够小为止。或者说在一个M维的空间里，从一个点出发，不停地往代价函数减小的方向走，直到走到最低点。

最速下降法

也就是反向传播算法梯度下降的基本原理，在每一个位置 w(i) 求出当前位置的代价函数的梯度 g(i) ，再沿着梯度的反方向（正方向使代价函数增加）移动一段距离成为 w(i+1) ，也就是每次都顺着坡最陡的方向往下走一步。
梯度即为代价函数对权值向量的每一个元素求偏导：

g=∇E(w)=∂E∂w

权值向量的修正为：

w(i+1)=w(i)−ηg(i)

η 为一个标量，称为步长或学习率参数，可以理解为沿着梯度方向走的一步的大小。

理论上来说学习率参数 η 在足够小的时候，才能完全保证权值向量的修正是让代价函数一步比一步小的。但是 η 太小又会导致收敛速度过慢。

定义代价函数：

E(w)=12∑i=1N(di−yi)2=12∑i=1N(di−wTxi)2

那么就有：

g=∂(12∑i=1N(di−wTxi)2)/∂w=−∑i=1Neixi

其中 ei=di−wTxi 即误差值。于是权值向量的修正为：

w(i+1)=w(i)−ηg(i)=w(i)+η∑i=1Neixi

N为样本数量。

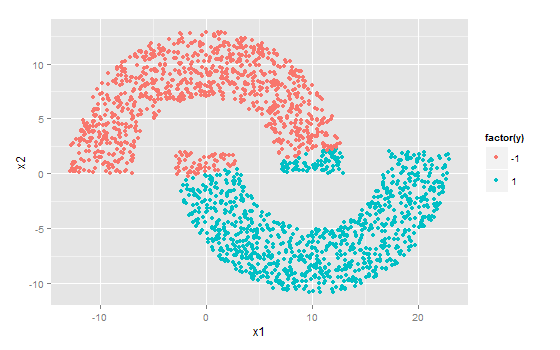
在R代码实现里依然使用感知机的双月牙二分数据集…这回月牙间距设为-2：

在R代码中该点集为X，共有2000个点被分到两个月牙上：

> X
              x1         x2
 [1,]   5.394098 11.3201659
 [2,]  -6.590109  4.3553063
 [3,]   7.481122  4.3304918
 [4,]  -5.727646  8.1037834
 [5,]  -5.526536  6.9770548
 [6,]   1.440511  1.5264444
 [7,]  14.089176 -7.2411777
 [8,]   3.846768 -1.9579111
 [9,]   6.874768 -4.6271839
[10,] -10.922336  2.9085794
...

R中%*%为矩阵相乘符号，t()为矩阵转置。

# X为点的坐标数据集，d为各点的正确分类，即期望响应，值为-1和1。

W = c(0,0) #初始化权值向量
eta = 1e-6 #学习率参数
n = 50       #迭代次数

MSE = c()    #初始化均方差数组

for(i in 1:n){
  y = X %*% W
  e = d - y          #计算分类误差
  MSE[i] = mean(e**2) #记录每一步的均方差

  W = W + eta * t(X) %*% e # 修正权值
}

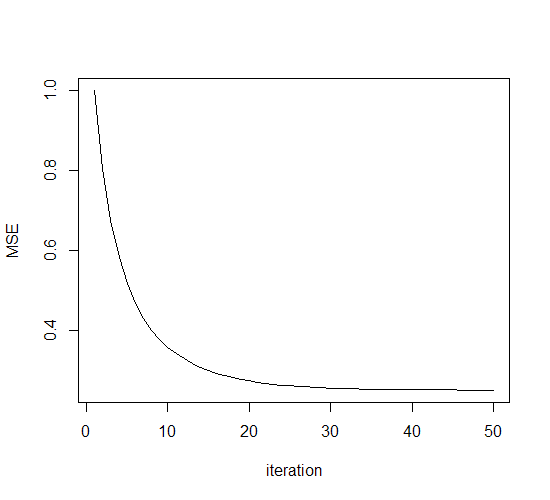
plot(MSE,type='l',xlab='iteration') #绘制均方差变化曲线

y = sign(X %*% W)
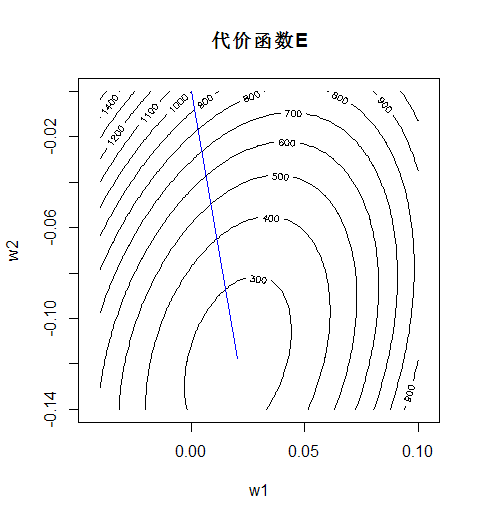
qplot(x1,x2,color=factor(y)) #绘制分类结果

分类结果是酱紫的。毕竟本来就是线性不可分的点集。

这里的学习率参数设为了一个较小的值1e-6。可见此时权值向量修正的轨迹是很平滑的：

然而收敛的速度就不太尽人意了。

接下来将学习率参数 η 改为一个较大的值7.5e-6：

可见权值向量的轨迹从平滑变成了抖动。

而相对的，收敛速度快了…

牛顿法

最速下降法也可以理解为是拿一个平面去拟合点附近的曲面，而牛顿法则是复杂一些，拿一个二阶的曲面去拟合点附近的曲面。
具体来说就是拿代价函数在权值向量 w(i) 处二阶泰勒展开（最速下降法可认为是一阶泰勒展开）：

ΔE(w)=E(w(i)+Δw)−E(w(i))=gT(i)Δw+12ΔwTH(i)Δw

其中 H 为Hessian矩阵：

H=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂2E∂w21∂2E∂w2∂w1⋮∂2E∂wM∂w1∂2E∂w1∂w2∂2E∂w22⋮∂2E∂wM∂w2⋯⋯⋱⋯∂2E∂w1∂wM∂2E∂w2∂wM⋮∂2E∂w2M⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

说白了就是对不同组合的权值求两次偏导。

接着就是要最大化 ΔE(w) ，所以拿上上式右边对权值向量求导后再使之为0：

g(i)+H(i)Δw=0

解得 Δw=−H−1(i)g(i) 。
也就是 w(i+1)=w(i)−H−1(i)g(i) 。

牛顿法的主要问题就是计算复杂度，以及其要求Hessian矩阵 H 每次迭代里都必须是正定的但这不好保证。

对于代价函数是这样的情况：

E(w)=12∑i=1N(di−yi)2=12∑i=1N(di−wTxi)2

拿代价函数对权值求两次偏导，可以算得Hessian矩阵 H 的第i行第j列的元素为：

hij=−∑s=1Nxi(s)xj(s)

其中N为样本数量，s表示第s个样本。
因而Hessian就为：

H=XTX

其中 X 为样本矩阵，一行一样本一列一属性。

那么训练的R脚本就是酱紫：

H = t(X) %*% X #计算Hessian矩阵

W = c(0,0) #初始化权值向量
n=50

for(i in 1:n){
  y = X %*% W
  e = d - y

  g = - t(X) %*% e 
  W = W - solve(H) %*% g #按照公式修正权值
}

R中函数solve()可以求解矩阵的逆。
结果发现一次迭代就直接走到了最优值。

高斯-牛顿法

为了降低牛顿法的计算量同时保证收敛能力又提出了高斯-牛顿法。其优势就是不需要搞两次偏导。
依然是用这个误差平方和一半的代价函数：

E(w)=12∑i=1N(di−yi)2=12∑i=1Ne2i

不过这次就不先拿代价函数，而是拿误差信号 ei 对权值向量在某一点处作一阶泰勒展开：

e′i(w)=ei(w(n))+[∂ei∂w]T(w−w(n))

这回i表示第i个样本，而n表示第n次迭代。
把所有样本的 e′i 组合成列阵形式，就有：

e′(w)=e(w(n))+J(n)(w−w(n))

其中 e′=[e′1,e′2,...,e′N]T ，N为样本数量。
J 为Jacobi矩阵：

J=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂e1∂w1∂e2∂w1⋮∂eN∂w1∂e1∂w2∂e2∂w2⋮∂eN∂w2⋯⋯⋱⋯∂e1∂wM∂e2∂wM⋮∂eN∂wM⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

说白了就是每个样本的误差信号分别对每个权值求偏导。

那么误差信号就是：

E(w)=12∥e′(w)∥2=12∥e(w(n))∥2+e(w(n))TJ(n)(w−w(n))+12(w−w(n))TJ(n)TJ(n)(w−w(n))

矩阵形式的完全平方公式。两根竖线 ∥ 表示欧几里得范数，也就是常说的向量的模。
现在需要找到一个权值向量使上式最小作为 w(n+1) ，于是对上式对权值向量求导并使之为0，得：

JT(n)e(n)+JT(n)J(n)(w−w(n))=0

解出 w 作为 w(n+1) 得：

w(n+1)=w(n)−(JT(n)J(n))−1JTe(n)

这就是高斯-牛顿法的基本型。

自然这里还有要求 JT(n)J(n) 得是非负定的。于是通常会给它加上一个对角矩阵 δI 。 δ 是一个较小的正数， I 是单位矩阵。于是上式就变成：

w(n+1)=w(n)−(JT(n)J(n)+δI)−1JTe(n)

维纳滤波器

然后接着推导。在这里误差信号为 ei=di−yi=di−wTxi
于是有 ∂ei∂w=−xi ， e′i(w)=ei(w(n))−xi 。
从而Jacobi矩阵为：

J=[−x1,−x2,...,−xN]T=−X

X 就是样本矩阵。
另外可知有 e=d−Xw 。
将这些带入到高斯-牛顿法的基本型中可得：

w(n+1)=w(n)+(XT(n)X(n))−1XT(d(n)−Xw(n))

整理之后你会发现 w(n) 会被消掉，然后就干脆成了：

w(n+1)=(XT(n)X(n))−1XT(n)d(n)

简直可以一开始就一次计算啊。也难怪前边用牛顿法可以一次就收敛。
然后定义 X 的伪逆为 X+=(XT(n)X(n))−1XT 。这样就可以表述成最优权值向量为样本矩阵的伪逆乘上期望响应：

w(n+1)=X+d(n)

这就像是《神机》第二章所讲的一次性计算分界的线性最小二乘分类器，所以这也叫 线性最小二乘滤波器。
当样本数量N趋于无穷时，就成了维纳滤波器。

R语言中用行代码即可算得权值向量：

W = solve(t(X) %*% X) %*% t(X) %*% d

最小均方算法

反正《神机》是过了前面的大堆篇幅之后才开始讲回这章的主题…
其实所谓最小均方算法就是拿均方误差作为代价函数，并使之最小的算法，权值调整方法也是跟最速下降法一致。
只不过不同的是，前面的几个方法都是计算汇总了所有样本的误差再调整，而这里是逐个样本逐个计算误差逐个调整。每一个样本称为一个瞬像。
因为每个样本不同，每次权值调整的方向也不同而近似于随机，但是总体来说都是朝着最优的方向调整的。于是LMS算法也被称为随机梯度算法。

因此代价函数就成了：

E(w)=12(di−yi)2=12e2i

称为代价函数的瞬时值。
求偏导后即可得：

∂E∂w(n)=−x(n)e(n)

于是权值调整方式就是这样：

w(n+1)=w(n)+ηx(n)e(n)

η 同上为学习率参数。

R代码实现如下：

W = c(0,0) #初始化权值
eta = 1e-4 #学习率参数
n = 5 #进行5轮迭代

MSE = c() #均方根误差记录向量

for(t in 1:n){
  for(i in 1:N){
    e = d[i]-X[i,] %*% W
    W = W + e*X[i,] #修正权值

    E = d - X %*% W
    MSE = append(MSE,mean(E**2)) #计算并记录均方差
  }
}

这里学习率参数设为1e-4。可见在第一轮迭代中就已经收敛。因而在大量样本的数据中LMS的随机梯度方法相比前面几个方法更有性能优势。

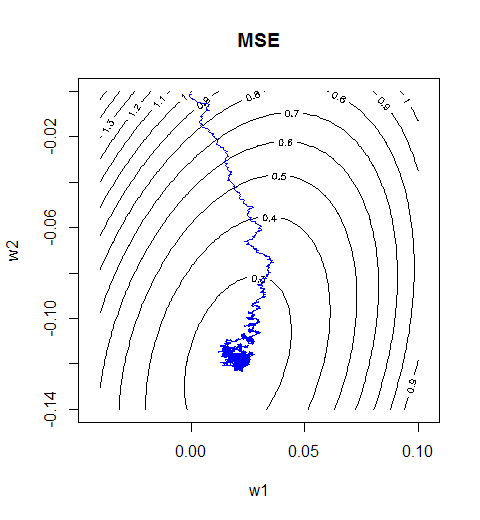
这里是权值向量调整的轨迹。尽管是边抖边走也最终还是走到了最优处，到了目的地之后就在原地做起了布朗运动。

学习率退火方案

限制LMS算法性能的一个因素就是学习率参数 η 被设为是固定的，更科学的方式应该是一开始大，后面越来越小。
于是就有人提出了一个形式，学习率参数应该随迭代次数变化： η(n)=cn 。这里c是一个常数。
但是要是c设得比较大，导致一开始的时候 η 太大咋办？于是就又提出了下面的方式：

η(n)=η01+n/τ

这里 η0 和 τ 都是可调常数。酱紫就可以在一开始的时候 η 不至于过大，而到了后期的时候接近于 cn 。这里 c=η0τ 。