记一下机器学习笔记 多层感知机的反向传播算法

《神经网络与机器学习》第4章前半段笔记以及其他地方看到的东西的混杂…第2、3章的内容比较古老预算先跳过。
不得不说幸亏反向传播的部分是《神机》里边人话比较多的部分，看的时候没有消化不良。

多层感知机

---

书里前三章的模型的局限都很明显，对于非线性可分问题苦手，甚至简单的异或都弄不了。于是多层感知机（也就是传说中的神经网络）就被发明了出来对付这个问题。

多层感知机就是由一系列的感知机，或者说神经元组成，每个神经元都接受若干的输入（树突）并产生一个输出（轴突）。
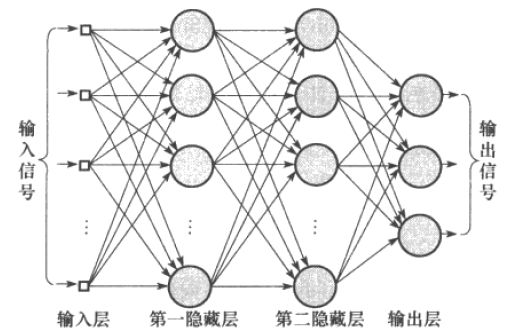
这些神经元被分成若干层，每一层的神经元的输出都被作为下一层的神经元的输入，直到最外一层。这时最外一层的输出就是整个神经网络的输出。

由于神经网络的神经元数目变多了，因此可存储的信息量也增加了，复杂度也提高了，可以解决一些更难的，感知机和LSM算法解决不了的问题。

神经网络工作原理

---

神经网络中，每个神经元都具备一系列权值参数和一个激活函数 ϕ(x) 。神经元的工作方式如下：
设一系列输入值为 x1,x2,x3,...,xm ，权值参数为 w0,w1,w2,w3,...,wm ， w0 为偏置项。

定义局部诱导域 v=w0+w1x1+w2x2+...+wmxm=wTx ，
其中 x=[1,x1,x2,x3,...,xm]T 为输入向量， w=[w0,w1,w2,w3,...,wm]T 为权值向量。

然后激活函数将局部诱导域 v 的值从整个实数集映射到某个需要的区间，作为神经元的输出值。比如激活函数为符号函数 sign() 的话，那么就会使得当 v 大于0时输出1，小于等于0时输出-1。
于是输出 y=ϕ(v)=ϕ(wTx)=ϕ(w0+w1x1+w2x2+...+wmxm)

激活函数的形式有很多，最常用的是 sigmoid 函数：

sigmoid(x)=11+e−ax

其中 a 为参数。它将输入值从实数集映射到0和1之间的范围内。

以及双曲正切函数：

tanh(x)=ex−e−xex+e−x

这个则是从实数集映射到-1到1之间。

---

于是整个神经网络的工作方式如下：

1. 首先有一系列输入 x1,x2,x3,...,xm ，加上作为偏置的1记为输入向量 x ， x=[1,x1,x2,x3,...,xm]T 。

2. 把 x 输入给网络第一层的每个神经元各自产生输出，设第一层有p个神经元，那么就会产生p个输出 y11,y12,y13,...,y1p （上标1表示其出自第一层神经元）。
   其中 y11=ϕ(v11)=ϕ(w1T1x) ， y12=ϕ(v12)=ϕ(w1T2x) ，…， y1p=ϕ(v1p)=ϕ(w1Tpx) ，以此类推。（ w12 表示第一层的第二个神经元的权值向量）
   这系列输出值组成第一层的输出向量 y1 。 y1=[y11,y12,...,y1p]T 。

3. 再把输出值向量像输入向量那样，前边带上1，组成第二层的输出向量 x1 。 x1=[1,y11,y12,...,y1p]T 。

4. 再然后就是把第一层的输出向量作为第二层的输入向量输入给第二层计算，产生第二层的输出，即：
   y21=ϕ(w2T1x1) ， y22=ϕ(w2T2x1) ，…
   以此类推。

就这样直到跑到最后一层神经元，往后已经没有其他神经元层了，那么这层神经元的输出就是整个神经网络的输出，于是这层被称为输出层。而往前的那些只是把输出传递给下一层的神经元层称为隐藏层。
这就是神经网络的信号的前向传播过程，称为前馈。

表示成矩阵的形式

---

实际应用中为了处理起来简便，上边的过程会表示为矩阵和向量的形式。
比如在第 l 层有n个神经元，上一层产生m个输出作为本层的输入，整层神经元的权值可以表示成这样的n行m+1列的矩阵形式：

Wl=⎡⎣⎢⎢⎢⎢⎢⎢wl10wl20wl30...wln0wl11wl21wl31wln1wl12wl22wl32wln2wl13wl23wl33wln3............wl1mwl2mwl3mwlnm⎤⎦⎥⎥⎥⎥⎥⎥

其中 Wl 为第 l 层权值矩阵， wlji 表示第 l 层的第 j 个神经元的对应于第 i 个输入值的权值，其中 wlj0 对应的为偏置项。
记 vl 为本层各个神经元输出产生的局部诱导域向量 [vl1,vl2,vl3,...,vln]T ，
记 yl 为本层各个神经元输出产生的输出向量 [yl1,yl2,yl3,...,yln]T ，
而 xl−1 为上一层的输出向量带上偏置项，也就是本层的输入向量 [1,yl−11,yl−12,yl−13,...,yl−1m]T ，
那么每一层的输出计算就可以记为如下简洁的形式：

vl=Wl⋅xl−1

yl=ϕ(vl)

然后往后的层也是如此：

xl=[1,yT1]T

vl+1=Wl+1⋅xl

yl+1=ϕ(vl+1)

反向传播（BP）算法

---

接下来就是多层感知机（神经网络）的学习策略。
在这里有必要了解梯度下降的原理，因为它是反向传播的基础。
神经网络也是跟感知机一样用的试错式学习。有监督学习情况下，给定一系列样本 x1,x2,...,xn 作为输入，每个样本都对应于一组期望的输出值，记为期望响应向量 d1,d2,...,dn 。
那么学习的目标就是让这神经网络对每个输入的样本，都产生出跟样本对应的期望响应尽可能接近的输出，最好一模一样。又或者说，尽可能地减小神经网络的输出值跟对应的期望响应之间的误差。

于是可以定义一个误差函数 E 作为衡量误差大小的指标，它受样本集、期望响应们和权值们的影响。然后因为数据集一般不会变，所以误差函数可认为自变量只有权值们，即

E=E(w)

这样子问题就变成了：找到一组权值 w 使得误差函数 E(w) 得最小值。
但是我们并不知道误差函数的全貌是什么样子，而且神经网络结构复杂，权值多如牛毛，要盲目得找来找到让误差函数最小的权值基本上是不可能的。

一个可行的办法就是从一个初始权值组 w0 开始，一步一步修正 w 来让误差函数 E(w) 一点一点得降到最小。
所以接下来梯度下降法就该出场了。

梯度下降

---

然后问题就可以变成这个说法：
在多维空间里，从一谷地边缘的某处 w0 出发，你并不知道谷底具体在哪，只知道所处位置周边的情况，如何走才能最终并最快地一步一步走到谷底？

当然是顺着坡最陡的方向往下走呗。

如果还记得高数的知识应该马上能想的出来：多元函数的梯度的方向就是坡最陡的方向，沿着这个方向函数值变化得最大。不过微积分规定梯度的正方向是让函数值增加的，所以应该顺着梯度相反的方向走，这样函数值降低得最快。
所以写出来就是：

Δw=−η∇E(w)

Δw 是权值向量每次的改变量， ∇ 是梯度算子，说白了就是对每个自变量求偏导值，求出来的向量取负便是最陡的下坡方向。
η 称为 学习率参数，可以理解为沿着这个方向踏出的一步的大小。
所以上式又可以写成：

Δw1=−η∂E∂w1,Δw2=−η∂E∂w2...

有了这个策略，就可以保证可以一步一步最终走到最低点了。这就是传说中的梯度下降（Gradient Descent）法。

当然这个只是最原始的梯度下降法，缺点很明显，你有可能最终走进的只是一个局部最低点，而不是全局最低点。

反向传播

---

先不聊反向传播是啥子，先拿梯度下降法来推导神经网络修改权值的公式。

首先将误差函数进行如下定义：

E(n)=12∑j=1ne2j(n)

其中 ej(n) 为第n个样本产生的第j个输出值的误差信号，即期望值减去输出值：

ej(n)=dj(n)−yj(n)

也就是说 E(n) 也就是第n个样本输入产生的输出层所有的输出的误差的平方和再除以2。除以2是为了后边求导时可以直接消掉。它也被称为全部瞬时误差能量。

有了具体的误差函数就可以直接求梯度了。
先看看输出层神经元的权值。

输出层神经元的反向传播公式

---

设 wlji 为第l层第j个神经元对输入向量中的第i个值的权值，l层为输出层，那么根据前文公式如下：

vlj=wlj0+wlj1x1+wlj2x2+...+wljmxm

ylj=ϕ(vlj)

ej=dj−ylj

E=12(e21+e22+e23+...+e2n)

然后让 E 对 wlji 求偏导，即：

∂E∂wlji=∂E(ej(ylj(vlj(wlji))))∂wlji

根据求导的链式法则，对上式可得：

∂E∂wlji=∂E∂ej⋅∂ej∂ylj⋅∂ylj∂vlj⋅∂vlj∂wlji

将上式右边每一项照着上边的公式求导求出来就会变成这个样子：

∂E∂wlji=ej⋅−1⋅ϕ′(vlj)⋅xi

其中 ϕ′ 为激活函数的导数。
整理一下，再带入梯度下降的原理公式得：

Δwlji=ηejϕ′(vlj)xi

定义 局域梯度 δj=ejϕ′(vlj) ，则又可以改写成：

Δwlji=ηδjxi

这就是输出层神经元的 反向传播公式。

接下来就是隐藏层。

隐藏层层神经元的反向传播公式

---

隐藏层咋办？依然是简单粗暴的解决办法——拿输出层输出的误差函数 E 对该层权值求梯度，只不过要更纠结一些。
先设这隐藏层后边就是输出层。此时输出层是第 s 层，隐藏层是第 l 层。
误差函数依然是：

E=12∑k=1ne2k

然后有：

ek=dk−ysk

上标 s 表示 ysk 为第 s 层即表层的第 k 个神经元的输出。
由于输入向量会被输入到该层所有神经元，因此对于输出层的每个神经元，都有：

ysk=ϕ(vsk)=ϕ(wsk0+wsk1xl1+wsk2xl2+...+wskjxlj+...)

由于第 l 层的输出被作为第 s 层的输入，于是对第 l 层第 p 个神经元有：

xlj=ylj

根据前文又有：

ylj=ϕ(vlj)=ϕ(wlj0+wlj1x1+wlj2x2+...+wljixi+...)

拿误差函数对本隐藏层的权值求导，依然根据链式求导法则：

∂E∂wlji=∑k=1m(∂E∂ej⋅∂ej∂ysk⋅∂ysk∂xlj)⋅∂xlj∂ylj⋅∂ylj∂wlji

得出了这么一坨东西。上面假设输出层有m个神经元。
然后就是仔细一项项求导了：

∑k=1m(∂E∂ej⋅∂ej∂ysk⋅∂ysk∂xlj)=∑k=1m(−ekϕ′(vsk)wskj)

∂xlj∂ylj∂ylj∂wlji=ϕ′(vlj)xi

综上，得

∂E∂wlji=−ϕ′(vlj)xi∑k=1m(ekϕ′(vsk)wskj)

这时你应该注意到了，上式右边的项 ekϕ′(vsk) 不就是第 s 层的局域梯度吗？
所以令 δk=ekϕ′(vsk) 为第 s 层第 k 个神经元的局域梯度，于是上式又可以表示成：

∂E∂wlji=−ϕ′(vlj)xi∑k=1m(δkwskj)

从而这就是隐藏层神经元的反向传播公式：

Δwlji=ηδk⋅xiδj=ϕ′(vlj)∑k=1m(δkwkj)

其中 δk 为后一层的第 k 个神经元的局域梯度。

从而可以推导出，每一层隐藏层神经元的局域梯度，等于其后一层所有神经元的局域梯度与其对本层神经元连接边的权值的乘积之和，乘上本层神经元激活函数对局部诱导域的导数。
xi 表示本层神经元的第 i 个输入值， η 为学习率参数。

如此一来，无论隐藏层有多深，每层隐藏层的权值修改都可以通过前一层的信息推导而得，而这一信息最终来源于输出层，输出层的信息又来源于误差信号。这就好像误差信号在从输出层开始，沿着各层间的连接边往后传播一样。
反向传播（Back Propagation）的说法就是这么来的。

这张图用来可视化误差的反向传播。

---

总结

神经元的调权公式的形式均为：

Δwlji=ηδjxi

即 学习率参数乘 局域梯度乘 该权值对应的输入值。

对于输出层，局域梯度 δj 计算公式为：

δj=ejϕ′(vlj)

即 误差信号乘 激活函数对局部诱导域的导数；
对于隐藏层则为：

δj=ϕ′(vlj)∑k=1m(δkwkj)

即 后一层所有神经元的 局域梯度以及 其与本层神经元各对应连接边的权值的 乘积之和，乘上 激活函数对本隐藏层神经元局部诱导域的导数。

其中公式已考虑了偏置项，此时 xi 的值为1。
实在懒得推的话，其实记住上面的三个公式也就好了。
简单吧。

总之：作为神经网络的标配，BP算法就是这么简单粗暴，一旦理解了就会觉得也没多少技术含量。其实这里推出来的只是BP算法的最原始的形式，有了它神经网络依然没有解决计算量大、容易陷入局部最优解和过拟合等一大堆问题，又比如学习率参数 η ，太大了怕不收敛，太小了又收敛得太慢，该如何取值就够让许多人发文了…

R语言实现

---

借助R原生的向量和矩阵处理功能可以方便简约地实现神经网络前馈和反向传播。
然后又是参考《神机》里边的例子，测试数据依然是双月牙数据集。双月牙的生成方式具体看上一篇关于感知机的文。

这里一上来就是间距为-4的线性不可分的双月牙：

点数依旧为2000。任务就是搞个神经网络把这两坨点分开。

参考《神机》，激活函数 ϕ(v) 为双曲正切函数，及其导数的R代码如下：

# 双曲正切函数及其导数
phi = function(v) tanh(v)
dphi = function(v) 1/(cosh(v)**2)

这个神经网络应有一层输入层（废话），一层隐藏层和一层输出层。
于是前向传播的R代码如下：

# 前向传播
# 由于R中起始下标为1，于是将偏置项放到向量后边
# x为输入向量，W1、W2分别为第一、二层的权值矩阵，v1、v2分别为第一、二层的局部诱导域向量，y1、y2分别为第一、二层的输出向量
FF = function(x){
  v1 = W1 %*% c(x,1)
  y1 = phi(v1)

  v2 = W2 %*% c(y1,1)
  y2 = phi(v2)

  return(y2)
}

定义神经网络参数。输入层节点数 m0 为2，隐藏层神经元数 m1 为20，输出层 m2 则为1，然后生成权值矩阵：

m0 = 2
m1 = 20
m2 = 1

# 权值矩阵
W1 = matrix(runif(m1*(m0+1),-0.5,0.5),nrow=m1, ncol=m0+1)
W2 = matrix(runif(m2*(m1+1),-0.5,0.5),nrow=m2, ncol=m1+1)

在这里权值矩阵初始值为-0.5到0.5之间的数。跟感知机不同，要是像感知机那样初始值全都设为0的话神经网络会跑不动…
另外根据《神机》的温馨提示，初始权值不能设太高，否则网络容易过早饱和，一饱和就跑不动了。

然后学习率参数 η 设为1e-1到1e-5的线性退火，设迭代次数n为50：

n = 50
eta = seq(1e-1,1e-5,length.out = n)

然后就是训练：

MSE=c() # 初始化均方根误差序列

for(j in 1:n){

  for(i in 1:N){
    # 前向传播
    x = dat[i,]
    v1 = W1 %*% c(x,b)
    y1 = phi(v1)

    v2 = W2 %*% c(y1,b)
    y2 = phi(v2)

    # 反向传播
    e2 = d[i] - y2
    delta2 = e2*dphi(v2)
    delta1 = dphi(v1)*(delta2*W2[1:m1])

    dW2 = (eta[j]*delta2) %*% c(y1,b)
    dW1 = (eta[j]*delta1) %*% c(x,b)

    W2 = W2 + dW2
    W1 = W1 + dW1
  } # 计算每一个样本

  # 计算均方根误差并记录
  e = d - apply(dat,1,FF)
  mse = sqrt(sum(e*e)/n)
  MSE[j]=mse
} # 迭代

最后是可视化运行结果：

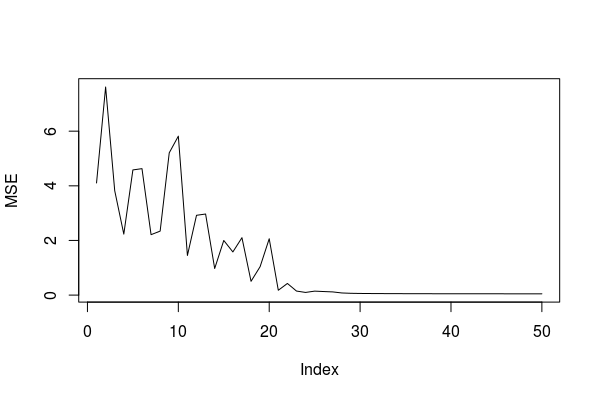
plot(MSE,type='l')

ty = sign(apply(dat,1,FF))
length(ty[ty!=d])/N #误分类率
ggplot()+geom_point(size=0.5,aes(x1,x2,color=factor(ty)))

开始跑数据…呃，结果是这样的：


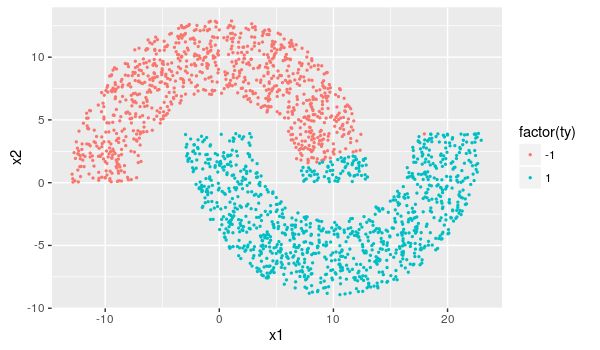
可见只有靠近原点周边的点被全部正确分类了，上半月牙有一小块分错了地。
误分类率为4%。

《神机》上面倒是声称这个网络可以百分百地正确分类，并且可以在第15回合左右收敛。然而并没有给出初始权值怎么搞，也没有给出还有没做过什么其他预处理的工序。

继续摸索…
为了画出神经网络分出来的边界，使用了ggplot2包的等高线函数geom_contour()。
具体方法是先创造一块若干排若干列的点集，然后所有点丢进神经网络跑出对应函数值，再使用等高线函数表现。

# 创造点集
qx = seq(min(x1),max(x1),length.out = 100)
qy = seq(min(x2),max(x2),length.out = 80)
q = merge(qx,qy)
names(q)=c('qx','qy')

# 求出每个点的函数
q$qz = apply(q,1,FF)

此时直接用ggplot2作出来的图是这样的：
qplot(data=q,qx,qy,color=qz)

已经可以看到分界轮廓了。接下来使用等高线函数画出边界：

op=q
op$x1=x1
op$x2=x2
op$y=sign(apply(dat,1,FF))
# 因为貌似ggplot2在用等高线图形函数的时候不支持同时画来自两个数据框的数据，只好蛋疼得重新搞了个数据框
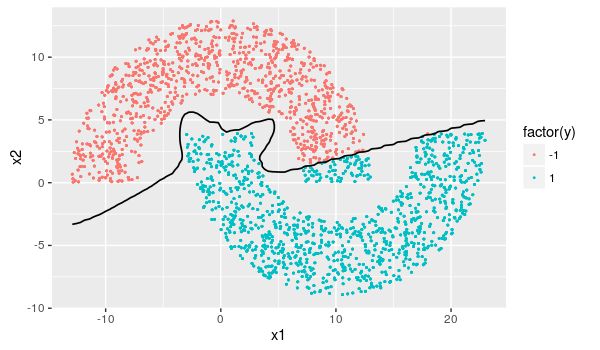
ggplot(data=op)+geom_point(aes(x=x1,y=x2,color=factor(y)), size=0.35)+
geom_contour(bins = 1,color='black',size=0.6,aes(x=qx,y=qy,z=qz))   

可发现神经网络只对于原点附近的数据敏感…
然后再往后翻终于发现《神机》的又一温馨提示：避免非0均值输入。
看来书里的样例是有经过标准化处理的。

接下来让样本均值为零，每个维度减去各自的均值：

x1=x1-mean(x1)
x2=x2-mean(x2)
# 重新生成数据集
dat = as.matrix(data.frame(x1,x2))

再跑，结果发现是这样子…

仍有3%的样本分类错了。

…

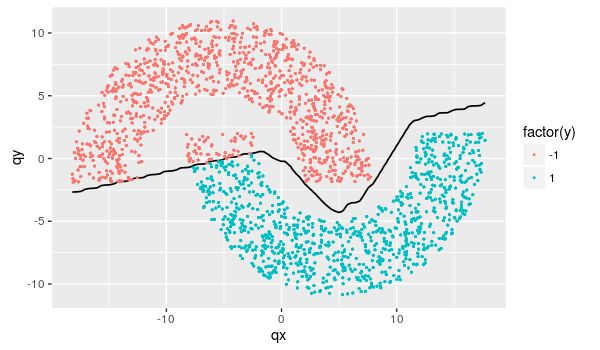
最后终于发现，隐藏层的初始权值-0.1到0.1间的随机数，输出层的初始权值设全部设为0.1，学习率参数退火改成5e-2到5e-6的时候，成功完成了分类…

虽然也没达到《神机》的15回合收敛。

总而言之，《神机》里边说神经网络与其说是一门技术，不如说是一门艺术，因为哪怕是有了BP算法，设初始权值这块也太™主观了…

---

下边是使用animation包配合ggplot2整的迭代过程动画，分别是月牙间距等于-4和-6的情况：