串_1 2016.4.27
一、串及串匹配
如何在字符串数据中,监测和提取以字符串形式给出的某一局部特性
这类操作都属于串模式匹配(string pattern matching)范畴,简称串匹配
一般地,即:
对基于同一字符表的任何文本串T(|T| = n)和模式串P(|P| = m):
判定T中是否存在某一子串与P相同
若存在(匹配),则报告该子串在T中的起始位置
串的长度n和m本身通常都很大,但相对而言n更大,即满足2 << m << n
比如,若:
T = "Now is the time for all good people to come"
P = "people"
则匹配的位置应该是29
二、暴力匹配(Brute‐force)
最直接最直觉的方法
构思:
bool Match(char* P, char *T) //暴力串匹配算法(版本1)
{
int n = strlen(T); //文本串长度
int m = strlen(P); //模式串长度
int i = 0, j = 0;
while (j < m && i < n) { //自左向右逐个比对字符
if (T[i] == P[j]) { //若匹配
++i; //则转到下一字符
++j;
} else { //文本串回退,模式串复位
i -= (j-1);
j = 0;
}
}
if (i-j < n-m+1) { //i - j < n - m + 1时匹配;否则失配
return true;
}
return false;
}bool Match(char* P, char *T) //暴力串匹配算法(版本2)
{
int n = strlen(T); //文本串长度
int m = strlen(P); //模式串长度
int i, j;
for (i=0; i
最好情况: 只经过一轮比对,即确定匹配
比对 = m = O(m)
最坏情况: 每轮都比对至P的末字符,且反复如此
每轮循环:比对 = m‐1(成功) + 1(失败) = m
循环次数 = n ‐ m + 1
一般 m ≪ n,故总体地,比对 = m × (n‐m+1) = O(n×m)
三、KMP算法
(1)构思
暴力算法应用于规模大的应用环境,很有必要改进
为此,不妨从分析以上最坏情况入手
稍加观察不难发现,问题在于这里存在大量的局部匹配:
每一轮的m次对比中,仅最后一次可能失配,文本串、模式串的字符指针都要回退,并从头开始下一轮尝试
实际上,这类重复的字符比对操作没有必要
既然这些字符在前一轮迭代中已经接受过比对并且成功,我们也就掌握了它们的所有信息
那么,如何利用这些信息,提高匹配算法的效率呢?
记忆 = 经验= 预知力
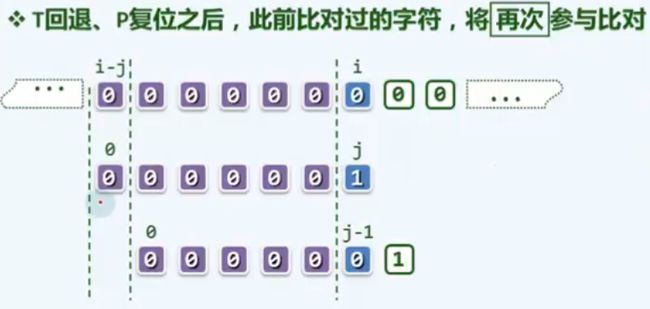
经过前一轮对比,我们已经清楚地知道,子串 T[i - j, i] 完全由 '0' 组成
记住这一性质我们便可预测出:
在回退之后紧接着的下一轮对比中,前 j - 1 次比对必然都会成功
因此,可直接 ”令 i 保持不变、j = j - 1 “ ,然后继续比对
如此,下一轮只需 1 次比对,共减少 j - i 次!
上述 ”令 i 保持不变、j = j - 1 “ 的含义,可理解为 “令 P 相对于 T 右移一个单元,然后从前一失配位置继续比对”:
实际上这一技巧可推而广之:
利用以往的成功比对所提供的信息(记忆),不仅可避免文本串字符指针的回退,而且可使模式串尽可能大跨度地右移(经验)
一般实例
再来考查一个更具一般性的实例
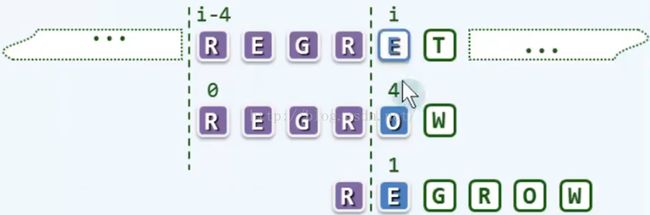
本轮对比进行到发现 T[i] = 'E' ≠ 'O' = P[4] 失配后,在保持 i 不变的同时,应将模式串 P 右移几个单元呢?
有必要逐个单元地右移吗?
不难看出,在这一情况下移动一个或两个单元都是徒劳的
事实上,根据此前的比对结果,此时必然有
T[i - 4, i) = P[0,4) = "REGR"
若在此局部能够实现匹配,则至少紧邻于 T[i] 左侧的若干字符均得到匹配
比如,当 P[0] 与 T[i - 1] 对齐时,即属于这种情况
进一步地,若注意到 i - 1 是能够如此匹配的最左侧位置,即可直接将 P 右移 4 - 1 = 3 个单元(等效于 i 保持不变,同时令 j = 1),然后继续比对
(2)next表
一般地,假设前一轮比对终止于 T[i] ≠ P[j]
按以上构思,指针 i 不必回退,而是将 T[i] 与 P[t] 对齐并开始下一轮比对
那么,t 准确地应该取作多少呢?
经过前一轮的比对,已经确定匹配的范围应为:
P[0, j) = T[i - j, i)
于是,若模式串 P 经适当右移之后,能够与 T 的某一(包含 T[i] 在内的)子串完全匹配,则一项必要条件就是:
P[0, t) = T[i - t, i) = P[j - t, j)
亦即,在 P[0, j) 中长度为 t 的真前缀,应与长度为 t 的真后缀完全匹配,故 t 必来自集合:
N(P, j) = { 0 ≤ t < j | P[0, t) = P[j - t, j) }
一般地,该集合可能包含多个这样的 t
但需要特别注意的是,其中具体由哪些 t 值构成,仅取决于模式串 P 以及前一轮对比的首个失配位置 P[j],而与文本串 T 无关!
若下一轮对比将从 T[i] 与 P[t] 的对比开始,这等效于将 P 右移 j - t 个单元,位移量与 t 成反比
因此,为保证 P 与 T 的对齐位置(指针 i )绝不倒退,同时又不致遗漏任何可能的匹配,应在集合 N(P, j) 中挑选最大的 t
也就是说,当有多个值得试探的右移方案时,应该保守地选择其中移动距离最短者
于是,若令
next[j] = max( N(p, j) )
则一旦发现 P[j] 与 T[i] 失配,即可转而将 P[ next[j] ] 与 T[i] 彼此对准,并从这一位置开始继续下一轮比对
既然集合 N(P , j) 仅取决于模式串 P 以及失配位置 j,而与文本串无关,作为其中的最大元素,next[j] 也必然具有这一性质
于是,对于任一模式串 P ,不妨通过预处理提前计算出所有位置 j 所对应的 next[j] 值,并整理为表格以便以后反复查询
亦即,将“记忆力”转化为“预知力”
(3)KMP算法
Knuth 和 Pratt 师徒,与 Morris 几乎同时发明了这一算法
他们稍后联合署名发表该算法,并以其姓氏首字母命名
这里,假定可通过 Build_Next() 构造出模式串 P 的 next 表
对照“暴力串匹配算法(版本1)”,只是在 else 分支对失配情况的处理手法有所不同,这也就是 KMP 算法的精髓所在
bool Match(char* P, char *T) //KMP主算法(待改进版)
{
Build_Next(P);
int n = strlen(T); //文本串长度
int m = strlen(P); //模式串长度
int i = 0, j = 0;
while (j < m && i < n) { //自左向右逐个比对字符
if (j < 0 || T[i] == P[j]) { //若匹配,或P已移出最左侧(两个判断的次序不可交换)
++i; //则转到下一字符
++j;
} else {
j = next[j]; //模式串右移(注意:文本串不用回退)
}
}
if (i-j < n-m+1) { //i - j < n - m + 1时匹配;否则失配
return true;
}
return false;
}(4)next[0] = -1
不难看出,只要 j > 0 则必有 0 ∈ N(P, j)
此时 N(P, j) 非空,从而可以保证“在其中取最大值”这一操作的确可行
但反过来,若 j = 0,则即便集合 N(P, j) 可以定义,也必是空集
此种情况下,又如何定义 next[j = 0] 呢?
若在某一轮对比中首对字符即失配,则应将 P 直接右移一个字符,然后启动下一轮对比
因此,不妨假想地在 P[0] 的左侧“附加”一个 P[-1] ,则该字符与任何字符都是匹配的
就实际效果而言,这一处理方法完全等同于“令 next[0] = -1”
巧妙的使用哨兵,可以
-简化代码
-统一理解
(5)next[j + 1]
那么,若已知 next[0, j] ,如何才能递推地计算出 next[j + 1]?
是否有高效方法?
由 next 表的功能定义,next[j + 1] 的下一候选者应该依次是 next[ next[j] ] + 1,
next[ next[ next[j] ] ] + 1,. . .
因此,只需反复用 next[t] 替换 t (即令 t = next[t]),即可按优先次序遍历以上候选者
一旦发现 P[j] 与 P[t] 匹配(含与 P[t = -1] 的通配),即可令 next[j + 1] = next[t] + 1
既然总有 next[t] < t,故在此过程中 t 必然严格递减
同时,即便 t 降至 0 ,亦必然会终止于通配的 next[0] = -1 ,而不致下溢
如此,该算法的正确性完全可以保证
(6)构造 next 表
void Build_Next(char* P) //构造模式串 P 的 next 表
{
int m = strlen(P);
int j = 0; //“主”串指针
int t = next[0] = -1; //模式串指针
while (j < m-1) {
if (t < 0 || P[j] == P[t]) { //匹配
++j;
++t;
next[j] = t; //此句可改进. . .
} else { //失配
t = next[t];
}
}
}可见,next 表的构造算法与 KMP 算法几乎完全一致
实际上按照以上分析,这一构造过程完全等效于模式串的自我匹配,因此两个算法在形式上的近似亦不足为怪
(7)性能分析
为此,请留意 KMP 算法中用作字符指针的变量 i 和 j
若令 k = 2i - j 并考查 k 在 KMP 算法过程中的变化趋势,则不难发现:
while 循环每迭代一轮,k 都会严格递增
实际上,对应于 while 循环内部的 if-else 分支,无非两种情况:
若转入 if 分支,则 i 和 j 同时加一,于是 k = 2i - j 必将增加
反之若转入 else 分支,则尽管 i 保持不变,但在赋值 j = next[j] 之后 j 必然减小,于是 k = 2i - j 也必然会增加
纵观算法的整个过程:
启动时有 i = j = 0,即 k = 0 ,算法结束时 i ≤ n 且 j ≥ 0,故有 k ≤ 2n
在此期间尽管整数 k 从 0 开始持续地严格递增,但累计增幅不超过 2n,故 while 循环至多执行 2n 轮
另外,while 循环体内部不含任何循环或调用,故只需 O(1) 时间
因此,若不计构造 next 表所需的时间,KMP 算法本身的运行时间不超过 O(n)
既然 next 表构造算法的流程与 KMP 算法并无实质区别,故按照上述分析可知,next 表的构造仅需 O(m) 时间
综上可知,KMP 算法的总体运行时间为 O(n + m)
(8)继续改进
尽管以上 KMP 算法已可保证线性的运行时间,但在某些情况下仍有进一步改进的余地
考查模式串 P = “000010”
在 KMP 算法过程中,假设前一轮对比因 T[i] = '1' ≠ '0' = P[3] 失配而中断
于是按照 next 表,接下来 KMP 算法将依次将 P[2]、P[1] 和 P[0] 与 T[i] 对准并做比对
这三次比对都报告“失配”
那么,这三次比对的失败结果属于偶然吗?
进一步地,这些比对能否避免?
实际上,即便说 P[3] 与 T[i] 的比对还算必要,后续的这三次比对却都是不必要的
实际上,它们的失败结果早已注定
只需注意到 P[3] = P[2] = P[1] = P[0] = '0' ,就不难看出这一点
既然经过此前的比对已经发现 T[i] ≠ P[3] ,那么继续将 T[i] 和那些与 P[3] 相同的字符做比对,既重蹈覆辙,更徒劳无益
记忆 = 教训= 预知力
就算法策略而言,引入 next 表的实质作用,在于帮助我们利用以往成功对比所提供的“经验”,将记忆力转化为预知力
然而实际上,此前已进行过的比对还远不止这些,确切地说还包括那些失败的比对----作为“教训”,它们同样有益,但可惜此前一直被忽略了
以往所做的失败比对,实际上已经为我们提供了一条极为重要的信息---- T[i] ≠ P[3] ---- 可惜我们却未能有效地加以利用
原算法之所以会执行后续三次本不必要的比对,原因在于未能充分汲取教训
改进
为把这类“负面”引入 next 表,只需将集合 N(P, j) 的定义修改为:
N(P, j) = { 0 ≤ t < j | P[0, t) = P[j - t, j) 且 P[t] ≠ P[j] }
也就是说,除“对应于自匹配长度”以外,t 只有还同时满足“当前字符对不匹配”的必要条件,方能归入集合 N(P, j) 并作为 next 表项的候选
void Build_Next(char* P) //构造模式串 P 的 next 表(改进版本)
{
int m = strlen(P);
int j = 0; //“主”串指针
int t = next[0] = -1; //模式串指针
while (j < m-1) {
if (t < 0 || P[j] == P[t]) { //匹配
++j;
++t;
next[j] = (P[j] != P[t] ? t : next[t]); //注意此句与未改进之前的区别
} else { //失配
t = next[t];
}
}
}改进后的算法与原算法的唯一区别在于,每次在 P[0, j) 中发现长度为 t 的真前缀和真后缀相互匹配之后,还需进一步检查 P[j] 是否等于 P[t]
唯有 P[j] ≠ P[t] 时,才能将 t 赋予 next[j],否则,需转而代之以 next[t]
改进后的 next 表的构造算法同样只需 O(m) 时间
BJFU OJ 1553 易彰彪的一张表
#include
#include
#include
using namespace std;
const int maxn = 30 + 10;
char T[maxn * maxn];
char P[maxn * maxn];
int next[maxn * maxn];
int n, m;
int T_len, P_len;
void Build_Next(char* P);
bool Match(char* P, char *T);
int main()
{
// freopen("in.txt", "r", stdin);
while (scanf("%d%d", &n, &m) != EOF) {
T_len = n*m;
for (int i=0; i>T[i];
}
strlwr(T);
scanf("%s", P);
P_len = strlen(P);
strlwr(P);
if (Match(P, T)) {
printf("YES\n");
} else {
printf("NO\n");
}
}
return 0;
}
void Build_Next(char* P)
{
int j = 0;
int t = next[0] = -1;
while (j < P_len-1) {
if (t < 0 || P[j] == P[t]) {
++j;
++t;
next[j] = (P[j] != P[t] ? t : next[t]);
} else {
t = next[t];
}
}
}
bool Match(char* P, char *T)
{
Build_Next(P);
int i = 0, j = 0;
while (j < P_len && i < T_len) {
if (j < 0 || T[i] == P[j]) {
++i;
++j;
} else {
j = next[j];
}
}
if (i-j < T_len-P_len+1) {
return true;
}
return false;
} HDU 1711 Number Sequence
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
int a[1000010];
int b[10010];
int N, M;
int Next[10010];
void Build_Next(void);
int Match(void);
int main()
{
#ifdef __AiR_H
freopen("in.txt", "r", stdin);
#endif // __AiR_H
int T;
scanf("%d", &T);
while (T--) {
scanf("%d%d", &N, &M);
for (int i = 0; i < N; ++i) {
scanf("%d", &a[i]);
}
for (int i = 0; i < M; ++i) {
scanf("%d", &b[i]);
}
printf("%d\n", Match());
}
return 0;
}
void Build_Next(void)
{
int i = 0;
int t = Next[0] = -1;
while (i < M-1) {
if (t < 0 || b[i] == b[t]) {
++i;
++t;
Next[i] = (b[i] != b[t] ? t : Next[t]);
} else {
t = Next[t];
}
}
}
int Match(void)
{
Build_Next();
int i = 0, j = 0;
while (i < N && j < M) {
if (j < 0 || a[i] == b[j]) {
++i;
++j;
} else {
j = Next[j];
}
}
if (i-j < N-M+1) {
return (i-M+1);
}
return -1;
}