曲线分类-特征提取(一)

一种异常检测算法很难满足所有的业务类型曲线。若想提高智能告警的准确度，有必要对不同 曲线进行分类，以便于针对不同曲线，应用不同的异常检测算法。那么一条曲线，到底包含了哪些信息，可以帮助我们进行特征提取呢？

数据描述

数据每分钟一个点，一天1440个数据点，每天为一个周期，共7天数据。
测试数据为monitor数据，视图4180,属性231960.

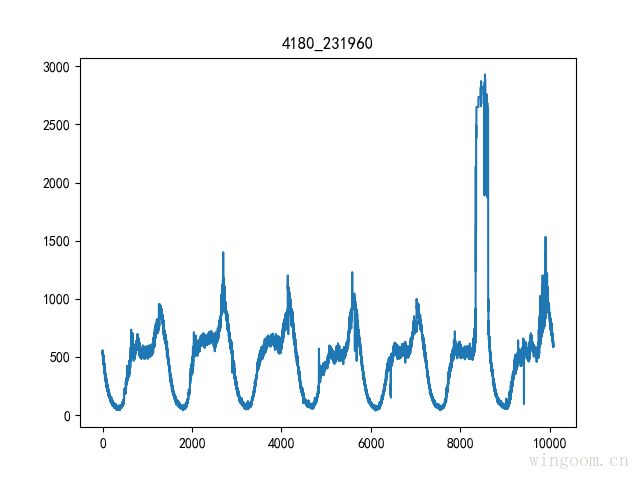
数据去噪

常用的去噪方法有：3-σ去噪、移动中位数去噪。

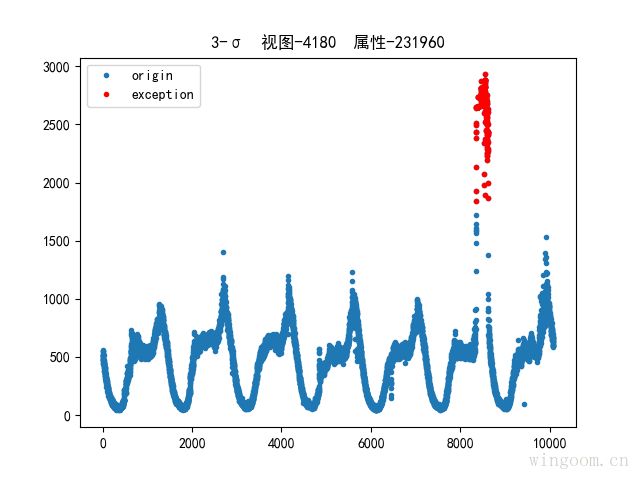
3-σ去噪

数据点与均值相差超过3个标准差，则认为为噪点

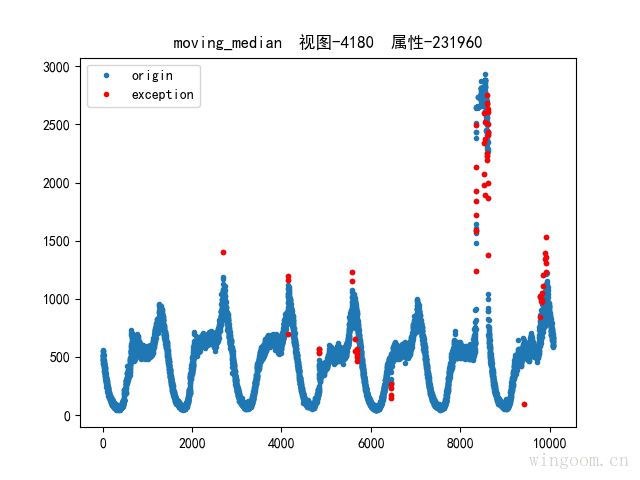
移动中位数去噪

用中位数代替均值，用中位数偏差代替标准差，避免极端异常值的影响。通过移动分段中位数，增强局部异常点的探测。

import numpy as np
import pandas as pd
def median_noise_filter(df_data, threshold=15,rolling_median_window=50):
    exceptions = pd.Series()
    df_data['median'] = df_data['value'].rolling(window=rolling_median_window, center=True).median().fillna(method='bfill').fillna(
        method='ffill')
    difference = np.abs(df_data['value'] - df_data['median'])
    median_difference = np.median(difference)
    if median_difference != 0:
        s = difference / float(median_difference)
        exceptions = s[s > threshold]
    return exceptions

移动中位数去噪需要选择合适的滑动窗口和偏差阈值参数。3-σ简单直接，但会受到极端值的影响

噪点填充

噪点填充为前一个和后一个正常点的均值

数据标准化(归一化)

将数据按比例缩放，去除数据的单位限制，将其转化为无量纲的纯数值，专注于曲线的形状识别，而不关心曲线上点数值的大小。

max-min标准化

对原始数据的一种线性变换，使原始数据映射到[0-1]之间，指将原始数据的最大值映射成1，是最大值归一化

x∗=x−minmax−min x ∗ = x − m i n m a x − m i n

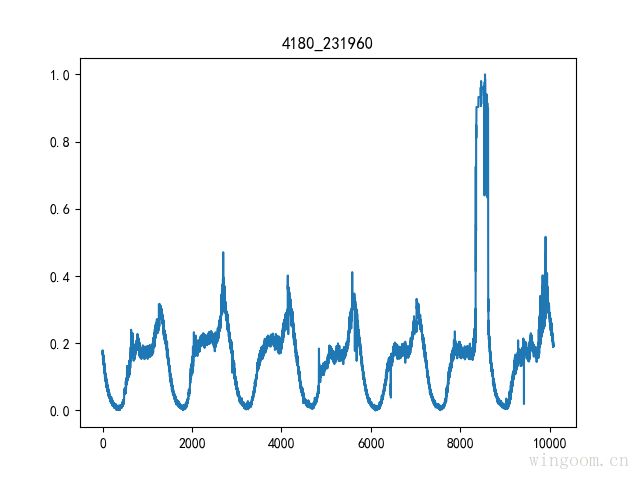
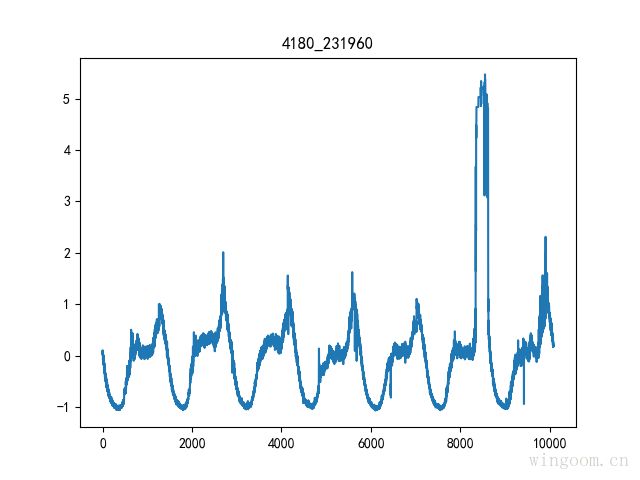
z-score标准化

根据原始数据的均值和标准差进行标准化,经过处理后的数据符合标准正态分布，即均值为0，标准差为1.本质上是指将原始数据的标准差映射成1，是标准差归一化。曲线数值表示该点与均值相差的标准差的数据量：

x∗=x−μσ x ∗ = x − μ σ

曲线值反映了数据点与均值相差的标准差个数。

统计特征

中心位置

借由中心位置，可以知道数据的一个平均情况。数据的中心位置可分为均值（Mean），中位数（Median），众数（Mode）

• 均值：表示统计数据的一般水平。受到极端值影响
• 中位数：在 n 个数据由大到小排序后，位在中间的数字，不受极端值影响
• 众数：一组数据中出现次数最多的数据值，不受极端值影响、非数值性数据同样适用

发散程度

数据的发散程度可用极差或全距（R）、方差（Var）、标准差（STD）、变异系数（CV）来衡量.

R=xmax−xmin R = x m a x − x m i n

Var(X)=∑Ni=1(xi−μ)2N V a r ( X ) = ∑ i = 1 N ( x i − μ ) 2 N

STD=Var−−−−√ S T D = V a r

CV=STDMean C V = S T D M e a n

零值率

零值所占的比率，需要在max-min标准化前提前该特征

波动率

波动率定义为7天波动率的中位数。
每天的波动率定义为该天数据标准化后的90分位值-10分位值：

wave_rateday=quantile(xnorm,0.9)−quantile(xnorm,0.1) w a v e _ r a t e d a y = q u a n t i l e ( x n o r m , 0.9 ) − q u a n t i l e ( x n o r m , 0.1 )

或者可以直接采用 wave_rate=quantile(x,0.9)−quantile(x,0.1)+1quantile(x,0.1)+1 w a v e _ r a t e = q u a n t i l e ( x , 0.9 ) − q u a n t i l e ( x , 0.1 ) + 1 q u a n t i l e ( x , 0.1 ) + 1

偏度（Skewness）

偏度（偏态）是不对称性的衡量。正态分布的偏度是0，表示左右完美对称。右偏度为正，左偏度为负.
Skewness 定义为：

S=∑nt=1(xt−μ)3nσ3 S = ∑ t = 1 n ( x t − μ ) 3 n σ 3

其中 μ μ 为均值， σ σ 为标准差，实际计算中，通过其样本值代替 μ μ ， σ3 σ 3

峰度（kurtosis）

峰度（Kurtosis）衡量数据分布相对于正态分布，是否更尖或平坦。高峰度数据在均值附近有明显峰值，下降很快并且有重尾（heavy tails）。低峰度在均值附近往往为平坦的顶部。
峰度（Kurtosis）定义为：

K=∑nt=1(xt−μ)4nσ4−3 K = ∑ t = 1 n ( x t − μ ) 4 n σ 4 − 3

其中 μ μ 为均值， σ σ 为标准差，实际计算中，通过其样本值代替 μ μ ， σ4 σ 4 .
该计算值也称为超值峰度（excess kurtosis），正态分布的峰度为3。公式减3，是为了修正使正态分布的峰度为0。
K>0，称为尖峰态（leptokurtic）
K<0，称为低峰态（platykurtic）

参考：

[1] Tsfresh. https://tsfresh.readthedocs.io/en/latest/text/introduction.html
[2] A Scalable Method for Time Series Clustering. https://www.researchgate.net/publication/228894373_A_scalable_method_for_time_series_clustering
[3] 矩、峰度、偏度. http://yaoyao.codes/math/2014/09/04/moment-expectation-variance-skewness-and-kurtosis