二分图的最大匹配

（一） 需求和规格说明

（1）问题描述：

写出求一个二分图的最大匹配的算法，并用于解决下面的问题。

第二次世界大战时期，英国皇家空军从沦陷国征募了大量外籍飞行员。由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的2 名飞行员，其中1名是英国飞行员，另1 名是外籍飞行员。在众多的飞行员中，每一名外籍飞行员都可以与其他若干名英国飞行员很好地配合。如何选择配对飞行的飞行员才能使一次派出最多的飞机。对于给定的外籍飞行员与英国飞行员的配合情况，试设计一个算法找出最佳飞行员配对方案，使皇家空军一次能派出最多的飞机。

（2）编程任务：

对于给定的外籍飞行员与英国飞行员的配合情况，编程找出一个最佳飞行员配对方案，使皇家空军一次能派出最多的飞机。

数据输入：

由文件input.txt提供输入数据。文件第1 行有2 个正整数m和n。n是皇家空军的飞行员总数（n<100）；m是外籍飞行员数。外籍飞行员编号为1~m；英国飞行员编号为m+1~n。接下来每行有2 个正整数i和j，表示外籍飞行员i可以和英国飞行员j配合。文件最后以2个-1 结束。

结果输出：

程序运行结束时，将最佳飞行员配对方案输出到文件output.txt 中。第1 行是最佳飞行员配对方案一次能派出的最多的飞机数M。接下来M 行是最佳飞行员配对方案。每行有2个正整数i和j，表示在最佳飞行员配对方案中，飞行员i和飞行员j 配对。

如果所求的最佳飞行员配对方案不存在，则输出‘No Solution!’。

（3）输入输出示例

输入文件示例：

input.txt    

5   10        

1   7

1   8

2   6

2   9

2   10

3   7

3   8

4   7

4   8 

5   10

-1  -1

 

输出文件示例：

output.txt

4

1  7

2  9

3  8

5  10

（二） 设计

先用邻接矩阵存储，然后利用匈牙利算法求解，用类似深度优先搜索的方法找出增广路，然后依次进行取反，即可得出匹配方案。其中，保存各结点匹配关系时，定义了一个矩阵pipei[max]，例如：pipei[k]=i，即k结点与i结点相匹配。

增广路的定义（也称增广轨或交错轨）：

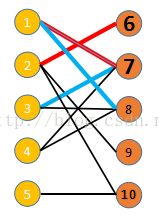
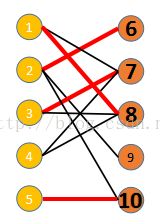
若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边（即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。例如，下图中蓝色路径③⑦①⑧为相对于已匹配边①⑦的增广路。

                                                       

                                   图 1 加粗红色边表示已匹配边，加粗数字表示已标记结点

 

由增广路的定义可以推出下述三个结论：

1－P的路径个数必定为奇数，第一条边和最后一条边都不属于M且整条路径上没有重复的点；

2－将M和P进行取反操作可以得到一个更大的匹配M’；

3－M为G的最大匹配当且仅当不存在M的增广路径。

算法轮廓：

⑴置M为空；

⑵找出一条增广路径P，通过取反操作获得更大的匹配M’代替M；

⑶重复⑵操作直到找不出增广路径为止。

 

                       图表 1  程序运行步骤详解

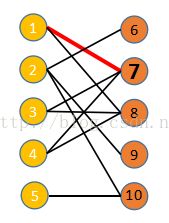
第一步	依次从各个未访问结点寻找增广路，例如：刚开始时从①结点找到一条长度为1的增广路①⑦，将⑦结点标记为已访问，并将⑦所匹配的结点①计入数组中保存，然后进行取反，则可派出飞机架数由0变为1，具体情况如右图：
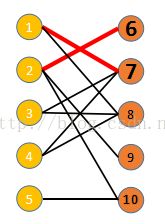
第二步	从②结点找到一条增广路②⑥，将⑥结点标记，并将⑥结点所匹配的结点②计入数组中保存，然后进行取反，可派出飞机架数由1变为2，得右图：
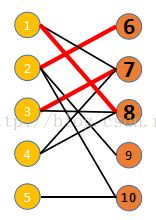
第三步	从③结点找增广路时，找到的增广路为③⑦①⑧，将⑧结点标记，然后取反，得到⑦结点匹配的点为③，⑧结点匹配的点为①，可派出飞机架数由2变为3，如右图所示：
第四步	从④结点找增广路时发现这条增广路经会陷入死循环，即:④⑦③⑧①⑦③，此时，结点③在增广路中出现第二次，由判断条件visited_v2直接结束循环，所以此时匹配方式没有发生变化。
第五步	从⑤结点找到增光路径⑤⑩，将结点⑩标记，并将结点⑩对应的结点⑤存入数组，取反，可派出飞机架数由3变为4，最终得到右图所示的匹配方案，即：①⑧；②⑥；③⑦；⑤⑩

 

（三） 用户手册

程序运行时，首先提示输入外籍飞行员数以及皇家空军的飞行员总数（<100）。

然后提示输入各飞行员间的对应关系，输入时以“-1 -1”作为输入结束标志。

（四） 调试及测试

直接输入各组数据即可。

（五）进一步改进

找到在派出最多的飞机架数的前提下所有的飞行员匹配方案，对于解决现实生活中的问题时更有实际意义。比如：如果某位飞行员临时有急事，不能工作，可以利用方案B及时解决这个问题。当然，再重新运行一下程序，只是输入时把这位临时有事的飞行员结点不输入也可以解决这一问题。另外可以尝试带权二分图的最大匹配，用权值代表所匹配的人对这项工作的热切程度或熟练度。

（六）附录¾¾源程序

#include "iostream"
#include "cstring"
#include "cstdio"
#include "algorithm" 
#define max 101
using namespace std;
int map[max][max]; //存储图
int pipei[max]; //记录V2中的点所匹配的点的编号
bool visited_v2[max]; //记录V2中的每个点是否被搜索过
int jieguo[max];//对最终的结果进行排序 
int m,n;// 外籍飞行员数以及皇家空军的飞行员总数
//图的存储（邻接矩阵）
int graph()
{
	cout<<"请依次输入外籍飞行员数以及皇家空军的飞行员总数（<100）：";
	cin>>m>>n;
	int v1,v2;
	cout<<"请输入各飞行员间的对应关系（以-1 -1作为结束输入标志）：" <>v1>>v2&&v1!=-1&&v2!=-1)
		map[v1][v2]=1;
	return 0;
}
//判断是否存在增广路
bool findpath(int i)
{
	for(int j=m+1;j<=n;j++)
	{
		if(map[i][j]&&!visited_v2[j]/*保证一个节点只经过一次*/)
		{
			visited_v2[j]=true;
			if(pipei[j]==0||findpath(pipei[j]))
			{
				pipei[j]=i;
				return true;
			}
		}
	}
	return false;
}
//对最终结果进行排序
void sort_jieguo() 
{
	int i=0;
	for(int k=m+1;k<=n;k++)
	    if(pipei[k])
	    {
	        jieguo[i]=pipei[k];//找到最终参加匹配的前半部分数存入数组中 
			i++; 
		} 
	sort(jieguo,jieguo+i);
	for(int j=0;j