二分图详解----匈牙利算法+km算法+ Gale-Shapley---婚姻匹配算法算法+例题
先介绍一下基本概念
以下基本概念转自其他的博客,不是原创
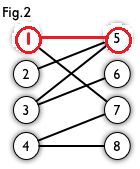
二分图:简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。准确地说:把一个图的顶点划分为两个不相交集 和 ,使得每一条边都分别连接 、 中的顶点。如果存在这样的划分,则此图为一个二分图。二分图的一个等价定义是:不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰,我们以后都把它画成图 2 的形式。
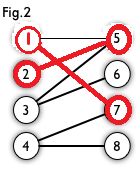
匹配:在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配
![]()
![]()
![]()
![]()
我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点,其他顶点为未匹配点;1-5、4-7为匹配边,其他边为非匹配边。
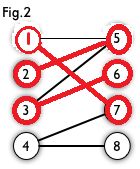
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
上述是基本概念,接下来讲一下为匈牙利算法服务的一些概念
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。![]()
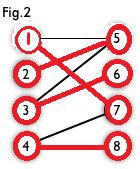
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。例如,图 5 中的一条增广路如图 6 所示(图中的匹配点均用红色标出):
![]()
增广路有一个重要特点:非匹配边比匹配边多一条。因此,研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目比原来多了 1 条。其实,如果交替路以非匹配点结束的,那么这条交替路就是一条增广路
我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理)。匈牙利算法正是这么做的
接下来开始讲匈牙利算法
算法的基本思想:
基本思想:通过寻找增广路,把增广路中的匹配边和非匹配边的身份交换,这样就会多出一条匹配边,直到找不到增广路为止。
代码如下:
#include
#define MAXN 9999
using namespace std;
int nx,ny;//nx表示二分图左边顶点的个数,ny表示二分图右边顶点的个数
int m;//m代表边的条数
int cx[MAXN],cy[MAXN];//如果有cx[i]=j,则必有cy[j]=i,说明i点和j点能够匹配
int x,y;//x点到y点有边
int e[MAXN][MAXN];//邻接矩阵
int visited[MAXN];//标记数组,标记的永远是二分图右边的顶点
int ret;//最后结果
int point(int u)//这个函数的作用是寻找增广路和更新cx,xy数组,如果找到了增广路,函数返回1,找不到,函数返回0。
{
for(int v=1;v<=ny;v++)//依次遍历右边的所有顶点
{
if(e[u][v]&&!visited[v])//条件一:左边的u顶点和右边的v顶点有连通边,条件二:右边的v顶点在没有被访问过,这两个条件必须同时满足
{
visited[v]=1;//将v顶点标记为访问过的
if(cy[v]==-1||point(cy[v]))//条件一:右边的v顶点没有左边对应的匹配的点,条件二:以v顶点在左边的匹配点为起点能够找到一条增广路(如果能够到达条件二,说明v顶点在左边一定有对应的匹配点)。
{
cx[u]=v;//更新cx,cy数组
cy[v]=u;
return 1;
}
}
}
return 0;//如果程序到达了这里,说明对右边所有的顶点都访问完了,没有满足条件的。
}
int main()
{
while (cin>>m>>nx>>ny)
{
memset(cx,-1,sizeof(cx));//初始化cx,cy数组的值为-1
memset(cy,-1,sizeof(cy));
memset(e,0,sizeof(e));//初始化邻接矩阵
ret=0;
while (m--)//输入边的信息和更新邻接矩阵
{
cin>>x>>y;
e[x][y]=1;
}
for(int i=1;i<=nx;i++)//对二分图左边的所有顶点进行遍历
{
if(cx[i]==-1)//如果左边的i顶点还没有匹配的点,就对i顶点进行匹配
{
memset(visited,0,sizeof(visited));//每次进行point时,都要对visited数组进行初始化
ret+=point(i);//point函数传入的参数永远是二分图左边的点
}
}
cout< 分析一下poiint函数是如何运行的,通过上图分析,第一次以1顶点为起点进入point(1)函数,然后5号顶点满足条件,更新cx[1],cy[5],返回1。此时1-->5这条边为匹配边,1号,5号顶点为匹配顶点
然后以2顶点为其实点进入point(1)函数,然后访问到5号节点,然后以5号节点的匹配点1号节点为起始点再次进入point(2)函数,找到了7号点,这时说明找到了增广路,然后更新cx[1],cy[7],然后返回1,更新cx[2],cy[5],返回一,函数结束。
然后以3号顶点为起始点进入point(1)函数,然后访问到5号节点,然后以5号节点的匹配点2号节点为起始点再次进入point(2)函数,找不到点了,返回0,到达point(1)函数,继续访问其他的节点。然后访问到6号顶点,满足条件,更新cx[3],cy[6],返回一,函数结束。
然后以4号顶点为起始点进入point(1)函数,然后访问到7号节点,然后以7号节点的匹配点1号节点为起始点再次进入point(2)函数,然后找到5号节点,然后以5号节点的匹配点2号节点为起始点再次进入point(3)函数,找不到点了,返回0,到达point(2)函数,继续访问其他的节点,没有点了,返回0,到达point(1)函数,继续访问其他的节点,到达了8号节点,满足,然后更新cx[4],cy[8],返回一,函数结束。
上图就是找到的所有的匹配边。
KM算法:
关于km算法写的比较好的两篇文章:
https://www.cnblogs.com/wenruo/p/5264235.html
https://www.cnblogs.com/logosG/p/logos.html?tdsourcetag=s_pcqq_aiomsg
我学km算法就是通过这篇博客学的,里面讲的很清楚,我就不详细讲了,直接上代码吧
代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define INT 9654234
#define mod 1000000007
typedef long long ll;
using namespace std;
const int MAXN = 305;
int N;
int ex_gir[MAXN];//每个妹子的期望值
int ex_boy[MAXN];//每个男生的期望值
bool vis_gir[MAXN];//记录每一轮匹配过的女生
bool vis_boy[MAXN];//记录每一轮匹配过的男生 每进行新的一轮,都要重新初始化这两个数组
int match[MAXN];//match[i]代表和i男生匹配的女生的编号
int slack[MAXN];//slack[i]代表i男生如果要获得女生的芳心,至少需要增加的期待值
int love[MAXN][MAXN];//记录每个妹子和男生的好感度
bool dfs(int gir)//dfs函数求的是编号为gir的女孩能否匹配到男生,如果能,返回true,否则,返回false
{
vis_gir[gir]=true;//标记
for(int i=1;i<=N;i++)
{
if(vis_boy[i])//我们规定每次匹配对于某个男生只访问一遍,如果先前访问过了,就换个男生
continue ;
int gap=ex_gir[gir]+ex_boy[i]-love[gir][i];
if(gap==0)//如果这个条件满足,说明编号为gir女孩和编号为i的男孩可能能够匹配成功
{
vis_boy[i]=true;//标记
if(match[i]==-1||dfs(match[i]))//如果这两个条件满足其中一个,说明编号为gir女孩和编号为i的男孩匹配成功
{
match[i]=gir;
return true;
}
}
else
slack[i]=min(slack[i],gap);//如果gap不等于0,说明当前状态编号为gir女孩和编号为i的男孩不可能匹配成功,更新slack[i]。
}
return false;
}
int km()
{
memset(match,-1,sizeof(match));
memset(ex_boy,0,sizeof(ex_boy));
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++)
ex_gir[i]=max(love[i][j],ex_gir[i]);//初始化ex_gir数组
for(int i=1;i<=N;i++)
{
fill(slack,slack+N+1,INT);
while (1)//这个while循环结束的条件是直到让编号为i的女生找到可以匹配的男生后
{
memset(vis_gir,false,sizeof(vis_gir));
memset(vis_boy,false,sizeof(vis_gir));
if(dfs(i))//如果这个条件满足,说明编号为i的女生找到了匹配的男生,换下一个女生,如果这个条件不满足,说明这个女生没有匹配到男生,让这个女生降低期望值后继续匹配
break ;
int t=INT;
for(int j=1;j<=N;j++)//寻找在这一轮匹配中没有匹配到的男生如果要获得女生芳心所需要增加的期待值的最小值
if(!vis_boy[j])
t=min(t,slack[j]);
for(int i=1;i<=N;i++)//让在这一轮匹配中匹配过的女生的期待值减小,匹配过的男生的期待值增加
{
if(vis_gir[i])
ex_gir[i]-=t;
if(vis_boy[i])
ex_boy[i]+=t;
else
slack[i]-=t;//因为有些女生的期待值减小了,所以这一轮没有被匹配过的男生得到女生的芳心所需要增加的期待值就变小了,所以slack数组中的相应的值要变小
}
}
}
int res=0;//计算好感和
for(int i=1;i<=N;i++)
res+=love[match[i]][i];
return res;
}
int main()
{
cin>>N;
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++)
cin>>love[i][j];
cout<
Gale-Shapley---婚姻匹配算法算法
参考文献:
https://blog.csdn.net/Air_hjj/article/details/70828937
https://blog.csdn.net/lc_miao/article/details/78116064
这两篇文章讲的很详细,直接上代码。
代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
#define MAXN 1000
typedef long long ll;
using namespace std;
int ManArray[MAXN][MAXN],GirArray[MAXN][MAXN];//ManArray[i][j]代表编号为i的男生的第j位心仪女生是几号,GirArray[i][j]代表编号为i的女生的第j位心仪男生是几号
int Man[MAXN],Gir[MAXN];//Man[i]代表i号男生所匹配到的女生是几号,Gir[i]代表i号女生所匹配到的男生是几号
int ManStarPos[MAXN];//ManStarPos[i]代表i号男生现在匹配到的女生是他心目中的第几号心仪女生
int n;
stack < int >q;//始终存放没有匹配成功的男生的编号
int GetPositionFromLaday(int GirI,int ManI)//这个函数求的是编号为ManI的男生在编号为GirI的女生的心中的排名顺序
{
for(int i=0;i>n;
memset(Man,-1,sizeof(Man));//初始化这三个数组
memset(Gir,-1,sizeof(Gir));
memset(ManStarPos,0,sizeof(ManStarPos));
for(int i=0;i>ManArray[i][j];
for(int i=0;i>GirArray[i][j];
for(int i=0;i
二分图例题:
关于二分图的题目,难点在于建图上面,如果图建好了,剩下的就是套用模板了。所以,做二分图的题目,关键在于建图,关于如何建图,推荐一篇文章:
https://wenku.baidu.com/view/63c1a01655270722192ef7c3.html
例题一:【HDU-1083】
http://acm.hdu.edu.cn/showproblem.php?pid=1083
题意:
有p门的课,每门课都有若干学生,现在要为每个课程分配一名课代表,每个学生只能担任一门课的课代表,如果每个课都能找到课代表,则输出"YES",否则"NO"。
思路:
二分图的模板题,我们定义课程在左边,学生在右边,直接套模板,最后判断一下所有的课程是否都有课代表就行了,
代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
#define MAXN 400
typedef long long ll;
using namespace std;
int t;
int x,y;
int LinJie[MAXN][MAXN];
int nx[MAXN],ny[MAXN];
int visited[MAXN];
bool point(int u)
{
for(int v=1;v<=y;v++)
{
if(LinJie[u][v]&&!visited[v])
{
visited[v]=1;
if(ny[v]==-1||point(ny[v]))
{
nx[u]=v;
ny[v]=u;
return 1;
}
}
}
return 0;
}
int main()
{
cin>>t;
while(t--)
{
memset(LinJie,0,sizeof(LinJie));
memset(nx,-1,sizeof(nx));
memset(ny,-1,sizeof(ny));
cin>>x>>y;
for(int i=1;i<=x;i++)
{
int v,z;
cin>>v;
for(int j=0;j>z;
LinJie[i][z]=1;
}
}
for(int i=1;i<=x;i++)
{
if(nx[i]==-1)
{
memset(visited,0,sizeof(visited));
point(i);
}
}
int c=0;
for(int i=1;i<=x;i++)
{
if(nx[i]==-1)
{
cout<<"NO"<
例题二:POJ【3020】
题意:
一个矩形中,有N个城市’*’,现在这n个城市都要覆盖无线,若放置一个基站,那么它至多可以覆盖相邻的两个城市。
问至少放置多少个基站才能使得所有的城市都覆盖无线?
思路:
这个题的题解:
https://blog.csdn.net/lyy289065406/article/details/6647040
代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
#define MAXN 50
#define maxn 2500
typedef long long ll;
using namespace std;
int t,n,m;
int root[MAXN][MAXN];//root数组存的是题目给定的数据
int LinJie[maxn][maxn];//LinJie数组存的是拆点完成后得到的二分图的一些信息
int nx[maxn],ny[maxn];//匈牙利算法所用到的数组
int visited[maxn];
int zk[4][2]={{1,0},{-1,0},{0,1},{0,-1}};//用于往上下左右扩展的数组
void GetL()//通过root数组得到LinJie数组
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(root[i][j])
{
for(int k=0;k<4;k++)
{
int z=root[i+zk[k][0]][j+zk[k][1]];
if(z)
LinJie[root[i][j]][z]=1;
}
}
}
}
}
int point(int u,int l)//匈牙利算法
{
for(int v=1;v<=l;v++)
{
if(LinJie[u][v]&&!visited[v])
{
visited[v]=1;
if(ny[v]==-1||point(ny[v],l))
{
nx[u]=v;
ny[v]=u;
return 1;
}
}
}
return 0;
}
int main()
{
cin>>t;
char op;
while (t--)
{
memset(root,0,sizeof(root));
cin>>n>>m;
int l=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>op;
if(op=='o')
root[i][j]=0; //没有城市,编号为0
else
root[i][j]=++l; //有城市,编号为l,我们给所有城市都定义一个编号
}
}
memset(LinJie,0,sizeof(LinJie));
GetL();//拆点得到我们需要的二分图
memset(nx,-1,sizeof(nx));
memset(ny,-1,sizeof(ny));
int res=0;
for(int i=1;i<=l;i++)
{
if(nx[i]==-1)
{
memset(visited,0,sizeof(visited));
res+=point(i,l);
}
}
cout<
例题三:【HDU1150】
题意:
有A,B两台机器,每个机器有一系列的工作模式,在某一次开启使用中只能处于其中的某一个模式,这个模式只有重启机器才能改变,一个工作i,(i,x,y)表示它可以在A机器的X模式,或者B机器的Y模式上工作,现在问至少要重启机器几次 才能够将所有的工作都做完。
思路:
二分图的模板题。我们以A机器的所有模式为左集合,以B机器的所有模式为右集合,以任务为边建立二分图,最后的结果就是该二分图的最小点覆盖集(选取最少的点,将图中所有的边都覆盖),我们通过定理:二分图的最大匹配数=二分图的最小点覆盖集,关于这个定理,我也不会证明,想看证明的同学,请看这篇博客:大佬的博客
代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
#define MAXN 110
typedef long long ll;
using namespace std;
int A,B,n;
int e[MAXN][MAXN];
int nx[MAXN],ny[MAXN];
int visited[MAXN];
int point(int u)//匈牙利算法
{
for(int v=1;v<=B;v++)
{
if(e[u][v]&&!visited[v])
{
visited[v]=1;
if(ny[v]==-1||point(ny[v]))
{
nx[u]=v;
ny[v]=u;
return 1;
}
}
}
return 0;
}
int main()
{
while (1)
{
memset(e,0,sizeof(e));
memset(nx,-1,sizeof(nx));
memset(ny,-1,sizeof(ny));
cin>>A>>B>>n;
if(A==0)
break ;
for(int i=0;i>j>>a>>b;
e[a][b]=1;
}
int ret=0;
for(int i=1;i<=B;i++)//基本的匈牙利算法
{
if(nx[i]==-1)
{
memset(visited,0,sizeof(visited));
ret+=point(i);
}
}
cout<
关于建图的一些注意事项:
在建图的时候一定要清楚图的点集和边集分别代表的含义。还有一点需要注意的是建图的时候要明确自己构建的二分图是有向图还是无向图,因为是否有向将会影响到最终二分图的匹配数。