学习算法和数据结构：字符串

说明：本来本篇应该作为「算法和数据结构」系列的“线性结构”部分（隶属关系），但是考虑到“串”作为数据结构的重要性，作此文以单独讨论“串”结构的相关特性；如无特殊说明，本文的“串”和“字符串”是一个意思

对了，本文最精彩的部分就是“KMP算法”理解部分(使用C语言、Java实现)

串的基本概念

串的定义：“串”是由零个或多个字符组成的有限序列，又名叫字符串
串的表示：一般记为 s = "a1a2...an" (n≥0) 其中s是串的名称，用双引号扩起来的字符是序列是串的值，注意引号不属于串的内容；ai（1≤i≤n）可以是字母、数字或其它字符，i就是该字符在串中的位置；串中的字符数目n称为串的长度，定义中谈到“有限”是指长度n是一个有限的数值；0个字符的串称空串，可以用""表示，也可以用希腊字母ø表示；所谓序列，说明相邻的字符间具有前趋和后继的关系

空串：长度为0的串
空格串：包含一个空格的串
子串和主串：子串在主串中的位置就是子串的第一个字符在主串中的序号

串的比较

字符串间的比较是通过组成字符串的字符之间的编码来进行的，而字符的编码指的是字符在对应字符集中的序号

计算机中的常用字符使用标准的ASCII编码：由7位二进制数表示一个字符，总共可以表示128个字符

给定的两个串s1= “a1a2…an”，t= “b1b2…bn”当满足下列条件之一时s
1. n
2. € k≤min(m,n), ai=bi(i=1,2...k-1)

串的抽象数据类型

串的逻辑类型和线性表很相似,不同之处在于串针对的是字符集,也就是串中的元素都是字符(重要!都是字符!)

串数据结构可以采取的操作有:
1. 查找元素;
2. 插入元素;
3. 删除元素;
4. 替换元素

串的存储结构

串的存储结构分为“顺序存储结构”和“链式存储结构”

串的顺序存储结构

“串的顺序存储结构”和“数组”相似

串的顺序存储结构用一组地址连续的存储单元来存储串中的字符序列,按照预定义的大小为每个串分配一个固定长度的存储区,一般用定长数组来定义
既然是定长数组,就存在一个预定义的最大串长度,一般可以将实际的串长度值保存在数组的0下标位置(当然也可以保存在最后一个元素中), 但是有的语言(比如C)觉得用一个数字占空间, 它规定在串值后面加一个不计入长度的结束标记字符, 比如\0来表示该串的终结; 这个时候, 可以使用遍历整个串以获取串的长度

对于串的顺序存储, 有一些变化, 串值的存储空间可以在程序执行过程中动态的分配而得; 在计算机中存在一个自由存储区, 叫“堆”, 可以由C语言的malloc()和free()函数来管理

串的链式存储结构

“串的链式存储结构”和“线性表”相似
考虑到串中的元素都是字符, 在实际操作中, 往往一个结点中会存储多个字符(类似“块链表”); 这样一来一个结点存放的字符个数就变得直观重要
串的来闹事存储结构除了连接串与串草操作时有一定的方便之外, 总的来说不如顺序存取灵活,性能也不如顺序存取好

朴素的模式匹配算法

概要：将串的每个元素作为循环查找的首元素，与要匹配的字符串进行配对
实现（S和T的长度存在主串S[0]与子串T[0]中）：

int Index(String S, String T, int pos)
{
    int i = pos;  /*i用于主串S中当前位置下标，如pos≠1则从pos开始匹配*/
    int j = 1;  /*j用于子串T中当前位置下标值*/
    while(i<=S[0] && j<=T[0]){
        if(s[i] == T[j]){
            ++i;
            ++j;
        }else{
            i = i-j+2;
            j = 1;  /*j退回到子串T的首位*/
        }
    }
    if(j > T[0]){
        return i-T[0];
    }else{
        return 0;
    }
}

再来一段Java实现（图示）：

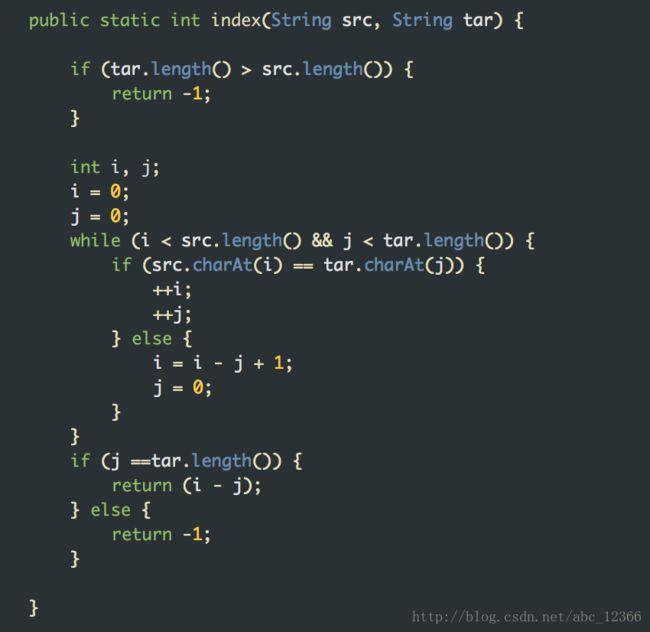
非常简单，唯一需要说明的就是每次主串下标i会退到i-j+2（Java，因为字符串元素的下标从0开始而且不要使用第一位存储长度，所以i会退到i-j+1t），可以从相对运动的角度看（假设平局速度相等且为单位1，i-j是相对速度差值，带上一头一尾就是加1，再往后加1开始新的匹配）；朴素匹配算法的时间复杂度O(m*n)

KMP算法

KMP算法还是比较经典的，O(m+n)蛮快的

//next数组
void get_next(String T, int *next)
{
    int i, j;
    i=1;
    j=0;
    next[1] = 0;
    while(i<T[0]){
        if(j==0 || T[i]==T[j]){
            ++i;
            ++j;
            next[i] = j;
        }else{
            j = next[j];
        }
    }
}

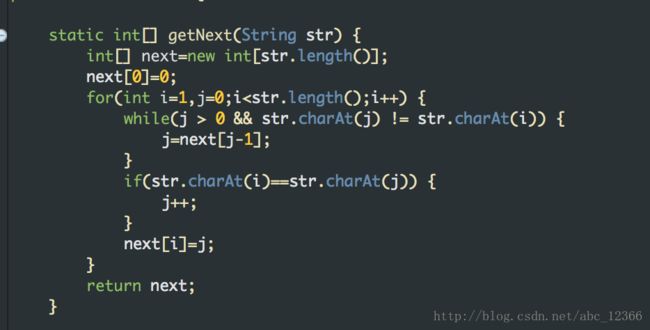
关于next数组的求法请移步：
从运动的角度看KMP的next数组

关于字符串的匹配，除了“朴素暴力求法”、“看毛片算法”外，还有“Horspool算法”、“Boyer-Moore算法”、“Sunday算法”、“RK算法”等等