二分图相关概念及匈牙利算法求解最大匹配（附代码实现）

“匈牙利算法”最早是由匈牙利数学家D.Koning用来求矩阵中0元素的个数的一种方法,由此他证明了“矩阵中独立0元素的最多个数等于能覆盖所有0元素的最少直线数”。1955年由W.W.Kuhn在求解著名的指派问题时引用了这一结论, 并对具体算法做了改进,仍然称为“匈牙利算法”。

图论中相关概念

二分图：

简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集U和V，使得每一条边都分别连接U、V中的顶点。如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图2的形式。

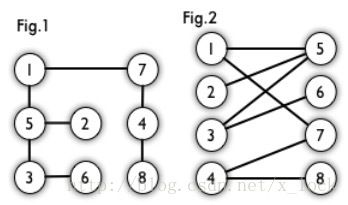
匹配：

在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配。

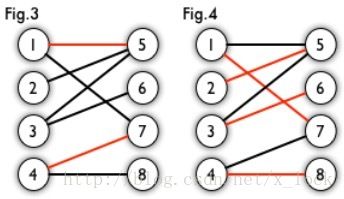
我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

最大匹配：

一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

完美匹配：

如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。

最大匹配数：最大匹配的匹配边的数目。

最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择。最小覆盖要求用最少的点（ＸＸ集合或ＹＹ集合的都行）让每条边都至少和其中一个点关联。可以证明：最少的点（即覆盖数）＝最大匹配数

最大独立数：选取最多的点，使任意所选两点均不相连。

最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径，路径长可以为 0（即单个点）。也就是说用尽量少的不相交简单路径覆盖DAG的所有结点。解决此类问题可以建立一个二分图模型。把所有顶点i拆成两个：ＸＸ结点集中的ii和YY结点集中的i′i′,如果有边i→ji→j，则在二分图中引入边i→j′i→j′，设二分图最大匹配为m,则结果就是n-m。

从上述概念描述中可以得到三个定理:
定理1：最大匹配数 = 最小点覆盖数（这是 Konig 定理）
定理2：最大匹配数 = 最大独立数
定理3：最小路径覆盖数 = 顶点数 - 最大匹配数

匈牙利算法相关概念

求解最大匹配问题的一个算法是匈牙利算法，下面讲的概念都为这个算法服务。

交替路：

从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。

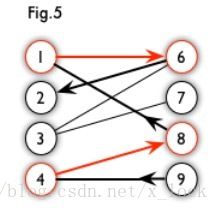
增广路：

从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出)

增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的,这也是算法的核心。在给出匈牙利算法 DFS 和 BFS 版本的代码之前，先讲一下匈牙利树。
匈牙利树一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 7，可以得到如图 8 的一棵BFS树：

这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点，那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示（顺便说一句，图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路，沿这条增广路扩充后将得到一个完美匹配）。

代码实现

class Max_match(object):
    def __init__(self, graph):
        self.g = graph
    def BFS_hungary(self):
        res=0
        Nx = len(self.g)
        Ny =  len(self.g[0])
        Mx = [-1]*Nx
        My = [-1]*Ny
        chk=[-1] * max(Nx,Ny)
        Q=[0 for i in range(Nx*Ny)]
        prev=[0] * max(Nx,Ny)
        for i in xrange(Nx):
            if Mx[i]==-1:
                qs=qe=0
                Q[qe]=i
                qe+=1
                prev[i]=-1
                flag=0
                while(qsand not flag):
                    u=Q[qs]
                    for v in xrange(Ny):
                        if flag:continue
                        if self.g[u][v] and chk[v]!=i:
                            chk[v]=i
                            Q[qe]=My[v]
                            qe+=1
                            if My[v]>=0:
                                prev[My[v]]=u
                            else:
                                flag=1
                                d,e=u,v
                                while d!=-1:
                                    t=Mx[d]
                                    Mx[d]=e
                                    My[e]=d
                                    d=prev[d]
                                    e=t
                    qs+=1
                if Mx[i]!=-1:
                    res+=1
        return res

本文主要参考了如下链接，尤其是第一个，但其代码实现有问题，此文用python重新实现：
【python实现的代码，封装的挺好，但有问题】
https://luzhijun.github.io/2016/10/10/%E5%8C%88%E7%89%99%E5%88%A9%E7%AE%97%E6%B3%95%E8%AF%A6%E8%A7%A3/
【讲的思路很清晰】
https://liam0205.me/2016/04/03/Hungarian-algorithm-in-the-maximum-matching-problem-of-bigraph/
【用python实现了,虽然封装的不友好，但可以用】
http://www.cnblogs.com/jamespei/p/5555734.html