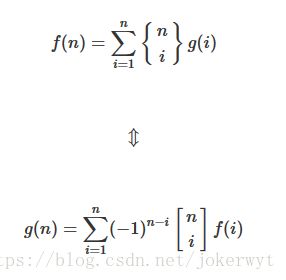jzoj4591 异或图（斯特林反演，线性基）

description

n<11,s<60

solution

这玩意儿让我想砸电脑怎么办

连通问题，发现不连通条件很简单，但连通条件很难处理。
即，枚举每个连通块内是哪些点（枚举子集划分）后，用线性基（或高斯消元求自由元？）可以较快地求出有多少种方案使得：不在同一子集中必定不连通，在同一子集中可能不连通。

所以容斥就好了，考虑一种确切的异或之后的图G，假如他有m个连通块，那么他会被包括

∑1≤i≤mS(m,i) ∑ 1 ≤ i ≤ m S ( m , i )

次。
（S是第二类斯特林数，含义是将m个连通块分进i个子集内）

按照容斥套路，考虑关于当前子集个数的容斥系数 g(i) g ( i ) ，我们需要构造一组f使得

∑1≤i≤mS(m,i)⋅g(i)=[m=1] ∑ 1 ≤ i ≤ m S ( m , i ) ⋅ g ( i ) = [ m = 1 ]

打表仔细找规律后 仔细推式子，根据斯特林反演，即

，令其中f(n)=[n=1]，可得出

g(x)=(−1)n−1(n−1)! g ( x ) = ( − 1 ) n − 1 ( n − 1 ) !

再来说说如何计算方案数，有子集划分之后，有一些位置是强制为0的。将这些位置提取出来做线性基，最后便是求异或和为0的方案数。（一开始直接做线性基，发现没法搞）假如线性基中插入了K个数，由于其中必定有异或和为0的方案（不妨考虑上选空集，对答案没有影响），我在未插入线性基的数中选出一个，再将其表示在线性基中的位置翻转（因为没被插入因此必定能表示），还是一种合法的异或和为0的方案。
因此，方案数是 2s−|B| 2 s − | B | ，乘上系数，统计进答案就行。

此题卡常，回消会T。

#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
int n,s,le,be[20],zero;
ll mi[100];
ll b[100],a[50],ans,base,jc[30];
char t[100];

void insert(ll x) {
    if (x==0) {
        zero=1;return;
    }
    for (int i = 45; ~i; i--) if (x & mi[i]) {
        if (a[i]) {
            x^=a[i];
            if (x == 0) {
                zero = 1;
                return;
            }
        } else {
            a[i]=x; base++;
            break;
        }
    }
}

void dfs(int x,int cnt) {
    if (x > n) {
        memset(a,0,sizeof a);
        ll z = 1, can = 0; ll ban = 0; zero = 0;

        for (int i = 1; i <= n; i++) for (int j = i+1; j <= n; j++) {
            if (be[i] != be[j]) ban+=z;
            z<<=1;
        }

        base=0;
        for (int i = 1; i <= s; i++) {
            insert(b[i] & ban); 
        }
        ans += jc[cnt-1] * (((cnt-1)&1) ? -1 : 1) * mi[s-base];
        return;
    }

    for (int i = 1; i <= cnt; i++) {
        be[x] = i;
        dfs(x+1,cnt);
    }

    be[x]=++cnt;
    dfs(x+1,cnt);
}

int main() {
    freopen("graph.in","r",stdin); 
    // freopen("graph.out","w",stdout);
    jc[0] = 1; for (int i = 1; i <= 10; i++) jc[i] = jc[i-1] * i;
    mi[0] = 1; for (int i = 1; i <= 60; i++) mi[i] = mi[i-1] * 2;
    cin>>s;
    for (int i = 1; i <= s; i++) {
        scanf("%s",t+1); le = strlen(t+1);
        for (int j = le; j; j--) b[i] = b[i] * 2 + t[j] - '0';
    }
    n = (sqrt(1 + 8 * le) + 1) / 2;
    dfs(1,0);
    cout<