【dicnic算法求最大流—匹配问题】座谈会的分配

这道题肝了好久。。。我感觉我一道题就没肝过这么久。。。气死了。。。。

思路：

就是用dicnic算法求最大流的问题，关键在于如何建图：

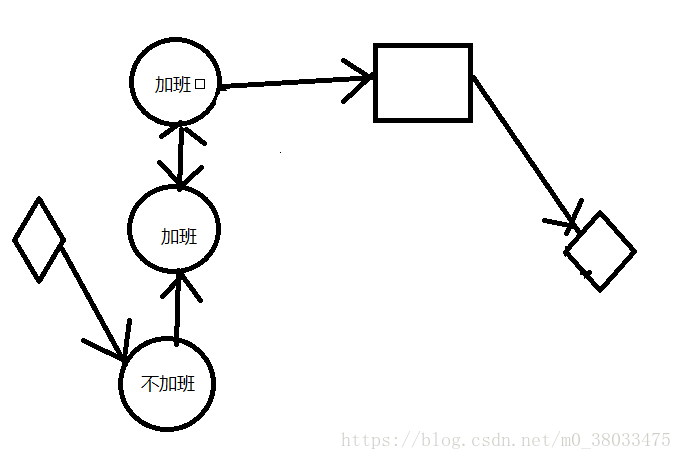
如图（图中边权值都为1），尤其是箭头的指向、源点和汇点的设计！

①箭头的指向：由员工指向外人，员工之间由不加班的指向加班的（这是为什么呢？我是用“抱过来”思想考虑的。因为你看看这个图嘛，其实是想把外人都“抱到”员工的座位上来，那么这样走过一条增广路就能解决一个外人的座位问题，对吧！那么因为加班的员工也可以去做身为他朋友的不加班员工的座位，那同理，是不是相当于不加班员工把加班员工“抱过来”坐着的意思呢？所以箭头就是“抱过来”的意思！），加班员工之间可以互相报所以设置双向边（即反相边权值为1），其他都设置单向边（即反向边权值为0）。

②源点出来指向的是不加班的人。这需要理解题意：加班的人有自己的位子要做，那些外人肯定是要坐不加班的人的位子。那么如果根据“抱过来”坐着的思想，肯定要先从一个空位子开始“抱过来”啊对吗？？！！

③所有外人指向汇点。这是显然的，因为我需要所有外人都找到位子，也就是都成功地被“抱到”空位子上，既然每个边流量都为1，看看最大流就知道最多能坐多少个外人了，只要最大流==外人数即可！

思路真的很难想我觉得，不过用“抱过来”思想一下就简单明了了。

代码：

#include
#include 
using namespace std;
const int maxn=1e3+5;
const int maxm=1e6;
struct edge
{
	int v,c,next;
}e[maxn];
int p[maxm];
int cnt=-1;
int isstaff[maxn];
int isinjob[maxn];
void init()
{
	memset(isstaff,0,sizeof(isstaff));
    memset(isinjob,0,sizeof(isinjob));
	memset(p,-1,sizeof(p));
	cnt=-1;
}
void insert1(int u,int v,int c)
{
	e[++cnt].v=v;
	e[cnt].c=c;
	e[cnt].next=p[u];
	p[u]=cnt;
}

int d[maxn];
int n; //一共有多少人 
bool bfs(int s)
{
    memset(d,0,sizeof(d));
	d[s]=1; 
	queue q;
	q.push(s);
	while(q.empty()==false)
	{
		int u=q.front();
		q.pop();
		for(int i=p[u];i!=-1;i=e[i].next)
		{	
			int v=e[i].v;
			if(e[i].c>0 && d[v]==0)
			{
				d[v]=d[u]+1;
				q.push(v);			
			}
		}		
	}
	return (d[n+1]!=0);
}
int dfs(int s,int flow) //flow表示在该增广路上，s点之前所更新出来的最大流量 
{
	if(s==n+1)
		return flow;
	int res=0;
	for(int i=p[s];i!=-1;i=e[i].next)
	{
		int v=e[i].v;
		if(d[v]==d[s]+1 && e[i].c>0)
		{
			int temp=dfs(v,min(flow,e[i].c));
			flow-=temp;
			res+=temp;
			e[i].c-=temp;
			e[i^1].c+=temp;
			if(flow==0)
				break;	
		}
	}
	if(res==0) d[s]=-1;
	return res;
}

int main()
{
	int T;
	cin>>T;
	while(T--)
	{
		init();
		scanf("%d",&n);
		int kaihui=0; //记录开会人数 
		for(int i=1;i<=n;i++)
		{
			scanf("%d",&isstaff[i]); //1表示是员工
			if(isstaff[i]==0)       //构图右边 
			{
				insert1(i,n+1,1); 
				insert1(n+1,i,0);
				kaihui++; 
			}
		}
		for(int i=1;i<=n;i++)
		{
			scanf("%d",&isinjob[i]); //0表示加班 
			if(isstaff[i]==1 && isinjob[i]==1) //构图左边
			{
				insert1(0,i,1); 
				insert1(i,0,0);
			} 
		}
		int relationship;
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				scanf("%d",&relationship);
				if(i>=j) continue;
				if(relationship==0) continue;

				if(isstaff[i]==1 && isinjob[i]==0)  //加班的人 
				{
					if(isstaff[j]==1 && isinjob[j]==0) //遇到加班的 
					{
						insert1(i,j,1);
						insert1(j,i,1); //这里不用连反向边了，本来就有了。 
					}
					else if(isstaff[j]==1 && isinjob[j]==1) //遇到不加班的 
					{
						insert1(j,i,1);
						insert1(i,j,0);
					}
					else if(isstaff[j]==0)  //遇到外人 
					{
						insert1(i,j,1);
						insert1(j,i,0);
					}
				}
				else if(isstaff[i]==1 && isinjob[i]==1) //不加班的人 
				{
					if(isstaff[j]==1 && isinjob[j]==0) //遇到加班的 
					{
						insert1(i,j,1);
						insert1(j,i,0);
					} 
					else if(isstaff[j]==0) //遇到外人 
					{
						insert1(i,j,1);
						insert1(j,i,0);
					}
				}
				else if(isstaff[i]==0)//外人 
				{
					if(isstaff[j]==1)
					{
						insert1(j,i,1);
						insert1(i,j,0); 
					}
				}
			}
		}
		int res=0;
		while(bfs(0))
		{
			res+=dfs(0,0x3f3f3f3f);
		}
		if(res!=kaihui) cout<<"T_T"<

我在手写代码中出现了一些“致命”问题，这里强调一下：

①对于这种多组数据，链式前向星的初始化不仅要初始化p数组，还要初始化cnt啊！！！md!!

②bfs更新层次每次都需要重新初始化记录层次的d数组。

③dfs中别忘了一开始就要写递归的临界条件。。。（无语）