图的拓扑排序

拓扑排序，很容易理解，在这里还是记录下，以后肯定会用到。

 

目录

小小事例

AOV网和AOE网

拓扑排序

---

 

小小事例

举个例子，假如某个工程由P1~P9共9个活动组成，这些活动的依赖关系如下表所示：

由上表可以得出以下结论：

 

 

---

AOV网和AOE网

图的主要元素是顶点和边，用有向无环图表示工程活动之间的关系时，根据顶点和边所代表的的意义不同，通常有两种常见的表示方法，分别为AOV网和AOE网。

AOV网：图中顶点代表的是活动，有向边代表的是与此边相连的两个活动的前后关系。

AOE网：图中边代表的是活动，边的权表示完成活动所需要的时间，与边相连的两个顶点分别表示活动的开始事件和结束事件。

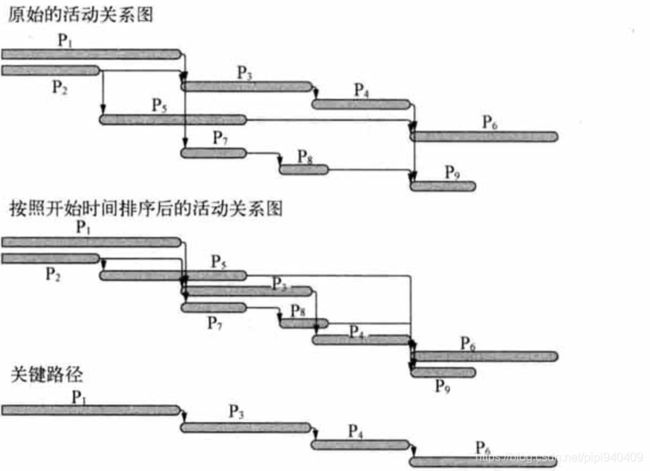
用AOV网表示上表如下图：

 

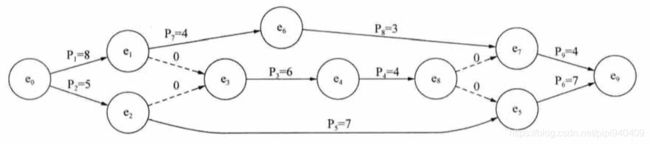
用AOE网表示上表如下图：

 

 

 

---

拓扑排序

拓扑序列：一个有向无环图的所有顶点可以排成一个线性序列，当这个线性序列满足以下条件时，该序列为一个满足图的拓扑次序的序列。

1、图中的每个顶点在序列中只出现一次。

2、对于图中的任意一条有向边(u,v)，在该序列中顶点u一定位于顶点v之前。

这样的序列被称为拓扑序列。

拓扑排序的基本过程：

(1)、从有向图中选择一个没有前驱（入度为0）的顶点，输出这个顶点；

(2)、从有向图中删除该顶点，同时删除由该顶点发出的所有有向边。

重复上述步骤（1）和（2），直到图中不再有入度为0的顶点为止。

判定结果，如果所有的顶点都已经输出，则顺序输出的顶点序列就是一个拓扑序列，如果图中还有未输出的顶点，但是入度都不为0，则说明有向图中存在环路，不能进行拓扑排序。

---

在工程实施中，人们总是希望每个活动尽早开始，所以在拓扑排序中，将活动的开始事件考虑进来。

每个活动的开始事件受前置活动的约束，但可以推算出来，具体推算方法如下：

1、如果一个活动没有前驱活动，则这个活动的开始时间是0；

2、如果一个活动有前驱活动，则这个活动的开始时间是前驱活动的开始时间和前驱活动持续时间的和，如果一个活动有多个前驱活动，则这个活动的开始时间是这些和中最大的一个。

每个活动的开始时间如上图AOV网所示。

---

 

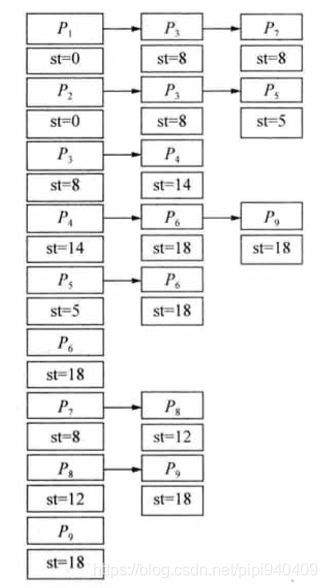
对于AOV网，用邻接表方式定义有向图的数据是最常用的方式，如下图：

图的数据结构描述如下：

typedef struct tagVertexNode
{
    char *name;    //活动名称
    int days;      //完成活动所需时间
    int sTime;     //活动最早开始时间
    int inCount;   //活动的前驱节点个数
    int adjacent;  //相邻活动的个数
    int adjacentNode[MAX_VERTEXNODE]; //相邻活动列表(节点索引)
}VERTEX_NODE;

图的定义如下：

typedef struct tagGraph
{
    int count;    //图的顶点个数
    VERTEX_NODE vertexs[MAX_VERTEXNODE]; //图的顶点列表
}GRAPH;

由于考虑到开始时间的问题，即开始时间越早的活动越早开始，所以使用优先级队列即可完美的解决此问题。

拓扑排序的核心算法如下：

bool TopologicalSorting(GRAPH *g,std::vector& sortedNode)
{
    std:::priority_queue nodeQueue;
    for(int i=0;icount;i++)
    {
        if(g->vertexs[i].inCount == 0)
        {
            EnQueue(nodeQueue,i,g->vertexs[i].sTime);
        }
    }
    while(nodeQueue.size()!=0)
    {
        int node = DeQueue(nodeQueue);    //按照开始时间优先级出队
        sorteNode.push_back(node);        //输出当前节点
        //遍历节点node的所有邻接点，将表示有向边的inCount值减1
        for(int j=0;jvertexs[node].adjacent;j++)
        {
            int adjNode = g->vertexs[node].adjacentNode[j];
            g->vertexs[adjNode].inCount--;
            //如果inCount值为0，则该节点入队
            if(g->vertexs[adjNode].inCount ==0)
            {
                EnQueue(nodeQueue,adjNode,g->vertexs[adjNode].sTime);
            }    
        }
    }
    return (sorteNode.size() == g->count);
}

算法结束后，判断输出的排序列表sorteNode，如果sorteNode中的节点个数与图的顶点个数相同，则说明所有顶点都已经输出，拓扑排序完成，否则就说明图中存在环路，无法进行拓扑排序。