Python学习之基础学习3
经过前两天的学习,我们已经基本能编写一些小型的Python程序,今天自己找了一些有趣的例子来练练手,例子来源为https://github.com/jackfrued/Python-100-Days和牛客网。
1、寻找水仙花数
水仙花数(Narcissistic number)也被称为超完全数字不变数(pluperfect digital invariant, PPDI)、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数(Armstrong number),水仙花数是指一个 3 位数,它的每个位上的数字的 3次幂之和等于它本身(例如:1^3 + 5^3+ 3^3 = 153)。
下面给出相应的程序:
#寻找水仙花数
import numpy as np
shuixianhuanumber = []
for i in range(100,1000):
gewei = np.mod(i,10)
shiwei = np.mod(i//10,10)
baiwei = i//100
if gewei**3+shiwei**3+baiwei**3-i == 0:
shuixianhuanumber.append(i)
print('水仙花数有:',shuixianhuanumber)2、寻找完美数
完全数(Perfect number),又称完美数或完备数,是一些特殊的自然数。它所有的真因子(即除了自身以外的约数)的和(即因子函数),恰好等于它本身。如果一个数恰好等于它的因子之和,则称该数为“完全数”。第一个完全数是6,第二个完全数是28,第三个完全数是496,后面的完全数还有8128、33550336等等。
下面给出相应的程序:
#寻找完全数
import numpy as np
wanmeishu = []
for i in range(1,1000):
#寻找约数
yueshu = []
for j in range(1,i):
if np.mod(i,j) == 0:
yueshu.append(j)
if sum(yueshu)-i == 0:
wanmeishu.append(i)
print('1000以内的完美数有:',wanmeishu)3、百鸡百钱问题
我国古代数学家张丘建在《算经》一书中提出的数学问题:鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。百钱买百鸡,问鸡翁、鸡母、鸡雏各几何?其实这个问题就是求解一个带约束的方程问题。
下面给出相应的程序:
#求解百钱百鸡问题
for num_cock in range(0,100):
for num_hen in range(0,100):
if 14*num_cock + 8*num_hen -200 == 0 and 100-num_hen-num_cock >= 0:
print('公鸡{0}只,母鸡{1}只,雏鸡{2}只'.format(num_cock,num_hen,(100-num_cock-num_hen)))4.生成斐波那切数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用。
下面给出相应的程序:
#生成斐波那契数列
def BuiltFibonacci(len):
F_1 = 1
F_2 = 1
Fi = [1,1]
count = 1;
while(count < len):
F_next = F_1 + F_2
Fi.append(F_next)
F_1 = F_2
F_2 = F_next
count += 1
return Fi
F_out = BuiltFibonacci(20)5、Craps赌博游戏
Craps游戏的游戏规则十分简单:玩家掷两个骰子,点数为1到6,如果第一次点数和为7或11,则玩家胜,如果点数和为2、3或12,则玩家输,如果和为其他点数,则记录第一次点数和,然后继续掷骰子,直至点数和等于第一次掷出的点数和,则玩家胜,如果在这之前掷出了点数和为7,则玩家输。
下面给出相应的程序:
#Craps赌博游戏
import numpy as np
your_money = 1000
while(your_money > 0):
money_bet = int(input('你现在的资产为{0},请选择下注金额:'.format(your_money)))
seed1 = np.random.randint(1,7)
seed2 = np.random.randint(1,7)
seed_sum = seed1+seed2
if seed1+seed2 == 7 or seed1+seed2 == 11:
your_money = your_money + money_bet
print('玩家胜')
elif seed1+seed2 ==2 or seed1+seed2 == 3 or seed1+seed2 == 12 :
your_money = your_money - money_bet
print('玩家输')
if your_money <= 0:
print('你的钱已经输完,你已经出局!')
break
else:
print('平局,继续摇色子')
seed1 = np.random.randint(1,7)
seed2 = np.random.randint(1,7)
seed_sum_new = seed1+seed2
while(1):
if seed_sum_new == seed_sum:
print('玩家胜')
your_money = your_money + money_bet
break
elif seed_sum_new == 7:
print('玩家输')
your_money = your_money - money_bet
break
else:
print('又平局了,继续要摇色子')
seed1 = np.random.randint(1,7)
seed2 = np.random.randint(1,7)
seed_sum_new = seed1+seed2
print('你的钱已经输完了,出局了')6、计数器问题
题目描述:
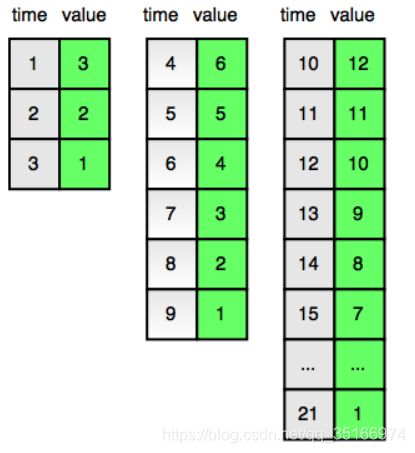
小爱有一个奇怪的计数器。在第一个时刻计数器显示数字3,在接下来的每一个时刻,屏幕上的数字都会减1,直到减到1为止。
接下来,计数器会重置为上一个计数周期初始值的两倍,然后再每一个时刻减1。具体过程如下图所示:
找出规律,并打印出t时刻计数器的值。
下面给出相应的程序:
Number = int(input())
n = 1
while 3*((2**n)-1) < Number:
n = n+1
Max_number_series = 3*((2**n)-1)-3*((2**(n-1))-1)
First_true_number = 3*((2**(n-1))-1)+1
Subtract_number = Number - First_true_number
True_number = Max_number_series - Subtract_number
print(True_number)7、非整除集合问题
题目描述:
给定一个由正整数组成的集合S,找出一个最大的子集合S·,使得S·中任意两个数字的和都不能被K整除,求出S-长度的最大值。例如S=「10,10,12,19,22,24,25」,K=4。S·的可能取值为「10,12,25」或者「19,22,25」等,S·最多只能取3个数。
下面给出相应的程序:
import numpy as np
S_and_K = input('Please input the length of S and K:')
S = input('Please input S:')
S_and_K_real = np.array(S_and_K.split(' '),dtype = np.int);
S_length = S_and_K_real[0]
K = S_and_K_real[1]
S_real = np.array(S.split(' '),dtype = np.int)
tmp = np.ones([S_length,1],dtype = np.int)
matrix1 = tmp*S_real
matrix2 = matrix1.T
matrix_final = matrix1 + matrix2
matrix_mod = np.mod(matrix_final,K)
max_length = 1
for i in range(S_length):
matrix_mod_lines = matrix_mod[i,:]
tmp_length = S_length-len(np.flatnonzero(matrix_mod_lines))
if tmp_length > max_length:
max_length = tmp_length
print('The longest length of S- is:',max_length)