搜索2——广搜深搜
总共带了两双鞋都湿了,现在都开始穿拖鞋上课了。宿舍楼旁边那个湖,一直以为是人工湖,最近才发现原来是下水道。现在想想我当时为什么不报河南工程。。。烦气。都是老杨在那个牌上,把河南工程放下面了,再次诅咒老杨,蹲厕所没有手纸。
广度优先搜索和深度优先搜索主要是用于图的遍历。今天先不说图先把搜索总结完。
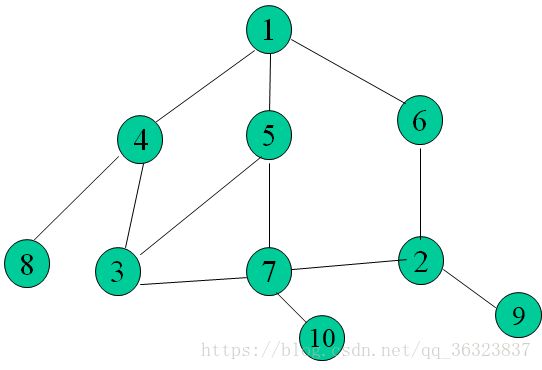
广度搜索:按层次来遍历。通常是用队列来写的。从某点出发(入队)判断当前点是否符合条件决定是否返回出队当前点,并入队与当前点连接的点,再出队该点最后前进至下一个点。例如
当前在点4入队并出队了点1,我们首先判断点4是否符合条件再a[++head]=x入队8和3。再出队点4然后前进一位到点5判断点5是否符合条件。直到这一层都遍历了一遍到点8。然后就。。。整体顺序是1 4 5 6 8 3 7 2 10 9
代码如下:
Void bfs(int i);
{
int head=0,tail=1,j;
memset(q,0,sizeof(q));
q[1]=i; f[i]=1;
while (head使用广度优先搜索法时,离根节点最近的节点先扩展,所以广度优先搜索法比较适合求步数最少解的问题。
深度优先搜索:通常是用递归来写,从当前点出发 选择一个未被访问的邻接点,不断重复着一个过程,知道这个分支被访问完,再重新返回父节点,从另一个邻接点再继续进行深搜。这里还用刚才那个例子:
假如现在在点5,判断当前点是否符合条件,决定是否返回。若点7未被访问过,就前进至第点7。直到这一这一分支访问完。返回点至5访问点三当然前提是点3未访问过。顺序是1 4 8 3 5 7 10 2 9 6
代码如下
Void dfs(int k)
{
printf(“%d”,k);
f[k]=1;
for (int j=1;j<=n;j++)
if (f[j]!=1&& a[k][j]==1) dfs(j);
}
搜索的优化通常是以分支的选择顺序(搜索序的选择),减少分支的思路来考虑的.下面是一位大牛对三个例子的分析:
问题1《Line》
【问题简述】
给出一个数N(N<=76)。然后将1至N这N个数每个数字使用两次来构造序列,使序列中数字为i的两项中间恰好有i个数,求满足该条件的序列。
【分析】
首先我们确定搜索对象为数字,每个数字搜索的状态空间为数组的第1位至第2N位,那么搜索序该如何选择呢?
考查搜索树的形态:
(1)数字从小到大: 第一层的数字1有2n-2种选择,层数越大的数字选择越少。
(2)数字从大到小: 第一层的数字n有n-1种选择,层数越大的数字选择越多。
相比较,(1)的搜索树形态上宽下窄,(2)的搜索树形态上窄下宽。
直觉告诉我们:第二种搜索序能够更快得到解。而程序运行结果也证明:对于较大n,从大到小搜索效率高得多。
问题1告诉我们:取值范围小的搜索元素先搜索,可以更快得到一组可行解。
问题2《cake》(noi99)
【问题简述】
做一个由m个圆柱组成的生日蛋糕,要求所有上层的圆柱的高度小于下层,半径也小于下层,且高度和半径都是整数,体积必须是严格的n*π,求最小表面积(不算底面),输出表面积除以π的值。
【分析】
此题即要求两个长度为m的递增整数数列r和h,且满足
,
要求使 最小。
显然,搜索对象为每层蛋糕,那么,搜索顺序该如何选择呢?设:蛋糕的顶层看作第1层,底层看作第m层。从下往上搜相对于从上往下搜有两大优势:
(1)先确定了最低层的h和r,为之后的h和r的枚举提供一个上界。
(2)注意到表面积包括每层蛋糕的侧面积和裸露的顶面积。确定了最底层的蛋糕就确定
了每层蛋糕裸露的顶面积之和,需要考虑的只剩下每层蛋糕的侧面积。
搜索序确定后,还要考虑剪枝:
(1)可行性剪枝(h,r为整数):当前剩余的体积left不够塔建i层的最小体积。
(2)最优化剪枝:当前求出的s+剩余最小侧面积>ans。
当然,本题最强的条件是体积限制,即根据问题性质,利用数学公式变形,使剩余体积left影响最优性剪枝条件,此处不予讨论。
问题3《sudoku》(noip2009)
【问题简述】
一个靶形数独,规格为9 格宽×9 格高的大九宫格中有 9 个 3 格宽×3
格高的小九宫格,在这个大九宫格中,有一些数字是已知的,根据这些数字,利用逻辑推理,在其他的空格上填入 1到
9 的数字。要求:每个数字在每个小九宫格内不能重复出现,每个数字在每行、每列也不能重复出现。每一个方格都有一个分值,离中心越近则分值越高。靶形数独的得分为填满数字后,每个格子的数字与这个格子的分值的乘积之和,求给定靶形数独的最高得分。
【分析】
此题最朴素的想法自然是对于每一个未填入数字的方格,枚举填入该方格的数字是多少,然后向后继续尝试,在所有可行解中记录最优解,最后输出即可。那么,该如何确定搜索序和剪枝呢?
一般来说,可以采用两种搜索序:
(1)按照从上到下,从左到右的顺序搜索。
(2)从中心开始,一圈一圈呈螺旋状向外搜索。
第二种搜索序基于一种贪心思想(因为越靠近中心,点的权值越高,让靠近中心的点的数字越大,得分也就可能越高),目的在于更快地确定一个较优或最优的解来方便以后的最优性剪枝。
咋一看,可能会觉得第二种似乎会好,但事实证明,第一种才是更好的那一种(第一种得75分;第二种得35分)!这是为什么呢?
分析两种搜索序中每一个点确定后对以后的影响。
第一种:确定一个点后,下一个点一定可以被这个点上方的所有点和左方的所有点限制到,而同一九宫格的点也同时被尽可能地确定了。一定程度上,下一个点的取值受到较大的限制。
第二种:确定一个点后,下一个点的上下左右不一定已经被确定,虽然同一九宫格的点也被尽可能地确定,但是很明显,它在开始搜索时提供的限制太少了。
可以发现,第二种搜索序造成了搜索树在前面几层宽度较大,所以走到的无用状态也多了,从而影响了整体效率。
【进一步分析】
由问题1可知:取值范围小的元素先搜索,可以使搜索树的形态较瘦,提高搜索效率。
对于本题,在某一格局下,每个未填格子可填的数字个数可以求出,每次让当前可填数最少的格子先填数,搜索效率就会得到大幅提高。
最优性剪枝:当发现剩下的格子无论填多大时都比当前最优值小,就剪枝。
问题3告诉我们:取值范围小的搜索元素先搜索可以使搜索树更窄,使剪枝更加有效。
从上面的讨论中可以看出,选择合理的搜索顺序对某一类搜索算法的效率起着重要作用,这样的例子还有很多,:比如算符破译(NOI2000),质数方阵(IOI94),篮球锦标赛(BOI98)等。但搜索顺序的选择仅依靠一些基本的方法和思想是不够的,它需要对问题进行全面、透彻的分析,深入挖掘问题的本质,找出优化算法的突破口。