词法分析——DFA 的最小化:Hopcroft 算法
通过前面对于词法自动生成部分的学习,我们已经掌握了如何从源码生成到 DFA
那么为什么要对 DFA 进行最小化处理呢?
下面给出一个例子:
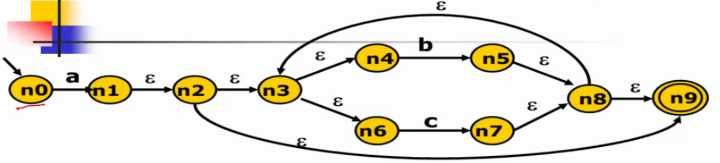
如下是我们之前写出的 a(b|c)* 的 NFA:
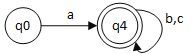
它可以对应转换成如下的 DFA:

在上面的 DFA 中非接受状态和接受状态是不能够合并的,因为如果合并,就会接受一个 ϵ \epsilon ϵ串,这是明显不正确的。但是如果同样是接受状态或者同样是非接受状态的话就有可能。例如可以将 q 2 q_2 q2和 q 3 q_3 q3进行合并,得到一个新的接受状态 q 4 q_4 q4。得到新的 DFA,如下:

之后,我们还可以再对 q 1 q_1 q1和 q 5 q_5 q5进行融合得到 q 5 q_5 q5。

这就是最终的状态最少的 DFA。
最小化得到状态最少的 DFA 的好处在于,因为 DFA 最后的代码实现是在作为内部的一个数据结构表示,如果状态和边越少,则它占用的计算资源(内存、cache)会更少 ,可以提高算法的运行效率和速度。
Hopcroft 算法
//基于等价类的思想
split(S)
foreach(character c)
if(c can split s)
split s into T1, ..., Tk
hopcroft()
split all nodes into N, A
while(set is still changes)
split(s)

q 1 , q 2 , q 3 q_1,q_2,q_3 q1,q2,q3都有对状态 a 的转移,但是 q 1 q_1 q1和 q 2 q_2 q2转移到了同样的一个状态 S2, q 3 q_3 q3 转移到了 S3。所以 q 1 q_1 q1, q 2 q_2 q2可以看做一组,因为它们对 a 的行为是一致的,都到了 S2。 q 3 q_3 q3单独一组。所以 a 这个字符将 S1 切为了两个子集。这就是等价类的思想。
Hopsroft 算法就是先根据非终结状态与非终结状态将所有的节点分为 N 和 A 两大类。 N 为非终结状态,A 为终结状态,之后再对每一组运用基于等价类实现的切割算法。
举个例子

对于之前给出的 DFA 的例子,我们首先将其切分为 N 和 A, N 是 q 0 q_0 q0, A 是 { q 1 q_1 q1, q 2 q_2 q2, q 3 q_3 q3}。
在 A 中,字符b,c的状态转移,每个节点最后得到的都还是 A 这个状态,无法对 q 1 , q 2 , q 3 q_1,q_2,q_3 q1,q2,q3进行区分。所以就将这三个节点融合为一个新的节点 q 4 q_4 q4。
再给一个例子

N : { q 0 , q 1 , q 2 , q 4 q_0,q_1,q_2,q_4 q0,q1,q2,q4}
A : { q 3 , q 5 q_3,q_5 q3,q5}
在 N 中 q 0 q_0 q0和 q 1 q_1 q1在接受 e 的条件下最终得到的状态还是在 N 的内部,但是 q 3 q_3 q3和 q 4 q_4 q4接受e的条件下得到的状态是A。所以可以将其根据 e 拆分成 { q 0 , q 1 q_0,q_1 q0,q1},{ q 2 , q 4 q_2,q_4 q2,q4},{ q 3 , q 5 q_3, q_5 q3,q5}
对于 q 2 q_2 q2和 q 4 q_4 q4都可以接受e,而且最终达到的状态一致,所以不能再进行切分。
q 0 q_0 q0和 q 1 q_1 q1,在接受 e 的时候, q 0 q_0 q0最终得到还是在 { q 0 , q 1 q_0, q_1 q0,q1}这个状态的结合中, q 1 q_1 q1却会落在{ q 2 , q 4 q_2,q_4 q2,q4} 的状态中,所以可以将 q 0 q_0 q0和 q 1 q_1 q1分为{ q 0 q_0 q0},{ q 1 q_1 q1}。
