求和最大的子段

题目：

给你一串数字，可正，可负，可零。让你找到其中累计和最大的子段的和，并且返回这个和。

思路：

我们给出四中解决方案，这四种解决方案的时间复杂度从高到低。

方案一：

枚举所有的数组所有的区间，求出累加和，比较大小，最后得出结果。

时间复杂度为O(n^3).

代码：

#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
#define MAXN 10000
typedef long long ll;
using namespace std;
int arr[MAXN];
int n;
int GetMax()
{
    int MainSum=INT_MIN;
    for(int i=1;iMainSum)//找到了一个和更大的子区间
                MainSum=sum;
        }
    }
    return MainSum;

}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>arr[i];
    cout<

方案二：

还是枚举所有区间，但是在求区间累加和时我们运用上一次求的结果来进行递推。

时间复杂度为O(n^2)

代码：

#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
#define MAXN 10000
typedef long long ll;
using namespace std;
int arr[MAXN];
int n;
int GetMax()
{
    int MainSum=INT_MIN;
    for(int i=1;iMainSum)
                MainSum=sum;
        }
    }
    return MainSum;

}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>arr[i];
    cout<

思路三：

分而治之的思想，每次将数组从中间分开，递归求解左边子区间的最大累加和和右边子区间的最大累加和，然后求解跨中间位置的子区间的最大累加和，取这三种情况中累加和最大的返回给上一级。

时间复杂度为O(n*log(n))，O(n)是在递归函数中进行的操作的时间复杂度，O(log(n))是递归函数调用的时间复杂度(相当于调用log(n)次递归函数)。

代码：

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
#define MAXN 10000
typedef long long ll;
using namespace std;
int arr[MAXN];
int n;
int GetMax(int l,int r)//二分思想
{
    if(l==r)
        return arr[l];
    int mid=(l+r)/2;
    int Right=GetMax(l,mid);//得出mid位置右边的和最大的子区间的和
    int Left=GetMax(mid+1,r);//得出mid位置左边和最大的子区间的和
    int Middle=0;//保存跨mid位置的和最大的子区间的和
    int RightSum=0;
    int LeftSum=0;
    int rightsum=0;
    int leftsum=0;
    for(int i=mid+1;i<=r;i++)//从mid+1位置往后推，找出以mid+1位置为开头的和最大的子区间的和
    {
        rightsum+=arr[i];
        if(rightsum>RightSum)
            RightSum=rightsum;
    }
    for(int j=mid;j>=1;j--)//从mid位置往前推，找出以mid位置为结尾的和最大的子区间的和
    {
        leftsum+=arr[j];
        if(leftsum>LeftSum)
            LeftSum=leftsum;
    }
    Middle=RightSum+LeftSum;//得到跨mid位置的和最大的子区间的的
    return max(max(Right,Left),Middle);//返回最大那个
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>arr[i];
    cout<

思路四：

运用简而治之的思想，我们从后往前依次求所有的累加和，累加和一旦小于零，我们就可以在这串数字串中切除已经遍历过的位置，然后从剩下的数字串中继续进行上述操作。我们在运算中要保存最大的累加和。

分析可得，该算法的时间复杂度是O(n)，线性的，因为我们只要从后往前遍历一遍数组就可以得到结果了。

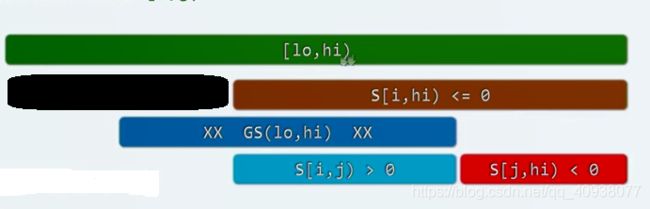
如果不懂思路的话，请看下面这张图：

下面来证明当累加和小于零时为啥可以直接切除数字串中的已经遍历过的那一部分：

我们只需要证明在上图中以黑色区域的某个位置为开头的最大累加和区间不会和棕色区域有任何瓜葛就行了，运用反证法，假设有瓜葛，那么就是图中深蓝色区域所示的状态。

如果棕色区域的累加和小于零的话，那么棕色区域的任意一段后缀子区域的累加和肯定大于零(如果存在累加和小于零的后缀子区域，那么就会在之前给切除了，就不会轮到现在切除棕色的区域了)。

假设上图中深蓝色的区域真实存在，那么必会有浅蓝色区域的累加和大于零(如果浅蓝色区域的累加和小于零，那么就不会选择浅蓝色区域了，因为浅蓝色区域只会让累加和变得更小)，深红色区域的累加和小于零(如果深红色区域大于零，那么就不会只选择浅蓝色区域了，也要把深红色区域也给选择上，因为深红色区域会让累加和变得更大)，至此，就出现了矛盾了----在棕色区域中存在一个后缀子区域的累加和小于零。

证毕。

代码：

#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
#define MAXN 10000
typedef long long ll;
using namespace std;
int arr[MAXN];
int n;
int GetMax()
{
    int End=n;
    int sum=0;
    int MainSum=0;
    for(int i=n;i>=1;i--)//从后往前遍历数组，得到累加和，只要是累计和小于零，就可以将已经遍历过的数组的这段区间给切除
    {
        sum+=arr[i];
        if(sum<0)
        {
            sum=0;
            End=i-1;
        }
        MainSum=sum;
    }
    return MainSum;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>arr[i];
    cout<