线性一致性理论

Jepsen(项目主页)是开源的分布式测试框架，基于Clojure语言，支持各种错误注入。目前广泛应用在各种分布式系统的测试中，尤其是一致性协议实现的测试中。Jepsen测试中支持验证系统的线性一致性，关于线性一致性，中文的介绍非常少，目前网上能搜到的大概只有tidb(一个创业公司PingCAP研发的分布式数据库)的一篇Linearizability 一致性验证。

要理解理论，最好的方法还是直接去看建立这个理论的原始论文，于是在业余时间对相关论文进行了阅读。其中第1)篇我做了一个完整的翻译，其他几篇由于篇幅和时间的原因仅进行了阅读。本文下面的内容主要源自阅读如下4篇论文后的理解，如果你觉得还有不好理解的地方欢迎指出，想深入了解一下的也可以再看下原文。首先简单介绍下每篇论文涉及的内容：

1) How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Programs Lamport 1979

    此文提供了关于Sequential Consistency一个简单精确的定义。不过它主要讲述的内容是关于：处理器和内存模块在什么条件下可以保证多处理器并行执行情况下的顺序一致性。这篇文章是Lamport在1979年发表的，距今已经40年，是cache-coherence领域最常被引用的一篇早期论文。它一直在我的reading list上，又非常简短(不到两页)，于是趁此机会就将它翻译了一遍：译文。为了理解Jepsen测试的原理，我们只需要理解这篇文章定义的Sequential Consistency概念即可。

2) Linearizability: A Correctness Condition for Concurrent Objects Maurice Herlihy · Jeannette M Wing 1990

    此文首次提出了Linearizability的概念。主要内容包含线性一致性模型的形式化定义，该模型的两个关键属性(locality和nonblocking)及其证明，还包含与其他一些模型比如Sequential Consistency/Serializability(可串行化)的对比。

3) Testing for Linearizability

    此文主要提出了用于可线性化验证的WGL算法，该算法是对WG算法的一个优化，并且包含了WG算法的相关内容。

4）Faster linearizability checking via P-compositionality*

    此文通过将线性一致性的locality属性(一个并发系统是可线性化的当且仅当它里面的所有对象都满足可线性化)背后的思想进行扩展，提出了P-compositionality*，然后基于这个概念可以实现更高效的线性化验证。核心的思想是将需要进行线性化验证的History(历史Operation序列)根据某种Partition方式划分成多个更小的子History，直接验证这些子History是否是可线性化的。

1 .顺序一致性(Sequential Consistency) vs 线性一致性(Linearizability)

论文1)中关于顺序一致性的原始定义如下：

"在设计和证明运行在该计算机上的多进程算法[1]-[3]的正确性时，通常基于如下假设：执行结果与这些处理器以某一串行顺序执行的结果相同，同时每个处理器内部操作的执行看起来又与程序描述的顺序一致。满足该条件的多处理器系统我们就认为是sequential consistent的"。这里的处理器就代表了一个独立的执行进程(或线程)，每个进程(线程)内部是串行执行的。如果并行执行的结果与某个合法的串行执行顺序(在这个执行顺序中每个线程内部的执行顺序要保留)的执行结果一致，我们就认为它是符合顺序一致性的。

我们以一个具体实例来说明顺序一致性与线性一致性的区别。假设我们目前有一个内存寄存器(Register)，该寄存器支持Set和Get操作。

现在两个线程P1 P2，它们会操作这一个寄存器，横轴代表时间，线程内部是串行执行，线程之间是并行的，假设现在观察到如下的一个执行历史。

该执行历史满足顺序一致，但违反了线性一致。

 

 具体原因解释如下：

对于顺序一致性来说，它要找到一个合法的顺序执行过程(只要能找到一个即可)，该执行过程要保留线程内部原有的顺序(对应到上图就是:[Set 1]一定要在[Get 2]之前，[Set 3]一定要在[Set 2]之前)。根据这个要求我们可以发现：[Set 1] [Set3] [Set 2] [Get 2]就是一个合法的顺序执行过程。对于一个寄存器来说，合法的顺序执行过程需要满足这个条件：Get到的值一定是最近一次Set的那个值。

而对于线性一致性来说，它也是要找到一个合法的顺序执行过程(只要能找到一个即可)。但是这个顺序执行过程，不仅要保留线程内部的先后顺序，还要保留线程之间的操作的先后顺序。比如上图从时间线上看，[Set 1]是最先发生的，[Get 2]和[Set 3]时间上有交叉，在线性一致性模型中，我们认为这两个是并行的，先后顺序不定，最后的[Set 2]一定是最后发生。这样满足线程内部和线程间顺序约束的执行过程只有两种，如上图所示。但是这两种执行过程都不是合法的：对于[Set 1] [Set 3] [Get2] [Set 2]来说，Set 3之后却Get到了2；对于[Set 1] [Get 2] [Set3] [Set 2]来说，Set 1之后却Get到了2。所以不满足线性一致性。

通过这个例子我们得到了一个关于线性一致性的直观认识：它比顺序一致性具有更强的约束，一个合法的顺序执行过程除了要保留线程内部的执行顺序外，还要保留线程间操作的先后顺序。一个系统满足线性一致性，那么它一定满足顺序一致性，反过来不成立。

2 线性一致性理论模型

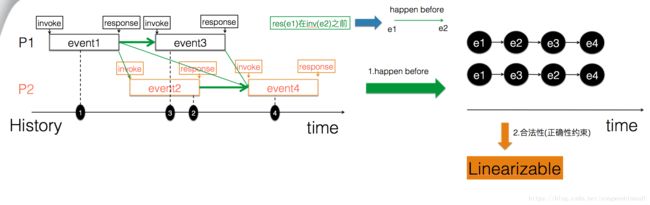
现在看一下，怎么用线性一致性的理论模型来描述上面的例子，具体如下图所示。

首先在线性一致性模型中，把某个操作抽象为一个事件(对应到实际系统中，可以是一个多线程程序中的本地函数调用，也可以是分布式系统中的一个rpc call)。每个事件起始于invoke发出，终止于收到response。同时定义事件间的如下happen before关系：

对于事件e1和e2来说，如果事件e1的response是在事件e2的invoke之前，我们就说e1 happen before e2。

对于同一个线程来说，前面的事件一定happen before后面的事件。但是对于不同线程上的两个事件来说，它们之间只有在在时间线上没有交叉的情况下，才会存在happen before关系。对于有交叉的那些事件，比如下图中的event2和event3，它们两个就不存在happen before关系，对于我们要寻找的合法顺序执行过程来说，它们两个的顺序可以是任意的。如下图，事件间的所有happen before关系用绿线表示。

 History：是由事件组成的一个执行历史，如上图就是一个执行历史。如果对于一个History来说，我们可以找到一个顺序执行过程，该顺序执行过程满足如下条件：

1.保留了History中所有事件的happen before关系 2.是一个合法的顺序执行过程

我们就说这个History(历史执行过程)是可线性化的。

如果一个系统的所有执行过程都是可线性化的，那么我们就说该系统是线性一致的。

3 可线性化验证算法

给定一个History，怎么判断它是不是可线性化的呢？最简单的方法就是枚举，我们把给定History中包含的事件进行全排列，排除掉违反了happen before约束的那些排列方式，然后对剩余的进行验证，如果能找到一个合法的执行过程，我们就认为它这个History是可线性化的。但是这个算法的复杂度是n!，如果History包含了比较多的事件，基本上就没法接受了。

下面的算法针对这一问题提出了不同的优化思路。

3.1 WG算法

具体的算法伪代码如下：

这个算法是递归的，就是对于给定History，不断从里面找合法的minimal operation的过程。

关于minimal operation的定义如下：

minimal op：no op happen before it.

从时间线上看，在最左侧的那个事件以及与它有交集的事件，都属于minimal operation。

这个算法是在保证满足happen before的前提下进行搜索，排除掉那些不满足happen before关系的搜索路径。如果当前操作作用到对象后还是合法的，就继续递归往下走，看剩余的操作能否找到一个合法的顺序执行过程，如果剩余的能直接找到就返回成功。如果当前操作不合法，就把对象恢复到当前操作之前的状态，然后尝试下一个minimal op，继续搜索。

这个算法比简单全排列要快，比如History中的事件之间很多都具有happen before关系，搜索会很快。但是如果有很多并行的事件，比如下图所示的极端情况下所有事件都是并行的，那么复杂度也会退化到n!。

 

3.2  WGL算法

WGL算法是对WG算法的优化。它主要基于如下观察：

1.执行过程中的相邻的两个读操作可以交换顺序 R1 R2 = R2 R1，因为相邻改变顺序后，读取的内容不变，同时对象的状态也不会改变

2.状态去重：WG算法中搜索的空间实际上是由当前对象的状态和到达这个状态的operation集合来确定的。比如以一个寄存器模型为例，对于如下两个搜索路径：

path1: e1 e2 e3 -> register=10 ...
path2: e2 e3 e1 -> register=10 ...

假设我们在WG算法中，当前的搜索路径为：path1，执行过e1 e2 e3之后，寄存器的当前值变成了10，然后在继续往后搜索中的某一步失败了，重新回溯，现在到达了path2，执行e2 e3 e1之后，寄存器的值也变成了10。与path1相比，寄存器的当前值相同，同时达到这个状态的事件集合相同都是e1 e2 e3(只是执行顺序不同)，同时后续剩余的事件集合也肯定相同。此时实际上已经没有必要继续往下搜了，因为path1已经到达过这个状态，继续搜肯定也会失败。但是对于WG算法来说，它还是会继续搜索。

如果我们把所有曾经达到的状态(寄存器的值+到达这个值的事件集合)都记录下来，每次搜索的时候查找一下，如果发现事件集合和寄存器与之前记录的一致，那么就可以直接跳过了。WGL算法就是使用了这种动态规划的思想，通过记住之前搜索过的状态，避免重复性的搜索。

可以看出状态空间，从排列变成了组合，虽然有很大的降低，但依然是指数级的，复杂度依然很高。另外理论上已经证明，可线性化验证本身是一个NP完全问题。

3.并行化搜索。我们还可以把搜索时的路径选择方法变换一下，最简单的比如进行随机化。同时启动多个线程执行不同的搜索过程，只要有一个搜索到就可以结束了。Jepsen测试的线性化验证中，默认情况下就会启动两种算法去搜索来进行加速，这种模式实际上采用的竞争模式，每个线程需要搜索的总空间是相同的，只是把路径的选择方式进行变化。也可以采用合作模式，把整个搜索空间进行划分，每个线程负责一个子空间，同样只要有一个找到即可。或者采用竞争与合作混合的并行模式进行搜索，同一个子空间下再启动多个进行竞争模式的搜索。

3.3 P-compositionality*

线性一致性模型的locality属性：一个系统是线性一致的，当且仅当它所有的对象都是线性一致的。该属性的详细证明见论文2)，根据该属性，对于由多个对象的操作组成的一个History来说，如果它的每个对象都是线性一致的，那么这个系统就是线性一致的。这样我们在验证时，就可以把History按照对象进行分组，把同一个对象的放到一个组内，然后只要验证每个对象自己的History就可以了。这样可以大大降低元素History可线性验证的时间。

P-compositionality*中，P代表了partition，可以理解成是把History映射到多个子History的分区函数。P-compositionality*是对locality概念的推广，locality是P-compositionality*的一种特殊划分方法，它对应的划分方法就是按照对象对History(一个History中可以包含多个对象的操作)进行划分，每个对象的事件作为一个子集合。在论文2)的定义中，对象代表了一种数据类型，通常由一组可能的values和操作组成。比如一个set就是一个对象，支持insert/get/exsits操作，在论文2)里会将set作为一个对象考虑，而P-compositionality*则进一步地可以把set里面的一个key作为一个对象考虑。以set为例，如果我们关于set的某个约束在某个partition方式下，比如根据key对History进行划分，满足：set对象是可线性化的当且仅当它的每个key都是可线性化的，我们就说它是P-compositionality*的。这样就可以把关于一个set对象的所有操作组成的History，再根据key进行更细粒度的划分，这样就只需要对同一个key的操作组成的子History分别进行验证。

也就是说对于某些模型在某些特殊的约束条件下如果是满足P-compositionality*的，就可以把一个History按照对应的Partition方式分成多个子History，然后只要验证每个子History是可线性化的即可。相当于把复杂度中的n降低了。比如一个对象的History本来有100个事件，如果它满足P-compositionality*，通过partition就可以把它变成10个子集，每个只有10个事件，验证的事件数规模大大降低。

比如原始的History是关于set1和set2两个set对象的操作组成的：

set1 (insert 2)
set1 (ok)
set2 (insert 1)
set2 (ok)
set1 (get 1)
set1 (ok)
set2 (insert 3)
set2 (ok)

 对于这个History来说，它的事件个数是4。根据线性一致性模型本身具有的locality属性，我们可以把这个History根据set对象分成两个History分别验证，每个变成了2个事件。

----------------------- sub history 1
set1 (insert 2)
set1 (ok)
set1 (get 1)
set1 (ok)
----------------------- sub history 2
set2 (insert 1)
set2 (ok)
set2 (insert 3)
set2 (ok)

再根据set在按照key进行划分的情况下本身具有的P-compositionality*属性。可以继续按照每个set再按照key继续进行拆分如下：

----------------------- sub history 1
set1 (insert 2)
set1 (ok)
----------------------- sub history 2
set1 (get 1)
set1 (ok)
----------------------- sub history 3
set2 (insert 1)
set2 (ok)
----------------------- sub history 4
set2 (insert 3)
set2 (ok)

这样每个history需要验证的事件数就变成了1。

这个优化依赖于具体的数据模型是否存在满足P-compositionality*条件的一个约束和划分函数。

4 如何降低验证的复杂度

就算有如上的一些算法和优化，可线性化验证的复杂度在极端情况下仍可能是指数级的。实际进行Jepsen测试的时候，我们还可以通过如下途径来尽量降低验证的复杂度。

4.1 尽量减少timeout的Operation

线性一致性模型的nonblocking属性，允许一个事件只有invoke，没有response。对应到实际系统中，就是操作执行结果不确定，比如rpc调用timeout，对于这种情况我们不知道这个操作是成功还是失败。对于这种情况，在线性化验证过程中，会认为这个事件是在整个History结束之后才结束。这样这个事件就与发生在它的invoke之后的所有事件都是并行的，那么进行线性化验证时需要搜索的空间也随之变大。在极端情况下，如果所有操作都是timeout，那么所有的操作就都是并行的，整个验证复杂度是指数级的。

需要尽量减少这种操作timeout的情况。举例来说，我们可以把读请求的超时认为是失败，原因是读请求不影响系统的状态，而对于失败的操作来说，Jepsen在进行线性化验证时会直接忽略掉。

4.2 通过采用多个对象来增加并发

受限于线性化验证复杂度的影响，需要限制对于同一个对象的操作个数，这样意味着测试压力不能太大。而根据locality属性，对于针对多个对象的History我们可以按照对象划分，只需要分别验证每个对象的History是否是可线性化的。因此如果我们希望增加系统的压力，产生更多的操作，可以通过增加对象个数来实现。以寄存器模型来说，我们可以通过构造多个寄存器对象进行操作来实现。Jepsen测试框架中除了普通的register模型外，本身也提供了对multi-register模型的支持，用户可以直接使用。