看数据结构写代码（20）稀疏矩阵（顺序存储方式）

杂谈：昨天辞职了，告别了繁重又无意义的工作。准备在家专心学习数据结构,好好磨练自己的基本功。

在写这个小例子的时候遇到了 stack overflow(栈溢出）的问题，是 自己 分配了 过大的 栈变量，导致栈溢出。说实话，这还是 第一次 遇到，呵呵，别笑话我。看到网上的博客在 说这个问题，还提起一些 操作系统术语，自己还真是 一知半解。好好努力，打好基本功吧。骚年。

进入正题：

当矩阵 的 有用信息非常少时，我们考虑将矩阵压缩存储。这就涉及到 特殊矩阵 和 稀疏矩阵。

特殊矩阵 指的是 有一定规律的 矩阵，这个矩阵 我们 只存储 部分 有用信息，其余的信息 可以通过 公式 转换 求得。例如 对称矩阵，我们按行存储主对角线以下（包括主对角线）的元素，其余元素 我们可以通过 下面的公式求得。

稀疏矩阵，指的事没有一定规律的矩阵，并且  有用信息总数/矩阵总数 小于等于 0.05 的时候，我们称之为 稀疏矩阵。

稀疏矩阵的表示方式有三种：1.三元组 2. 行逻辑链接顺序表 3 .十字链表 

前两种 是 顺序的存储方式，第三种 是链表的存储方式。 

下面代码给出的 是行逻辑链接顺序表的方式，这种方式 只是 比 三元组的 方式 多 了 一个存放 每行首元素位置的数组，这样使矩阵在矩阵乘法 和 矩阵 加减法 带来了 很大的便利。

欢迎指出 代码 bug,下面上代码

// Sparse Matrix.cpp : 定义控制台应用程序的入口点。
//
//稀疏矩阵的顺序存储方式实现(行逻辑链接数据表）

#include "stdafx.h"

//#define MATRIX_MAX_SIZE	10000
//#define MATRIX_MAX_ROW	500
#define MATRIX_MAX_SIZE	100
#define MATRIX_MAX_ROW	50
enum E_State
{
	E_State_Error = 0,
	E_State_Ok = 1,
};
typedef int ElementType;

//矩阵元素结构
struct MatrixData
{
	int row;//行
	int col;//列
	ElementType data;//数据
};

struct SMatrix
{
	MatrixData base[MATRIX_MAX_SIZE];
	int rPos[MATRIX_MAX_ROW];//存储每行第一个元素在数组中的位置,并且保留了 最后一行的 边界值
	int rowNum;//行数
	int colNum;//列数
	int totalNum;//总数
};

void SMatrixInit(SMatrix * matrix,int * base,int row,int col){
	matrix->rowNum = row;
	matrix->colNum = col;
	int totalNum = 0;
	for (int i = 0; i < row; i++)
	{
		int lastRowTotal = totalNum;//记录从第一行到 上一行的总数
		for (int j = 0; j < col; j++)
		{
			ElementType data = base[i*col+j];
			if (data != 0)
			{
				matrix->base[totalNum].row = i;
				matrix->base[totalNum].col = j;
				matrix->base[totalNum].data = data;
				totalNum++;
			}
		}
		matrix->rPos[i] = lastRowTotal;
	}
	matrix->rPos[row] = totalNum;//为了 矩阵相乘，添加 边界条件
	matrix->totalNum = totalNum;
}

//普通转置 时间复杂度 O(m.colNum * m.totalNum)
//遍历矩阵m，将第一列到 最后 一列 的矩阵元素加入到 t矩阵中

void SMatrixTranspose(SMatrix m,SMatrix * t){
	t->totalNum = m.totalNum;
	t->rowNum = m.colNum;
	t->colNum = m.rowNum;
	int total = 0;
	for (int i = 0; i < m.colNum; i++)
	{
		for (int j = 0; j < m.totalNum; j++)
		{
			MatrixData data = m.base[j];
			if (data.col == i)
			{
				t->base[total].row = data.col;
				t->base[total].col = data.row;
				t->base[total].data = data.data;
				total++;
			}
		}
	}

}


//快速转置 时间复杂度为 O(m.totalNum + m.colNum)
void SMatrixQuickTranspose(SMatrix m,SMatrix * t){
	t->totalNum = m.totalNum;
	t->rowNum = m.colNum;
	t->colNum = m.rowNum;
	if (m.totalNum == 0)
	{
		return;
	}
	int col[MATRIX_MAX_ROW] = {0};
	for (int i = 0; i < m.totalNum; i++)//计算矩阵m 每一列 的 元素个数
	{
		MatrixData data = m.base[i];
		col[data.col+1]++;
	}
	//计算 矩阵M 每一列 起始元素 在数组中的位置
	for (int i = 1; i < m.colNum; i++)
	{
		col[i] = col[i-1] + col[i];
	}
	for (int i = 0; i < m.totalNum; i++)
	{
		MatrixData data = m.base[i];
		int colBase = col[data.col];
		t->base[colBase].col = data.row;
		t->base[colBase].row = data.col;
		t->base[colBase].data = data.data;
		col[data.col]++;
	}
	//最后设置 每行 首元素地址
	t->rPos[0] = 0;
	for (int i = 1; i < t->rowNum; i++)
	{
		t->rPos[i] = col[i-1];
	}

}

//矩阵相加
E_State SMatrixAdd(SMatrix m1,SMatrix m2,SMatrix * sum){
	if (m1.rowNum != m2.rowNum || m1.colNum != m2.colNum)
	{
		return E_State_Error;
	}
	int totalNum = 0;
	sum->rowNum = m1.rowNum;
	sum->colNum = m1.colNum;
	for (int i = 0; i < m1.rowNum; i++)
	{
		int m1Start = m1.rPos[i];
		int m1End = m1.rPos[i+1];
		int m2Start = m2.rPos[i];
		int m2End = m2.rPos[i+1];
		sum->rPos[i] = totalNum;
		while (m1Start < m1End && m2Start < m2End)
		{
			MatrixData m1Data = m1.base[m1Start];
			MatrixData m2Data = m2.base[m2Start];
			int m1Col = m1Data.col;
			int m2Col = m2Data.col;
			if (m1Col == m2Col)//相等
			{
				int sumData =m1Data.data + m2Data.data;
				if (sumData != 0)
				{
					sum->base[totalNum].row = i;
					sum->base[totalNum].col = m1Col;
					sum->base[totalNum].data = sumData;
					totalNum++;
				}
				m1Start++;
				m2Start++;
			}
			else if (m1Col < m2Col)//m2 的列 大
			{
				sum->base[totalNum].row = i;
				sum->base[totalNum].col = m1Col;
				sum->base[totalNum].data = m1Data.data;
				totalNum++;
				m1Start++;
			}
			else//m1的列大
			{
				sum->base[totalNum].row = i;
				sum->base[totalNum].col = m2Col;
				sum->base[totalNum].data = m2Data.data;
				totalNum++;
				m2Start++;
			}
		}
		while (m1Start < m1End)
		{
			MatrixData m1Data = m1.base[m1Start];
			int m1Col = m1Data.col;
			sum->base[totalNum].row = i;
			sum->base[totalNum].col = m1Col;
			sum->base[totalNum].data = m1Data.data;
			totalNum++;
			m1Start++;
		}
		while (m2Start < m2End)
		{
			MatrixData m2Data = m2.base[m2Start];
			int m2Col = m2Data.col;
			sum->base[totalNum].row = i;
			sum->base[totalNum].col = m2Col;
			sum->base[totalNum].data = m2Data.data;
			totalNum++;
			m2Start++;
		}
	}
	sum->rPos[sum->rowNum] = totalNum;
	sum->totalNum = totalNum;
	return E_State_Ok;
}

//矩阵相减

E_State SMatrixSub(SMatrix m1,SMatrix m2,SMatrix * sub){
	if (m1.rowNum != m2.rowNum || m1.colNum != m2.colNum)
	{
		return E_State_Error;
	}
	for (int i = 0; i < m2.totalNum; i++)
	{
		m2.base[i].data = -m2.base[i].data;
	}
	E_State state = SMatrixAdd(m1,m2,sub);
	return state;

}

//矩阵相乘
E_State SMatrixMult(SMatrix  m1,SMatrix  m2,SMatrix * result){
	if (m1.colNum != m2.rowNum)//排除不合法的情况..
	{
		return E_State_Error;
	}
	result->rowNum = m1.rowNum;
	result->colNum = m2.colNum;
	result->totalNum = 0;
	if (m1.totalNum * m2.totalNum != 0)
	{
		for (int m1Row = 0; m1Row < m1.rowNum; m1Row++)
		{
			int m1End = m1.rPos[m1Row+1];
			int colCount[MATRIX_MAX_ROW] = {0};
			for (int m1Start = m1.rPos[m1Row]; m1Start < m1End; m1Start++)
			{
				MatrixData m1Data = m1.base[m1Start];
				int col = m1Data.col;
				for (int m2start = m2.rPos[col]; m2start < m2.rPos[col+1]; m2start++)
				{
					MatrixData m2Data = m2.base[m2start];
					colCount[m2Data.col] += m1Data.data * m2Data.data;
				}
			}
			result->rPos[m1Row] = result->totalNum;
			for (int col = 0; col < m2.colNum; col++)
			{
				if (colCount[col] != 0)
				{
					result->base[result->totalNum].col = col;
					result->base[result->totalNum].row = m1Row;
					result->base[result->totalNum].data = colCount[col];
					result->totalNum ++;
				}
			}
		}
		result->rPos[result->rowNum] = result->totalNum;
	}
	return E_State_Ok;
}

//遍历矩阵
void SMatricTraverse(SMatrix matrix){
	int rowNum = 0;
	printf("--------------遍历开始------------------------\n");
	for (int i = 0; i < matrix.totalNum; i++)
	{
		MatrixData data = matrix.base[i];
		printf("%d行  %d列 : %d\n",data.row+1,data.col+1,data.data);
	}
	printf("--------------遍历结束------------------------\n");
}


int initData[5][10] = {
	{1,0,0,0,0,0,0,0,0,0},
	{0,0,2,0,0,0,0,0,5,0},
	{0,0,0,3,0,0,0,0,0,0},
	{0,2,0,0,0,0,0,0,0,0},
	{1,0,0,0,0,0,0,0,0,9},
};

int initAddData[5][10]= {
	{1,0,0,0,3,0,0,0,0,0},
	{0,0,2,0,4,0,0,0,5,0},
	{0,0,0,3,0,0,0,0,0,0},
	{0,2,0,0,2,0,0,0,0,0},
	{1,0,0,0,1,0,0,0,0,9},
};

int initData2 [10][2] = {
	{1,0},
	{0,0},
	{0,0},
	{0,0},
	{0,0},
	{0,6},
	{0,0},
	{0,0},
	{5,0},
	{0,0},
};

int _tmain(int argc, _TCHAR* argv[])
{
	SMatrix matrix;
	SMatrixInit(&matrix,(int *)initData,5,10);
	SMatricTraverse(matrix);
	printf("--------------普通转置-----------------------\n");
	SMatrix tMatrix;
	SMatrixTranspose(matrix,&tMatrix);
	SMatricTraverse(tMatrix);
	printf("--------------快速转置-----------------------\n");
	SMatrix qtMatrix;
	SMatrixQuickTranspose(matrix,&qtMatrix);
	SMatricTraverse(qtMatrix);
	printf("--------------矩阵相乘-----------------------\n");
	SMatrix m2;
	SMatrixInit(&m2,(int *)initData2,10,2);
	SMatrix mul;
	SMatrixMult(matrix,m2,&mul);
	SMatricTraverse(mul);
	printf("--------------矩阵相加-----------------------\n");
	SMatrix mAdd;
	SMatrixInit(&mAdd,(int *)initAddData,5,10);
	SMatrix mSum;
	SMatrixAdd(matrix,mAdd,&mSum);
	SMatricTraverse(mSum);
	printf("--------------矩阵相减-----------------------\n");
	SMatrix mSub;
	SMatrixSub(matrix,mAdd,&mSub);
	SMatricTraverse(mSub);
	return 0;
}

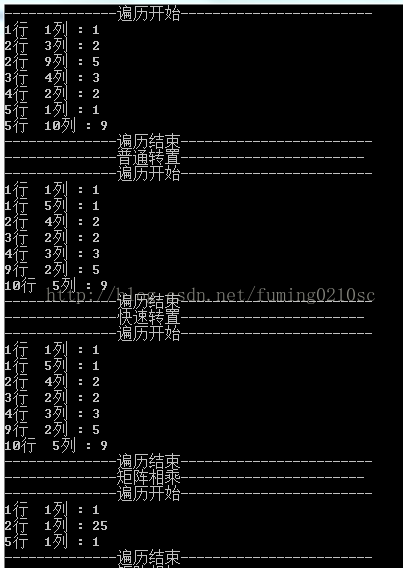
运行代码，截图